Теорема о верхней границе коэффициента использования ЦП

Теория планирования в реальном времени. Планирование периодических задач

Анализ производительности проекта параллельной системы

Анализ производительности проекта особенно важен для систем реального вре­мени. Если такая система не справляется со своими задачами в течение отведен­ного интервала, последствия могут быть катастрофическими.

Количественный анализ проекта системы реального времени позволяет на ранних этапах выявить потенциальные проблемы с производительностью. Ана­лизу подвергается проект ПО, концептуально исполняемый на данной аппарат­ной конфигурации с рассчитанной внешней рабочей нагрузкой. Обнаружив веро­ятные проблемы, легко рассмотреть альтернативные подходы к проектированию или иную конфигурацию аппаратуры.

В теории планирования в реальном времени рассматриваются вопросы приори­тетного планирования параллельных задач с жесткими временными ограничени­ями. В частности, она позволяет предсказать, будет ли группа задач, для каждой из которых потребление ресурсов ЦП известно, удовлетворять этим ограничени­ям. В теории предполагается использование алгоритма приоритетного планиро­вания с вытеснением.

По мере своего развития теория планирования в реальном времени применя­лась к все более сложным задачам, в числе которых планирование независимых периодических задач, планирование в ситуации, когда есть и периодические, и апериодические (асинхронные) задачи, а также планирование задач, требующих синхронизации.

Планирование периодических задач. Изначально алгоритмы планирования в реальном времени разрабатывались для независимых периодических задач, то есть таких периодических задач, кото­рые не взаимодействуют друг с другом и, следовательно, не нуждаются в синхро­низации. Периодическая задача характеризуется периодом Т (частота запуска) и вре­менем выполнения С (время ЦП, необходимое для завершения одного запуска). Коэффициент использования ЦП для нее равен U = С/Т. Задача называется пла­нируемой (schedulable), если она удовлетворяет всем временным ограничениям, то есть ее исполнение завершается до истечения периода. Группа задач именуется планируемой, когда планируемой является каждая входящая в нее задача.

Пользуясь теорией планирования, можно показать, что группа независимых пе­риодических задач всегда удовлетворяет временным ограничениям при условии, что сумма отношений С/Т по всем задачам меньше некоторого граничного значения.

Теорема о верхней границе коэффициента использования ЦП гласит:

Множество из п независимых периодических задач, планируемых согласно алго­ритму монотонных частот, всегда удовлетворяет временным ограничениям, если

где С_i и Т_i – время выполнения и период задачи t_i соответственно.

Верхняя граница U(n) стремится к 69% (ln 2), когда число задач стремится к бесконечности. Значения верхней границы для числа задач от 1 до 9 приведены в табл.11.1. Это оценка для худшего случая, но, как показано в работе [22], для случайно выбранной группы задач вероятная верхняя граница равна 88%. Если периоды задач гармоничны (являются кратными друг другу), то верхняя граница оказывается еще выше.

Обобщенная теорема о верхней границе коэффициента использования (теорема 4):

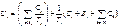
Здесь U_i – верхняя граница коэффициента использования ЦП за период Т_i для задачи t_i. Первый член в полученной формуле – суммарное использование за счет вытеснения высокоприоритетными задачами с периодом меньшим, чем у t_i. Второй член соответствует использованию процессора задачей t_i Третий член учитывает время блокировки задачи t_i в худшем случае, а четвертый – суммарное время вытеснения этой задачи более приоритетными, но с периодами меньшими, чем у t_i.

Достоинство алгоритма монотонных частот заключается в том, что он сохра­няет устойчивость в условиях краткосрочной перегрузки.

Дата добавления: 2014-01-07