Строгая формулировки теоремы о времени завершения

Теорема о времени завершения.

Если для некоторого множества задач полный коэффициент использования больше, чем требует теорема о верхней границе, то можно прибегнуть к помощи теоремы о времени завершения

Теорема о времени завершения (теорема 2) гласит:

Если имеется такое множество независимых периодических задач, в котором каждая задача успевает завершиться вовремя в случае, когда все задачи запуска­ются одновременно, то все задачи смогут завершиться вовремя при любой комби­нации моментов запуска.

Чтобы убедиться в выполнении условий теоремы, необходимо проверить мо­мент завершения первого периода для данной задачи t_i, а также моменты завер­шения периодов всех задач с более высоким приоритетом. Согласно алгоритму монотонных частот, периоды подобных задач будут меньше, чем для задачи t_i. Эти периоды называются точками планирования. Задача t. один раз займет ЦП на вре­мя С_i в течение своего периода Т_i. Но более приоритетные задачи будут выпол­няться чаще и могут по крайней мере один раз вытеснить t_i. Поэтому нужно учесть также время ЦП, затраченное на более приоритетные задачи.

Теорема о времени завершения графически представляется с помощью вре­менной диаграммы, на которой показана упорядоченная по времени последова­тельность выполнения группы задач.

Теорему о времени завершения можно строго сформулировать следующим образом: Множество независимых периодических задач, планируемых согласно алгорит­му монотонных частот, будет удовлетворять временным ограничениям при любой комбинации моментов запуска тогда и только тогда, когда

,

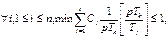
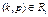где С_i и Т_i – время выполнения и период задачи t_j соответственно, а

R_i = {(k,p): l≤k≤i, p=l,...,[T_i/T_k]}.

В этой формуле t_i – это проверяемая задача, a t_k – любая из более приоритетных задач, влияющих на время выполнения t_i. Для данной пары задач t_i и t_k каждое зна­чение р представляет некоторую точку планирования задачи t_k. В каждой точке планирования необходимо рассмотреть один раз время ЦП С_i, потраченное на зада­чу t_i, а также время, израсходованное на более приоритетные задачи. Это позволит определить, успеет ли t_i завершить выполнение к данной точке планирования.

Дата добавления: 2014-01-07