I. Предмет и методы статистической науки

Вопросы к зачету (экзамену) по статистике

1. Предмет и методы статистической науки.
2. Основные понятия и категории.
3. Методы статистики.
4. Сводка и группировка статистических данных.
5. Сводка. Основные виды сводок.
6. Статистическая группировка.
7. Классификация статистических группировок.
8. Основные этапы построения статистических группировок.
9. Интервалы группировки.
10. Ряды распределения.
11. Классификация рядов распределения.
12. Абсолютные и относительные величины.
13. Средние величины.
14. Структурные средние.

1). Основные понятия и категории

2). Методы статистики

Статистика связана со счетом каких-либо объектов и с определением их количественных характеристик.

Основные понятия статистики:

1). Статистика – это статистические данные, публикуемые в печати.

2). Статистика – это планомерный и систематический учет массовых общественных явлений, которые осуществляются статистическими органами.

3). Статистика – это самостоятельная научная дисциплина.

Общее понятие статистики – самостоятельная общественная наука, изучающая количественную сторону массовых общественных явлений вне разрывной связи с их качественной стороной, конкретных условиях места и времени, с целью выявления присущих этим явлениям тенденций и закономерностей развития.

1). Статистика это наука – так как имеет самостоятельный предмет изучения и специфический метод исследования этого предмета. Предметом исследования являются общественно-экономические явления.

2). Статистика наука общественная, а не универсальная.

3). Статистика изучает массовые общественные явления, а не единичные факты. Конечной целью любого статистического исследования является выявление тенденций и закономерностей развития. Задача любого статистического исследования – совокупность как можно большего количества повторов.

4). Статистика изучает количественную сторону общественных явлений, которые выражаются в том, что им присущи – размеры, объемы, пропорции, соотношения и т.д., которые существуют объективно вне зависимости от того, находят ли они свое выражение в статистических показателях или нет.

5). Статистика изучает количество определенного качества.

6). Статистика изучает социально-экономические явления, в конкретных условиях, месте и времени. Пространственно-временная определенность статистических показателей является спецификой статистики.

Основные понятия и определения

Объектом статистики – выступают массы однородных в качественном отношении явлений и процессов называющиеся статистическими совокупностями (статистические совокупности – исходная категория статистики)

Единицей статистической совокупности являются отдельно взятые элементы, которые характеризуются качественной однородность, внутренней связью и внешней независимостью.

Признак – это отличительная особенность, черта изучаемого явления или процесса.

Все признаки делятся на:

1). Количественные и качественные.

2). Стабильные и варьирующие.

3). Факторные и результативные.

Количественный – это признак, который имеет числовое выражение.

Качественный – это признак, который характеризует некое состояние единицы совокупности и числом не выражается. Если качественные признаки представлены двумя противоположными значениями, то они называются альтернативными.

Стабильный признак – не изменяется ни во времени, ни в пространстве.

Результативный – это признак, который изменяется под воздействием факторов.

Факторные – это признаки, которые оказывают влияние на изменение факторов.

Измеренные количественный характеристики изучаемых явлений статистика выражает в категории – статистические показатели.

Статистический показатель – обобщенная количественная характеристика социально-экономических явлений и процессов в их качественной определенности в условиях конкретного места и времени.

Статистические показатели бывают:

1) Количественные

2) Качественные

Измеряя объем статистической совокупности и определяя численность единиц, обладающих тем или иным признаком, статистика получает количественные показатели.

Количественная характеристика уровня степени распространенности явления и процесса измеряется качественными показателями.

Совокупность показателей, всесторонне отражающие сложное социально-экономическое явление, составляют систему показателей.

Статистическая закономерность предопределяет типичное распределение единиц статистического множества на определенный момент времени под воздействием всей совокупности факторов и является объективной количественной закономерностью массового процесса.

Статистическое исследование состоит из трех стадий:

1). Статистическое наблюдение

2). Сводка и группировка данных

3). Анализ данных

Статистическое изучение социально-экономических явлений начинается с элементов статистического множества. Планомерная и систематическая регистрация существующих признаков у единиц статистической совокупности составляют основу статистического наблюдения.

На данной стадии формируется массив исходных данных различными способами:

1). Отчетность

2). Анкетный способ

3). Экспедиционный способ

Сбор информации – полученные после статистического наблюдения массивы данных нуждаются в обработке, которая составляет суть сводки и группировки данных наблюдения.

Выявление совокупности однородных групп называются – группировки. На этой стадии производится суммирование величин отдельных признаков по типическим группам и вычисления абсолютных, относительных и средних величин.

Относительные и средние величины в статистике называются обобщающими показателями, так как они уравнивают индивидуальные особенности и устраняют случайные колебания.

Анализ – производится расчет статистических показателей, характеризующих структуру, вариацию, взаимосвязь, динамику социально-экономических явлений.

В своем конкретном проявлении статистический метод распадается на ряд частных методов:

1). Табличный.

2). Графический

3). Метод Группировок

4). Метод Средних величин

5). Показатели вариаций

6). Корреляционный метод

7). Регрессионный метод

8). Индексный метод

9). Метод анализа рядов динамики и т.д.

Особенности курса «Статистика»:

1). Вырабатывает специфические статистические категории. Определяет их сущность, значение и основные принципы работы с ними.

2). Разрабатывает систему сбора, обработки и анализа статистических данных, то есть разрабатывает статистическую методологию.

3). Выступает как абстрактная наука, которая рассматривает отвлеченные понятия, несвязанные с конкретными явлениями или процессами.

4). Является методологической наукой, которая разрабатывает методы, приемы исследования социально-экономических явлений и показывает их возможности в анализе и конкретных условиях применения.

Сводка и группировка статистических данных

1). Сводка. Основные виды сводок

2).Статистическая группировка. Классификация статистических группировок

3). Основные этапы построения статистических группировок

4). Ряды распределения. Классификация рядов распределения

Сводка – научная обработка первичных данных с целью получения обобщенных характеристик изучаемого явления по ряду существенных для него признаков. В статистике различают:

1). Сводку простую и сложную

2). Сводку централизованную и децентрализованную

3). Сводку ручную и механизированную

Простая сводка – операция по подсчету итоговых и групповых данных и оформление результатов этой работы в виде статистических таблиц.

Сложная сводка – охватывает группировку полученных при наблюдении статистических данных, составление системы показателей для характеристики типичных групп и подгрупп изучаемой совокупности явления, подсчет числа единиц в группах и подгруппах, и оформление результатов этой работы в виде статистических таблиц.

Сводка централизованная – данные остаются в организации, в которую информация сдана.

Сводка децентрализованная – данные направляются в другие организации (вышестоящие).

Статистическая группировка

Статистическая группировка – разбиение (расчленение) общей совокупности единиц объекта наблюдения по одному или нескольким существенным признакам на однородные группы, различающиеся между собой по социально-экономическим типам и позволяющие определить структуру совокупности изучить взаимосвязи и взаимозависимости между явлениями и признаками их характеризующими, а также определить классы типичные для изучаемой совокупности.

Статистическая группировка по характеру решения задач бывает:

1). Типологическая

2). Структурная

3). Аналитическая

Типологическая группировка – разбиение разнородной совокупности единиц объекта наблюдения на качественно однородные группы (строится в натуральных величинах)

Структурная группировка – решает задачи изучения структуры совокупности (строится в процентах)

Аналитическая – позволяет выявить взаимосвязи между явлениями и признаками их характеризующими.

Особенностями построения являются:

1). В качестве группировочного всегда выступает факторный признак.

2). Каждая выделенная группа характеризуется средним значением результативного признака.

По способу построения группировки бывают:

1). Простые

2). Комбинационные

Простая группировка – построенная по одному признаку.

Комбинационная группировка – это группировка, построенная по двум и более признакам.

Этапы построения группировок

1). Выбор группировочного признака

2). Определение числа групп

3). Определение числа интервала

4). Определение признаков, которые в комбинации друг с другом наиболее полно характеризуют каждую выделенную группу.

1).Группировочным называется признак, по которому осуществляется разбиение единиц совокупности на группы. В качестве группировочного может выступать как количественный, так и качественный признаки.

2). Определение числа групп.

Число групп зависит:

- от вида показателя, положенного в основание группировки

- от объема изучаемой совокупности

- от степени вариации признака

- от цели исследования

(группы содержащие менее 10 единиц к анализу НЕ ПРИНИМАЮТСЯ)

Способ определения числа групп:

а). Если анализируется совокупность достаточно большого объема (от 50 единиц наблюдения), то число групп определяется по формуле Стэрджеса

n=1+3,322lgN

n – число групп

N – объем совокупности

б). Если анализируется совокупность малого объема (мене 50 единиц наблюдения), то число группировок должно быть в 6-7 раз меньше объема изучаемой совокупности.

3). Определение интервалов (ширины) группировки.

Интервалы группировки бывают:

а). Равные и неравные

б). Открытые и закрытые

Равные – это интервалы, в которых ширина интервала от интервала к интервалу составляет одно и тоже число.

Неравные – возникают при объединении некоторых интервалов, в случае отсутствия показателей...

Закрытые – это интервалы, в которых существует и верхняя и нижняя границы.

Открытые – интервалы, в которых отсутствует одна из границ: как правило нижняя у первого интервала и верхняя у последнего.

Ширина равного интервала определяется

X max – X min

H = n

Х max – максимальное значение признаков совокупности

X min – минимальное значение признаков совокупности

n - число групп

При определении ширины интервала производится округление в большую сторону.

Ряды распределения

Ряд распределения – это количественное распределение единиц совокупности по одному или нескольким существенным признакам в зависимости от того, какой признак положен в основании группировки. Ряды распределения бывают:

1). Атрибутивные

2). Вариационные

Атрибутивный – ряд распределения, построенный по качественному признаку, то есть признаку не имеющему числового выражения

Вариативный - ряд распределения, построенный по качественному признаку, то есть признаку имеющему числовое выражение.

Вариационные ряды распределения бывают:

1). Дискретные

2). Интервальные

Дискретный вариационный ряд распределения - это ряд, в котором признак изменяется прерывно, то есть на конкретное число единиц.

Интервальный вариационный ряд распределения – это ряд, в котором признак в интервале может принимать любые значения

Вариационные ряды распределения состоят из двух элементов:

1). Признака – X(i)

2). Частоты – F (i), которая показывает, как часто то или иное значение признака встречается в совокупности.

Абсолютные и относительные величины

Статистические показатели («величины») в статистике подразделяются на:

1). Абсолютные

2). Относительные

3). Средние

Абсолютные величины характеризуют количественную сторону сущности явления, имеют определенную размерность, являются основанием для расчета относительных величин и могут быть измерены в натуральном, стоимостном и трудовом выражении.

Относительные величины – это показатели, которые выражают количественные соотношения между социально-экономическими явлениями и признаками их характеризующими. Относительные величины получаются в результате деления двух абсолютных величин.

Величина, с которой производится сравнение называется «основанием», «базой сравнения», «базисной величиной».

Величина, которая сравнивается называется «текущей», «сравниваемой», «отчетной величиной».

В результате сопоставления одноименных абсолютных величин получается величина не имеющая размерности.

В результате сопоставления разноименных величин, получается относительная величина, принимающая наименование и числителя, и знаменателя.

Различают 8 видов относительных величин:

1). Относительная величина планового задания (ОВПЗ)

2). Относительная величина выполнения плана (ОВВП)

3). Относительная величина структуры (ОВС)

4). Относительная величина координации (ОВК)

5). Относительная величина динамики (ОВД)

6). Относительная величина интенсивности (ОВИ)

7). Относительная величина уровня экономического развития (ОВУЭР)

8). Относительная величина сравнения (Овс)

Относительная величина планового задания представляет собой соотношение величины показателя, устанавливаемой на планируемый период к величине показателя, достигнутой к планируемому периоду или к периоду, принятому за базу сравнения.

Выражается в коэффициентах или процентах после дополнительного домножения на 100%.

Показывает на сколько процентов планируют больше или меньше того, что достигнуто к плановому периоду.

Относительная величина выполнения плана соотносится:

Фактический уровень показателя

ОВВП = Плановый уровень показателя

Выражается в коэффициентах или процентах после дополнительного домножения на 100%. Относительная величина структуры представляет собой соотношение частей и целого, характеризует структуру совокупности.

Выражается в долях единиц или процентах, рассчитанные по одной совокупности. В сумме относительная величина структуры составляет 1 или 100%.

Относительные величины координации представляют собой соотношение частей целого между собой.

Выражаются в долях единиц (допускается домножение на 10, 100 (если этого требует логика – не может быть соотношение людей 1 к 1,5, может 10 к 15...)

Относительная величина динамики характеризует изменение явления во времени, в результате получается величина не имеющая наименования. В зависимости от того, что принимается за базу сравнения, различаются относительные величины динамики:

1). Цепные

2). Базисные

Относительные величины динамики цепные – представляют собой соотношение текущей величины к величине показателя предыдущего периода. Показывает, как изменяется показатель от периода к периоду на протяжении рассматриваемого ряда динамики.

Относительная величина динамики базисная – представляет собой соотношение значения показателя текущего периода к величине показателя, принятого за базу сравнения.

Относительная величина интенсивности соотносится:

Величина показателя, степень распространения которого изучается

ОВИ = Среда, в которой происходит распространение явления

(Пример – плотность населения страны, число врачей на 1000 человек и т.д.)

Относительная величина уровня экономического развития – характеризует размеры производства различных видов продукции на душу населения. В знаменателе фигурирует «душа» - среднегодовая численность населения.

Относительная величина сравнения представляет собой соотношение одноименных величин, характеризующих разные объекты.

Задача по теме: прирост выпуска продукции отрасли по плану на 2005 год должен составить 7,5 %. Фактический рост составил 109,5 %. Определить относительную величину выполнения плана по выпуску продукции.

1). 109,5 /107,5 = 1,02

2). 1,02х100 = 102 %

Средние величины

1). Основные виды и формы средних величин. Среднеарифметическая.

2). Структурная средняя мода, медиана, квартили.

Средняя величина – обобщенная характеристика совокупности по признаку. Сущность средней величины заключается в том, что в ней учитываются отклонения, вызванные влиянием факторов основных существенных и нивелируются отклонения, вызванные влиянием случайных, второстепенных факторов.

В статистике различают следующие виды средних величин:

1). Средняя арифметическая

2). Средняя квадратическая

3). Средняя геометрическая

Все перечисленные средние величины могут быть представлены в двух формах:

1). Простой (не взвешенной)

2). Взвешенной

Простая форма средних применяется в случае, если расчет ведется по не сгруппированным данным, то есть данным представленными индивидуальными значениями признака.

Средние взвешенные применяются в случае, если расчет ведется по сгруппированным данным, то есть данным представленным в виде дискретного или интервального вариационного ряда распределений.

При расчете средних величин необходимо первоначально определять исходные соотношения средней или логическую формулу ее построения. Исходное соотношение средней представляет собой соотношение общего объема совокупности по признаку к общему объему совокупности по числу единиц наблюдения.

Если расчет ведется по не сгруппированным данным и при этом определены значения числителя и знаменателя исходного соотношения средней, то используется средняя арифметическая простая не взвешенная:

x – средняя

xi – значение признака

n – объем совокупности (число единиц наблюдения)

Если расчет ведется по сгруппированным данным, то используется формула средней арифметической взвешенной:

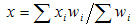
• — цена за единицу продукции; (значение признака)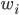
• — количество (объем) продукции;

Структурные средние

Мода (Мо) – это значение признака наиболее часто встречающиеся в совокупности. В зависимости от того, как представлены исходные данные, мода определяется:

1). Если исходные данные представлены в виде дискретного вариационного ряда распределения, то модальным будет признано значение, которому соответствует наибольшая частота.

2). Если исходные данные представлены в виде интервального ряда распределения, то мода определяется по формуле:

Мо =	Хо+ h* fmo – fmo-1 (fmo-fmo-1) + (fmo-fmo+1)

Xo – нижняя граница модального интервала (модальным называется интервал, которому соответствует наибольшая частота)

h – ширина модального интервала

fmo - частота модального интервала

fmo-1 – частота интервала, предшествующего модальному

fmo+1 – частота интервала, последующего за модальным

Медиана (Ме) – значение признака, находящееся в середине ранжированного ряда и делящая ряд на две, приблизительно равные части. В зависимости от того, как представлены исходные значения признака медиана определяется:

1). Если исходные данные представлены в не сгруппированном виде, то медианным будет являться значение, находящееся строго в середине упорядоченной совокупности единиц наблюдения по признаку в порядке возрастания или убывания.

(Мода чаще всего используется при оценке рынка товаров и услуг, медиана – при анализе экспертной информации)

2). Если исходные данные представлены в виде дискретного ряда распределения, то медианой будет являться значение – первая накопленная частота, которая превышает половину объема совокупности.

Дата добавления: 2014-01-07