Средняя арифметическая. Среди параметрических средних следует выделить три : среднюю арифметическую

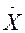Среди параметрических средних следует выделить три: среднюю арифметическую. среднюю гармоническую и среднюю геометрическую. Средняя арифметическая рассчитывается по первичному или вторичному, но прямому признаку. При этом, если признак первичный расчет должен проводится по формуле средней арифметической простой: , где - средняя арифметическая простая, 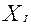- меняющееся от одной единицы к другой значение первичного признака, 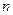- число таких значений. 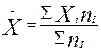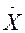Если признак вторичный расчет средней арифметической по нему ведется по формуле средней арифметической взвешенной , где - средняя арифметическая взвешенная, 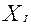- меняющееся значение вторичного признака,

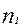- значение первичного признака, через который вторичный характеризует единицу совокупности (частота встречаемости вторичного признака); 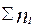- сумма частот. При расчете средней арифметической в дискретной вариационном ряду используется формула средней арифметической взвешенной, но если эта средняя считается по первичному признаку, то речь идет о «псевдо взвешенной» средней, поскольку дискретный ряд по такому признаку легко преобразовать в ранжированный и соответственно вести расчет средней по формуле средней простой.При расчете средней арифметической в интервальном вариационном ряду используется формула средней арифметической взвешенной, при этом в качестве 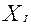берется середина каждого интервала, а качестве 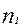- частота интервала. И в этом случае, если признак первичный, то речь идет о псевдо взвешенной средней

Средняя арифметическая обладает следующими математическими свойствами: 1) если каждое значение признака увеличить или уменьшить на некоторую постоянную величину а, средняя арифметическая соответственно увеличится или уменьшится на эту величину; 2) если каждое значение признака увеличить или уменьшить в одно и тоже число К раз, средняя арифметическая возрастет или уменьшится в это же число К раз; 3) если частоты по каждому значению признака увеличить или уменьшить в одно и то же число М раз, то величина средней арифметической не изменится.; 4) сумма отклонений всех значений признака от средней арифметической равна 0 (нулю), то есть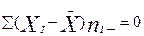

Для качественного альтернативного признака его среднее значение равно доле единиц определенного качества, то есть ,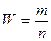

где m - число единиц в совокупности, обладающих неким качеством, n - общая численность совокупности

Дата добавления: 2014-01-07