
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способы формирования выборочной совокупности
|
|
|
|
Модульная единица 4
Резюме по модульной единице 3
Вопросы для повторения по модульной единице 3
7-1.Чему равен коэффициент вариации признака по выборочной совокупности, если предельная ошибка равна 2, генеральная средняя находится в интервале от 38.0 до 42.0, а выборочная дисперсия 16?
7-2.Как определить границы генеральной средней с заданной вероятностью?
7-3. Как определить границы генеральной доли?
7-4.При использовании каких выборок (больших или малых) границы генеральной средней будут шире?
7-5.Какова вероятность того, что генеральная средняя окажется вне установ- ленных границ?
7-6.Каков смысл необходимой численности выборки?
7-7.В каком случае можно определить необходимую численность выборки?
7-8.В каком случае следует определять вероятность появления ошибки?
Знакомство с основными типами задач, решаемых на основе выборочного метода позволяет решать вопросы, встречающиеся при использовании данного метода на практике.
Равновозможность (равновероятность) каждой единицы генеральной совокупности попасть в выборку обеспечивается, как уже говорилось ранее, различными способами отбора. Среди них следует выделить наиболее часто используемые: собственно случайный (повторный и бесповторный), механический, типический, серийный.
4.1 Собственно случайный отбор. При этом способе отбора каждой единице генеральной совокупности предварительно присваивается некоторая «метка» в виде числа, буквы и так далее, при этом «метка» никаким образом не должна быть связана с изучаемым признаком. Затем используя различные приемы, обеспечивающие случайность отбора (таблица случайных чисел, лототрон) осуществляется отбор «меток», как заменителей единиц.
Собственно случайный отбор проводится как повторный и как бесповторный.
При повторном отборе единицы генеральной совокупности, попавшие в выборку, после фиксации по ним значения признака, возвращаются обратно в генеральную совокупность, вследствие чего генеральная совокупность по численности остается постоянной, а, следовательно, вероятность попадания каждой единицы генеральной совокупности в выборку остается неизменной. Ранее рассмотренные алгоритмы для расчета средней и предельной ошибок, необходимой численности выборки исходят именно из этого способа формирования выборочной совокупности.
При бесповторном отборе единица генеральной совокупности, попавшая в выборку, в генеральную совокупность не возвращается, поэтому генеральная совокупность по численности уменьшается, а,следовательно, каждая последующая единица генеральной совокупности имеет возрастающую вероятность попасть в выборку. При бесповторном отборе при расчете средней, а, следовательно, и предельной ошибки вводится поправка на конечность генеральной совокупности (пкс) = . При больших значениях N единицей в знаменателе можно пренебречь и поправка на конечность совокупности будет выглядеть так: (пкс) =
. При больших значениях N единицей в знаменателе можно пренебречь и поправка на конечность совокупности будет выглядеть так: (пкс) = , следовательно, алгоритмы расчета средней и предельной ошибок выборочной средней при бесповторном отборе будут такими:
, следовательно, алгоритмы расчета средней и предельной ошибок выборочной средней при бесповторном отборе будут такими: 
 ;
;  . Множитель
. Множитель  < 1, вследствие чего, средняя ошибка и предельная ошибки при бесповторном отборе всегда меньше, чем при отборе повторном. Аналогичным образом, то есть с введением поправки
< 1, вследствие чего, средняя ошибка и предельная ошибки при бесповторном отборе всегда меньше, чем при отборе повторном. Аналогичным образом, то есть с введением поправки  меняются формулы для расчета средней и предельной ошибок для доли и других оценок.
меняются формулы для расчета средней и предельной ошибок для доли и других оценок.
4.2 Механический отбор используется в том случае если единицы генеральной совокупности объективно располагаются в каком либо порядке во времени или в пространстве или же есть возможность это сделать. Важно отметить, что порядок расположения единиц не должен быть связан с изучаемым явлением. С такого рода совокупностями можно встретиться, например, при социологических обследованиях, когда изучаемую совокупность людей можно расположить в алфавитном порядке или в зависимости от номера их стационарного телефона.
Для осуществления отбора находят отношение 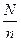 , получившее название шага или интервала отбора. Из совокупности, предварительно упорядоченной в указанном выше порядке, через найденный шаг осуществляется отбор (формирование выборки).
, получившее название шага или интервала отбора. Из совокупности, предварительно упорядоченной в указанном выше порядке, через найденный шаг осуществляется отбор (формирование выборки).
При механическом отборе расчет средней и предельной ошибок осуществляется по формулам случайного бесповторного отбора, поскольку механический отбор осуществляется как бесповторный.
4.3 Типический отбор целесообразно использовать в том случае, если в генеральной совокупности реально имеются своеобразные группы единиц (например, партии сена с разными сроками заготовки, группы животных на откорме разного возраста), или же такие группы можно выделить
(например группы коров с разным месяцем лактации).
Установив наличие в совокупности качественно отличных частей
(групп), далее определяется представительство каждой из этих частей в выборке. Представительство групп в выборке чаще всего устанавливается пропорционально их численности, то есть исходя из равенства  , где
, где 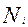 - численность i-ой группы в генеральной совокупности, представительство которой в выборке надо определить;
- численность i-ой группы в генеральной совокупности, представительство которой в выборке надо определить;  - общая численность генеральной совокупности;
- общая численность генеральной совокупности; 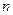 - общая численность выборки;
- общая численность выборки; 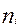 - искомая величина, то есть сколько единиц должно быть взято из i- ой группы в выборку. Из этого равенства следует, что
- искомая величина, то есть сколько единиц должно быть взято из i- ой группы в выборку. Из этого равенства следует, что 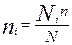 . Иногда представительство групп в выборке определяют пропорционально средним квадратическим отклонениям изучаемого признака в выделенных группах генеральной совокупности, пропорционально дисперсиям или объемам вариации. После определения представительства производится отбор из групп, при этом используется или случайный бесповторный или механический отбор. Поскольку типический отбор предполагает представительство в выборке всех качественно отличных групп генеральной совокупности, при расчете средней, а, соответственно, предельной ошибок учитывается колеблемость признака только внутри групп, то есть
. Иногда представительство групп в выборке определяют пропорционально средним квадратическим отклонениям изучаемого признака в выделенных группах генеральной совокупности, пропорционально дисперсиям или объемам вариации. После определения представительства производится отбор из групп, при этом используется или случайный бесповторный или механический отбор. Поскольку типический отбор предполагает представительство в выборке всех качественно отличных групп генеральной совокупности, при расчете средней, а, соответственно, предельной ошибок учитывается колеблемость признака только внутри групп, то есть 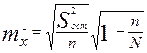 , а
, а 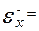
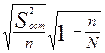 . Поскольку остаточная (средняя групповая дисперсия) составляет лишь часть общей дисперсии, типический отбор обеспечивает при прочих равных условиях минимальную по сравнению с другими способами отбора ошибку.
. Поскольку остаточная (средняя групповая дисперсия) составляет лишь часть общей дисперсии, типический отбор обеспечивает при прочих равных условиях минимальную по сравнению с другими способами отбора ошибку.
4.4 При серийном (гнездовом) отборе выборка формируется из серий (гнезд), состоящих из нескольких единиц. Например, при выборочном социологическом опросе доярок в качестве гнезда может выступать ферма, на которой,в случае попадания ее в выборку, будут опрошены все доярки. Отбор гнезд производится, как правило, механически. При расчете ошибок учитываются только межсерийные различия, следовательно, формулы для расчета средней и предельной ошибок для выборочной средней имеют вид: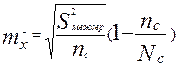 , а
, а 
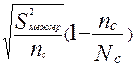 , где
, где 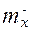 и
и 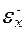 соответственно средняя и предельная ошибки выборочной средней,
соответственно средняя и предельная ошибки выборочной средней, 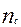 и
и  - число серий (гнезд) соответственно в выборочной и генеральной совокупностях;
- число серий (гнезд) соответственно в выборочной и генеральной совокупностях;  межсер - межсерийная дисперсия.
межсер - межсерийная дисперсия.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 678; Нарушение авторских прав?; Мы поможем в написании вашей работы!