Модульная единица 1

Рассматриваемые вопросы

1. Критерий как критерий согласия

2. Критерий как критерий независимости

3. Критерий как критерий однородности

Критерий как критерий согласия

Цель и задачи изучения модульной единицы

В результате изучения данного аспекта использования критерия студент должен закрепить общую схему проверки статистических гипотез уяснить алгоритм расчета фактического значения критерия и особенности нахождения его табличного значения.

Одним из важнейших типов статистических гипотез являются гипотезы о распределении численности. Предпочтение при проверке такого рода гипотез должно отдаваться критерию - Пирсона. Данный критерий является параметрическим. Важнейшим условием применения этого критерия является независимость наблюдений по группам (интервалам). Кроме того, имеется чисто количественное ограничение, состоящее в том, что в каждом интервале должно быть не менее 5 (пяти) единиц наблюдений. Если число наблюдений меньше 5, этот интервал следует объединить с соседним. Объединение производят до тех пор пока в объединенном интервале будет не менее 5 единиц. Критерий используется в 3-х аспектах (вариантах) – как критерий согласия, как критерий независимости и как критерий однородности. Как критерий согласия критерий используется в том случае, если требуется проверить гипотезу о соответствии фактического распределения теоретическому (ожидаемому).

Последовательность проверки гипотез о распределении численностей с использованием критерия в аспекте согласия рассмотрим на примере

Имеются выборочные данные о распределении коров определенной породы по жирности молока (в таблице 5.1.1 это фактические численности). Требуется установить соответствует ли распределение коров всей породы (в генеральной совокупности) по жирности молока пропорции 1:2:4:2:1

Таблица 5.1.1

К проверке гипотезы о соответствии фактического распределения коров по жирности молока ожидаемому

Этапы расчета критерия	Формула расчета	Процент жира в молоке
до 3.40	3,40-3,50	3,51-3,60	3,61-3,70	Свыше 3,70
Фактические численности	ni
Ожидаемые численности	ñi
Разности	ni - ñi	+4	-12	-17	-4	+29
Квадрат разности	(ni - ñi)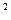
Отношение	(ni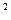 - ñi)/ ñi	0,16	0,72	0,72	0,08	8,41

В соответствии с общей схемой проверки гипотез на первом этапе выдвигаются две противостоящие друг другу гипотезы: Н0 (нулевая гипотеза) – распределение коров по жирности молока соответствует ожидаемой пропорции 1:2:4:2: 1 и НА (альтернативная гипотеза) распределение коров обозначенной пропорции не соответствует. Такая постановка нулевой гипотезы связана с тем, что распределение таково, что вероятность появления значений соответствующих альтернативной гипотезе весьма незначительна. В конечном счете должна быть признана справедливой одна из этих гипотез, а вторая, соответственно отвергнута.

В качестве критерия для проверки выдвинутых гипотез можно использовать параметрический критерий , поскольку наблюдения по группам независимы друг от друга.

Далее следует установить уровень значимости (α)и соответственно 1- α = β -достоверность вывода. Примем для нашего примера α=0,01 и =0,99

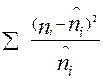На третьем этапе необходимо рассчитать фактическое значение критерия по формуле: факт = , где 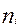- фактические численности по группам (интервалам) 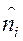- ожидаемые численности, причем в качестве ожидаемых берутся численности соответствующие нулевой гипотезе (Н0), то есть численности соответствующие пропорции 1:2:4:2:1

В таблице 5.1.1 представлены последовательные этапы расчета фактического значения критерия , при этом ожидаемые численности устанавливались следующим образом: определялась общая численность выборки (1000 голов) затем эта общая численность разбивалась по группам в пропорции 1:2:4:2:1. исходя из того, что на одну часть приходится 1000:10 = 100 единиц (голов). В целом же, при проверке гипотезы о соответствии фактического распределения ожидаемому, ожидаемые частоты следует определять умножая последовательно общую численность выборки на теоретическую вероятность появления тех или иных значений признака, по которому построено распределение.

Фактическое значение критерия определим суммируя отношения

(ni - ñi)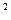/ ñi по последней строке таблицы факт = 0,16+0,72+0,72+0,08 +8,41 = 10,09.

На заключительном этапе проверки статистических гипотез фактическое значение критерия необходимо сравнить с его табличной (критической) величиной. В нашем примере табл определяется принятым уровнем значимости (α=0,01) и числом степеней свободы, которое при данном аспекте применения критерия равно df(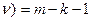, где = 5 – число интервалов (групп), k- число параметров определяющих теоретическое (ожидаемое) распределение. Поскольку в нашем примере ожидаемое распределение носит опытный характер k=0 число степеней свободы будет равно df(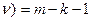= 5-1 =4, Следовательно, табл=13,28. Поскольку фактическое значение критерия (10,09) оказалось меньше табличного (13.28) справедливой должна быть признана нулевая гипотеза – с вероятностью ошибки в 1% распределение коров данной породы по жирности молока соответствует пропорции 1: 2:4:2:1.

Дата добавления: 2014-01-07