К расчету показателей центральной тенденции

Модуль1. Модульная единица 3

Занятие 2 Расчет показателей центральной тенденции и вариации в дискретном ряду распределения.

Условие. Имеются данные дискретного ряда распределения (таблица 2.1)

Требуется: Определить показатели центральной тенденции (среднюю арифметическую величину, моду, медиану).

Таблица 2.1

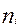
Значение признака- хi	частота-	Расчетные данные
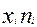
	Сумма накопленных частот Si
Итого			X

Решение.

Вначале рассчитаем среднюю арифметическую величину.

Для этого следует определить произведения индивидуальных значений признака и их частот встречаемости 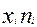а затем найдем сумму произведений и запишем ее в итоговой строке.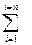

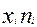
По формуле средней арифметической взвешенной определим 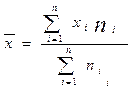=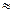4,4

Далее надо определть моду (Х_MO) в дискретном ряду

Проанализировав величину частот встречаемости, отмечаем максимальное значение- 42. Эту частоту имеет значение признака –4. Следовательно, Х_MO=4.

В заключение следует определить медиану (Х мe) в дискретном ряду

Так как медиана делит ряд на две равные части, следует установить адрес единицы, которая находится в середине ряда. В рядах распределений с нечетным числом единиц совокупности имеется конкретная единица, делящая ряд пополам. Ее адрес устанавливается по формуле n _{мe =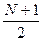} . Так как в нашей совокупности четное число единиц, то адрес медианы состоит из двух единиц. Разделим общую численность совокупности пополам (170: 2= 85). Таким образом, медианное значение признака равно половине суммы индивидуальных значений единиц с адресом n₈₅ и n₈₆

б) Для нахождения значений признака единиц с адресом n₈₅ и n₈₆ рассчитаем сумму накопленных частот и запишем в таблицу 2.1. Для расчета суммы накопленных частот (S _i) сложим последовательно частоту каждого значения признака с суммой всех предыдущих частот. Например, для значения Х=2 сумма накопленных частот равна 11+10=21, для Х = 3 -

29+21=50 и т.д. Следует помнить, что сумма накопленных частот всей совокупности S _i равна общей численности совокупности .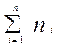

в) Определим по сумме накопленных частот, что единицы с адресами № 85 и № 86 впервые встречаются в накопленной частоте S _i =92, которая соответствует значению признака, равному 4_. Это значение и будет медианой Х _me = 4

Рассчитаем показатели вариации в дискретном ряду распределения

Для этого надо составить таблицу 2.2, при этом в колонке 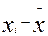от каждого значения признака следует отнять его среднее значение найденное ранее:

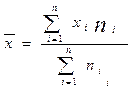= 4.4

Таблица 2.2

К расчету показателей центральной тенденции в дискретном ряду

распределения

Значение признака- хi	частота-
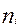
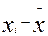
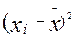
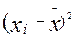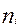
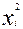
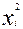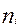
		-3,4	11,56	115,6
		-2,4	5,76	63,36
		-1,4	1,96	56,84
		-0,4	0,16	6,72
		0,6	0,36	12,60
		1,6	2,56	58,88
		2,6	6,76	135,20
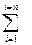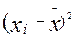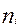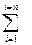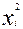Итого				= =492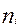.0		= =3670

Следовательно, вариация будет характеризоваться следующими показателями:

Размахом вариации R = 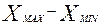= 7-1 =6

Объемом вариации W = 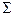(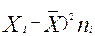= 492.0

Дисперсией =

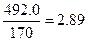
Средним квадратическим отклонением ==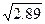1,70

Коэффициентом вариации =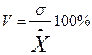

Дисперсия может быть рассчитана по иной формуле:

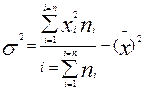=21,59-19,36=2,23

Некоторые расхождения в расчетах обусловлены округлением средней.

Выполнив расчеты показателей центральной тенденции и вариации, в заключение следует сделать выводы по полученным результатам.

Дополнительно студенты могут провести расчеты среднего из отрицательных отклонений, среднего из положительных отклонений, среднего линейного отклонения.

Дата добавления: 2014-01-07