Модуль1 . Модульная единица 3

Занятие 3 Расчет показателей центральной тенденции, вариации, ассиметрии и эксцесса в интервальном ряду распределения.

Условие: Имеются данные интервального ряда распределения (таб.3.1)

Требуется: Определить показатели центральной тенденции (среднюю арифметическую, моду и медиану).

Вначале необходимо составить макет таблицы, внося туда результаты построения интервального ряда (занятие 1) и произвеcсти необходимые расчеты таб.3.1)

Таблица 3.1

Исходные и расчетные данные для определения средней арифметической величины, моды и медианы.

№п/п	Интервалы значений признака	Частота интервала	Срединное значение интервала (варианта) (Хi)	Произведение вариант на частоту (Хi ni)	Сумма накоплен ных частот (Si)
	А
	22,0 - 26,0
	26,0 - 30,0
	30,0 - 34,0
	34,0 - 38,0
	38,0 - 42,0
	42,0 - 46,0
	46,0 - 50,0
	50,0 - 54,0
	54,0 - 58,0
	Итого		х		х

Для расчета средней арифметической взвешенной:

а) Определим срединные значения интервалов (варианты) как полусумму значений нижней и верхней границ интервалов (графа 2)

б) Найдем произведение вариант на частоту (Х_i ni) и сумму произведений (графа 3).

в) Рассчитаем среднюю арифметическую величину по формуле

Для расчета моды в интервальном ряду интерполяционным методом

а) Определим модальный интервал, то есть интервал с наибольшей частотой. Модальным является интервал 34,0 – 38,0, так как он имеет максимальную частоту - 50.

б) Вычислим приближенное модальное значение признака, для чего используем формулу = =

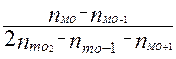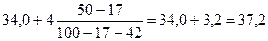
В заключение следует рассчитать медиану в интервальном ряду интерполяционным методом, для чего

а) Для каждого интервала определим накопленную частоту (таб.3.1)

б) Далее определим медианный интервал. Им является интервал 38,0-42,0, так как в нем находятся единицы, делящие ряд распределения на две равные части (170: 2=85); следовательно, в середине ранжированного ряда находятся единицы с адресами №85 и №86.

в) Рассчитаем медианное значение признака по формуле

==

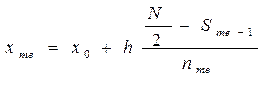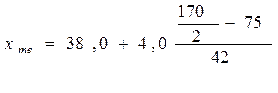38,0 + 0,9 = 38,9

Следующим этапом работы является расчет показателей вариации

Условие: имеются данные интервального ряда распределения (таб. 1.3)

Требуется: определить показатели вариации. Дисперсию вычислить по основной и рабочей формулам.

Решение.

1 Вначале определим размах вариации. R=X_max - X_min = 58,0-22.0=36.0

Вывод: В изучаемой совокупности хозяйств максимальные различия в составляют 36 единиц

3.Исчислим дисперсию по основной формуле, для чего:

а) вычислим квадраты отклонений от средней (графа 5);

б) определим взвешенные частотами квадраты отклонений и их сумму (гр. 6)

в) вычислим дисперсию

=

4. Определим дисперсию по рабочей формуле:

а) найдем квадраты значений признака (графа 7);

б) рассчитаем взвешенные частотами квадраты значений признака и их сумму (графа 9);

в) вычислим дисперсию

=

Небольшое различие в величине дисперсии, исчисленной по основной и рабочей формулам, обусловлено округлениями в расчетах.

5. Рассчитаем среднее квадратическое отклонение

=

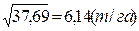
Вывод: среднее квадратическое отклонение показывает, что все варианты отклоняются от средней величины в среднем на 6, 14 (т/га)

6. Определим относительные характеристики вариации.

Коэффициент осцилляции =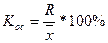

Вывод: относительная колеблемость крайних значений урожайности по хозяйствам высокая.

Относительное линейное отклонение =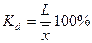

Вывод: средняя колеблемость урожайности по хозяйствам низкая и составляет 12,15 %, что свидетельствует об однородности совокупности.

6. Определим коэффициент вариации:

=

Вывод: коэффициент вариации, более точно характеризуя относительную вариацию признака, подтверждает, что мера колеблемости в данном ряду распределения невысокая (менее 33 %), и совокупность является однород-ной по изучаемому признаку.

Дата добавления: 2014-01-07