Интервальная оценка генеральной средней и доли

Модуль2. Модульные единицы 6, 7

Занятие 5 Типовые задачи выборочного метода, решаемые на основе больших выборок

. Данная задача решается в такой последовательности:

1.1) из генеральной совокупности численностью в N единиц механическим способом осуществляется выборка численностью 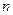единиц, при этом численность выборки должна больше тридцать единиц

1.2) по выборочной совокупности определяется выборочная средняя, как оценка для средней генеральной; при ее расчете может быть использована формула средней арифметической простой 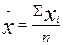или (если выборочные данные представлены вариационным рядом распределения) средней арифметической взвешенной ;

1.3) по выборочной совокупности определяется значение выборочного среднего квадратического отклонения по формулам: 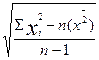(для случая простой средней) и 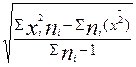(для случая, когда выборочная средняя определяется как средняя взвешенная);

1.4) определяется средняя ошибка выборочной средней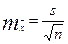

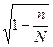
1.5) устанавливается доверительный уровень вероятности (Р);

1.6) для принятого доверительного уровня вероятности по таблицам интеграла вероятности нормального распределения находят значение коэффициента t;

1.7) определяются границы предельной ошибки ;

1.8) с принятым доверительным уровнем вероятности генеральная средняя находится в интервале

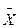0 = ±;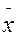

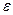1.9) для интервальной оценки генеральной доли из генеральной совокупности численностью N механическим способом формируется выборка численностью 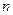единиц

1.10) по выборке определяется число единиц (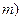с неким качеством.

1.11) находится соотношение 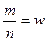- это оценка доли в генеральной совокупности;

1.12) определяется средняя ошибка для доли .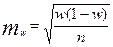

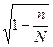
1.13) выбирается доверительный уровень вероятности- Р, по таблицам интеграла вероятностей нормального распределения находтся коэффициент t

1.14) находятся границы предельной ошибки для доли ;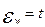

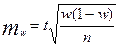
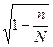1.15) определяются возможные границы доли признака в генеральной совокупности W =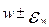

2. Определение необходимой численности выборки

Условие: величина предельной ошибки задана и составила с установленным доверительным уровнем вероятности величину ;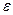

Требуется определить какова должна быть минимальная численность выборки для обеспечения заданной ошибки

Решение:

2. 1) поскольку для формирования выборки планируется использовать механический отбор, необходимую численность выборки определим по формуле:

,

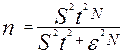при этом величину дисперсии возьмем из первой задачи, а величину коэффициента t из таблиц. По полученному результату сделаем выводы

Дата добавления: 2014-01-07