Решение. Модуль2 . Модульная единица 14

Модуль2. Модульная единица 14

Занятие 11 Проверка гипотезы относительно средних по данным двух выборок

Задача 1 Проверка гипотезы относительно двух средних по данным двух независимых выборок

Условие: имеются две малых выборки.

Требуется: на основании имеющихся выборок установить имеют ли место различия между средними по генеральным совокупностям, из которых произведены выборки

1.1) вначале следует установить характер двух выборок; если выборки независимые, то последующие шаги состоят в следующем

1.2) выдвигаем две гипотезы: Н 0: 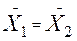, и НА: 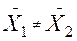(ненаправленную) или направленную НА: или наоборот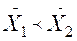

1.2) определяемся с уровнем значимости

1.3) поскольку выборки малые в качестве критерия для проверки обозначенных выше гипотез используется критерий t - Стьюдента

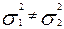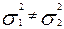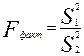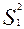1.4) определяемся с ситуацией к которой принадлежат исходные данные, для чего проверяем вспомогательную гипотезу: Н0:и соответственно НА:. Проверка этой вспомогательной гипотезы производится на основе критерия F – критерия; фактическое значение критерия рассчитывается так: , если или , если , где и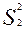 - дисперсии по выборкам; фактическое значение критерия сопоставляется с табличным, которое зависит от принятого уровня значимости и от числа степеней свободы для дисперсий по первой выборке d f (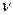)1 = n1 – 1 и по второй выборке d f (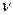)2 =п2 - 1. Принятие решение о равенстве или неравенстве дисперсий по генеральным совокупностям происходит по традиционной схеме.

1.6) в зависимости от ситуации, к которой принадлежат исходные данные, фактическое значение критерия t- Стьюдента рассчитывается по следующим алгоритмам:

При первой ситуации (равны численности выборок, равны и дисперсии) , где - среднее значение признака по первой выборке; 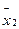- среднее значение признака по второй выборке,при этом разность между средними берется по абсолютной величине.

- усредненная дисперсия

При второй ситуации (дисперсии равны, но численности выборок не равны) фактическое значение критерия находится по формуле 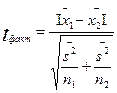, при этом формула для расчета усредненной дисперсии будет выглядеть так: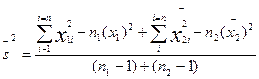

При третьей ситуации ( при равенстве численности выборок, дисперсии не равны) фактическое значение критерия определяется по формуле .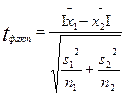

При четвертой ситуации (нет равенства в дисперсиях и в численности выборок) фактическое значение критерия определяется аналогично как и при третьей;

1.7) находим табличное значение критерия t-Стьюдента: для первых трех ситуаций, кроме уровня значимости оно зависит от числа степеней свободы, которое для первых двух ситуаций определяется по формуле: d f (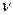) = (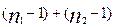. Для третьей ситуации при определении числа степеней свободы следует внести поправку и формула приобретает вид:

d f (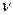) = [ (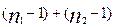] [0,5 + ]

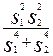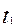Для четвертой ситуации табличное значение критерия является расчетной величиной и определяется по формуле: , где и 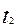- табличные значения критерия t – Стьюдента для первой и второй выборок, соответственно с числом степеней свободы и

;

1.8) Сравнивая фактическое и табличное значения критерия формулируем соответствующий вывод о выдвинутых гипотезах, при этом при направленной гипотезе для всех ситуаций табличное значение критерия берется с удвоенным уровнем значимости.

Задача 2 Проверка гипотезы относительно средних при зависимых выборках

Условие: имеются две малых выборки.

Требуется: на основании имеющихся выборок установить имеют ли место различия между средними по генеральным совокупностям, из которых произведены выборки

Дата добавления: 2014-01-07