Статистические показатели динамики

Прежде чем анализировать собственно динамику исследуемого явления или процесса, вначале оценивают его уровень в целом. Для этого рассчитывают средний уровень ряда динамики. Выбор используемой при этом формулы зависит от вида этого ряда.

Обозначим:

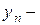, , …, все уровни последовательных периодов или моментов времени;

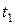, , …, длительности этих периодов;

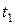, , …, интервалы между этими моментами времени.

Тогда для расчета среднего уровня используют следующие формулы:

· при равноотстоящих интервальных уровнях

;

· при неравноотстоящих интервальных уровнях

;

· при равноотстоящих моментных уровнях

;

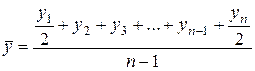· при неравноотстоящих моментных уровнях

.

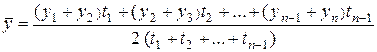Первые две формулы относятся к средней арифметической простой и средней арифметической сложной, вторые две формулы – к средней хронологической простой и средней хронологической сложной соответственно.

После определения среднего значения уровней ряда динамики проводят оценку интенсивности их изменения. Для этого рассчитывают статистические показатели динамики, используя при этом один из двух способов:

1) цепной способ расчета, когда уровни сравнивают с предшествующими;

2) базисный способ расчета, когда уровни сравнивают с одним и тем же уровнем, выбранным за базу сравнения.

Обозначим:

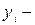текущий уровень;

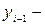предшествующий ему уровень;

базисный уровень (один из уровней, выбранный за постоянную базу сравнения).

Тогда цепные и базисные показатели динамики могут быть рассчитаны по следующим формулам:

· абсолютный прирост

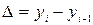или ;

· коэффициент роста

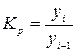или ;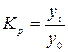

· темп роста

;

· темп прироста

;

· абсолютное значение одного процента прироста

.

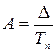Чтобы иметь полное представление о цепном или базисном изменении уровня, необходимо оценить это изменение как в абсолютном, так и в относительном выражении. Из этого следует, что показатель абсолютного прироста должен дополняться на выбор коэффициентом роста, темпом роста или темпом прироста.

Абсолютное значение одного процента прироста объединяет характеристики абсолютного и относительного изменения уровней в одном показателе. Однако его индивидуальное использование без абсолютного и относительного показателей динамики является недостаточным.

Для характеристики интенсивности развития явления за изучаемый период времени в целом рассчитывают средние показатели динамики:

· средний абсолютный прирост

;

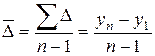· средний коэффициент роста

;

· средний темп роста

;

· средний темп прироста

;

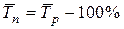· средняя величина абсолютного значения одного процента прироста

.

Применение этих формул не зависит от того, какие показатели динамики усредняются – базисные или цепные.

Рассмотрим порядок анализа статистических рядов динамики на конкретных примерах.

Пример 10.1. В таблице 10.7 представлены данные о динамике объема продаж сахарного песка торговым предприятием. Рассчитаем средний уровень ежегодного объема продаж сахарного песка в период с 2000 по 2006 гг., все цепные показатели динамики ежегодного объема продаж, их средние значения и сделаем вывод о средней динамике ежегодного объема продаж за весь период.

Таблица 10.7

Год
Объем продаж, т

Решение.

Имеет место интервальный ряд динамики с равноотстоящими уровнями, поэтому средний уровень объема продаж равен

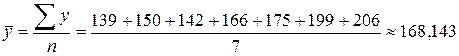т.

Абсолютные цепные приросты объёма продаж:

;

т; т; т;

т; 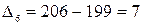т; т.

Цепные коэффициенты роста объёма продаж:

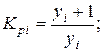
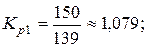
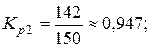
Цепные темпы роста объема продаж:

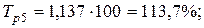
Цепные темпы прироста:

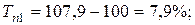
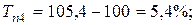
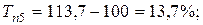
Цепные абсолютные значения одного процента прироста:

;

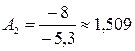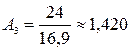т; т; т;

т; 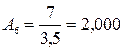т; т.

Средние значения показателей динамики:

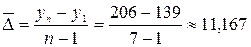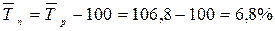т;

;

;

;

т.

Таким образом, интерпретируя рассчитанные средние показатели динамики, можно сделать следующие выводы. В период с 2000 по 2006 гг. объем продаж сахарного песка торговым предприятием ежегодно увеличивался в среднем на 11167 кг или в 1,068 раз. Следовательно, уровень продаж каждого последующего года в среднем составлял 106,8 % от уровня продаж предыдущего года, то есть был выше на 6,8 %. При этом на каждый процент этого прироста приходилось в среднем 1642 кг сахарного песка.

Пример 10.2. В таблице 10.8 представлены данные о ежеквартальной динамике стоимости основных производственных фондов промышленного предприятия (млн. руб.). Оценим динамику среднегодовой стоимости основных производственных фондов предприятия от года к году и в целом за весь рассматриваемый период времени.

Таблица 10.8

Год	Дата регистрации
01 января	01 апреля	01 июля	01 октября
	62,3	65,1	70,9	68,0
	68,5	70,1	75,3	78,4
	79,3	80,1	80,5	79,9
	81,3	-	-	-

Решение.

Имеет место моментный ряд динамики с равноотстоящими уровнями, причем первый уровень последующего года является последним уровнем предыдущего года, поэтому:

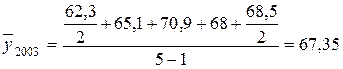млн. руб.;

Дата добавления: 2014-01-07