Млн. руб

Млн. руб.

Абсолютные, относительные и средние показатели ежегодной динамики стоимости основных производственных фондов:

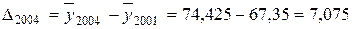млн. руб.;

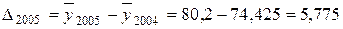млн. руб.;

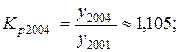
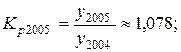
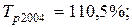
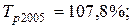
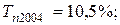
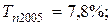
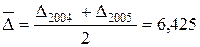млн. руб.;

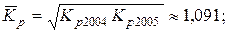
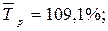
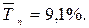
Из полученных результатов следует, что среднегодовая стоимость основных производственных фондов предприятия в 2004 г. выросла по сравнению с 2003 г. на 7,075 млн. руб. или на 10,5 %, а в 2005 г. по сравнению с 2004 г. – на 5,775 млн. руб. или 7,8 %. В среднем за весь период среднегодовая стоимость фондов ежегодно увеличивалась на 6,425 млн. руб. или на 9,1 %.

Пример 10.3. В таблице 10.9 представлены данные о динамике величины остатков двух денежных вкладов (руб.) в течение января отчетного года.

Таблица 10.9

Номер вклада	Дата регистрации данных
06 января	09 января	15 января	25 января	31 января
	+150	-	+200	+100	+50
	-	+300	+150	-200	+100

Определим разницу между значением среднего остатка по первому и по второму вкладам в течение указанного месяца, учитывая, что на начало месяца остаток по первому вкладу составил 500 руб., а по второму – 700 руб.

Решение.

Изменения остатков по первому и второму вкладам отдельно характеризуются соответствующими рядами динамики (таблицы 10.10, 10.11).

Таблица 10.10

Дата	01.01	06.01	15.01	25.01	31.01
Величина остатков по вкладу, руб.

Таблица 10.11

Дата	01.01	09.01	15.01	25.01	31.01
Величина остатков по вкладу, руб.

Оба ряда являются рядами динамики моментных величин с неравноотстоящими уровнями, поэтому средние уровни остатков по вкладам рассчитываются следующим образом:

;

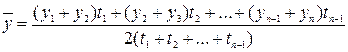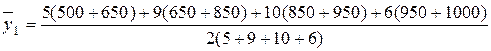
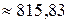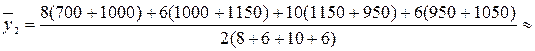
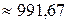руб.;

руб.

Тогда

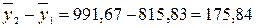руб.

Таким образом, средняя величина остатков по второму вкладу в январе отчетного года была выше этого показателя по первому вкладу на 175,84 руб.

Анализ основной тенденции ряда динамики

Изменение уровней ряда динамики в общем случае имеет три составляющие:

1) тренд – основная тенденция изменения уровней;

2) циклические колебания уровней, в том числе сезонные;

3) случайные колебания уровней.

Например, при наличии инфляции динамика розничных цен на овощи и фрукты характеризуется в целом их ростом. Это основная тенденция изменения цен. Кроме того, в зависимости от времени года цены на овощи и фрукты дополнительно возрастают или несколько снижаются относительно основной тенденции. Это свидетельствует о наличии сезонных колебаний уровней цен. Вместе с тем, из-за неритмичности поставок товара по причинам случайного характера также возможно временное изменение цен. Очевидно, что такое колебание уровней ряда динамики следует отнести к разряду случайных.

Для проверки наличия в ряду динамики основной тенденции используют разные методы. Рассмотрим порядок этой проверки на примере метода серий.

Согласно этому методу серий уровни исходного ряда динамики упорядочивают по их величине. В результате получают новый ряд значений статистического показателя – ряд распределения по величине.

Для нового ряда определяют значение его медианы. Затем возвращаются к исходному ряду и сравнивают каждый его уровень с медианой. Если уровень не превышает медиану, то ему присваивают тип А, если превышает – тип В. Значение уровней заменяют на их типы.

Следующие друг за другом одинаковые типы образуют серии. При этом минимально возможное число серий равно единице, а максимальное – числу уровней.

Если тенденции в ряду нет, то чередование типов уровней происходит случайным образом, а R является случайной величиной с нормальным законом распределения. Тогда по правилу «трех сигм» с вероятностью 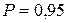число серий должно находиться в интервале

,

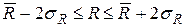где:

среднее число серий;

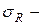среднеквадратичное отклонение числа серий.

Среднее число серий и его среднеквадратичное отклонение определяют следующим образом:

;

,

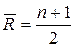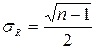где n – число уровней исследуемого ряда динамики (для получения достоверного вывода о наличии или отсутствии основной тенденции оно должно быть не менее десяти).

Поскольку число серий – это целое число, то указанные границы интервала раздвигают до целых значений. Попадание числа серий в интервал свидетельствует об отсутствии в ряду динамики какой-либо основной тенденции, а непопадание – о ее наличии.

Пример 10.4. В таблице 10.12 представлены данные о динамике ежемесячного объема реализации продукции (млн. руб.) предприятием за отчетный год. Проверим наличие в представленном ряду динамики основной тенденции, используя метод серий.

Таблица 10.12

Номер месяца
Объем реализации	15,2	14,8	14,5	16,0	15,4	15,8	16,7	16,1	17,3	16,9	17,5	18,0

Решение.

Преобразуем ряд динамики в ряд распределения:

{14,5; 14,8; 15,2; 15,4; 15,8; 16,0; 16,1; 16,7; 16,9; 17,3; 17,5; 18,0}.

Определим медиану ряда распределения:

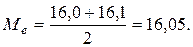
Вернемся к ряду динамики и заменим его уровни на типы:

· А, если ;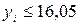

· B, если .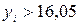

В результате получаем чередование типов уровней:

{ A; A; A; A; A; A; B; B; B; B; B; B }.

При этом число серий R = 2.

Проверим, является ли величина R случайной с нормальным законом распределения. Для этого рассчитаем среднее число серий и среднеквадратическое отклонение числа серий:

;

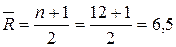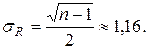
Определим границы доверительного интервала при доверительной вероятности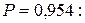

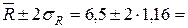3,18; 9,82.

Раздвинем полученные границы до целых величин:

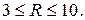
При R= 2 данное условие не выполняется. Следовательно, число серий не является случайной величиной, а в рассматриваемом ряду динамики имеется какая-то основная тенденция.

После обнаружения основной тенденции определяют ее характер. Для этого используют один из трех методов – укрупнения временных интервалов, скользящей средней или аналитического выравнивания.

· Метод укрупнения интервалов.

В этом случае исходные временные интервалы между уровнями объединяют в более крупные (например, месячные – в квартальные). Для укрупненных интервалов рассчитывают новые уровни, усредняя старые по соответствующей формуле средней. В результате колебания значений исходных уровней сглаживаются и характер основной тенденции становится более явным.

Пример 10.5. Определим характер основной тенденции, выявленной в примере 10.4, используя метод укрупнения временных интервалов (в нашем случае до кварталов).

Решение.

Рассчитаем на основе двенадцати месячных уровней четыре значения среднего месячного уровня в рамках каждого квартала. Поскольку исследуемый ряд динамики является интервальным рядом с равноотстоящими по времени уровнями, то:

;

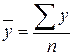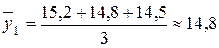млн. руб.;

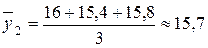млн. руб.;

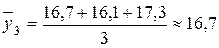млн. руб.;

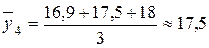млн. руб.

Рассчитаем ценные абсолютные приросты найденных средних уровней:

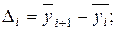
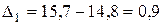млн. руб.;

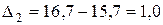млн. руб.;

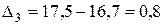млн. руб.

Поскольку наблюдаются относительно стабильные цепные приросты уровней, то это свидетельствует о линейном характере основной тенденции.

· Метод скользящей средней.

В этом случае уровни исходного ряда заменяют на средние величины. Усреднение проводят для значений рассматриваемого уровня и четного числа уровней, расположенных симметрично от него справа и слева. Для уровней, расположенных по краям ряда и не имеющих необходимое число соседей с одной из сторон, усреднение не проводится. Например, при трехуровневом усреднении первый и последний уровни исключают из рассмотрения, а для остальных используют соответствующую формулу средней и тем самым уменьшают циклическую и случайную компоненты их динамики.

Уменьшение числа уровней при использовании метода скользящей средней снижает достоверность вывода о характере основной тенденции. В этом состоит недостаток данного метода. Однако все же в этом случае число новых уровней будет гораздо больше, чем при использовании метода укрупнения интервалов.

Пример 10.6. Определим характер основной тенденции, выявленной в примере 10.4, используя метод скользящей средней с трехуровневым периодом сглаживания.

Решение.

Заменим все исходные уровни, начиная со второго и заканчивая одиннадцатым, на средние величины:

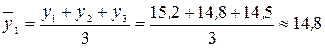млн. руб.;

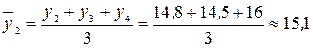млн. руб.;

млн. руб.;

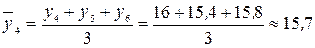млн. руб.;

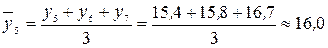млн. руб.;

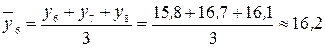млн. руб.;

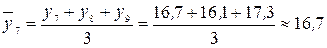млн. руб.;

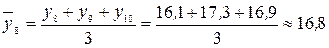млн. руб.;

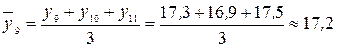млн. руб.;

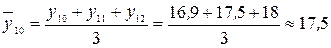млн. руб.

Рассчитаем цепные абсолютные приросты новых уровней:

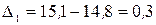млн. руб.; 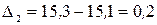млн. руб.;

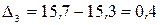млн. руб.; 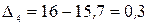млн. руб.;

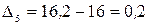млн. руб.; 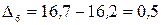млн. руб.;

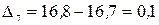млн. руб.; 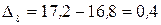млн. руб.;

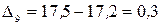млн. руб.

В целом наблюдаются стабильные абсолютные приросты уровней (стабильные относительно значений самих уровней), что также свидетельствует о наличии в исследуемом ряду динамики линейной тенденции.

· Метод аналитического выравнивания.

В этом случае уровни ряда выражают функцией времени .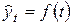

В статистике чаще всего используют три вида этой функции:

o линейную функцию

,

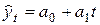когда наблюдаются стабильные цепные абсолютные приросты уровней;

o параболическую функцию

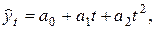
когда сами цепные приросты уровней изменяются, но величина этого изменения стабильна;

o экспоненциальную функцию

,

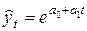когда наблюдаются стабильные цепные коэффициенты роста уровней.

Параметры этих функций определяют на основе методов регрессионного анализа. Например, для определения параметров линейного уравнения тренда необходимо применить метод наименьших квадратов и решить систему уравнений

.

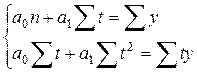Если интервалы времени между уровнями равны, то в целях упрощения решения 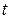присваивают такие целые значения, что 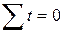. Например, {-1; 0; 1} или {–3; -1; 1; 3}. Тогда расчет искомых параметров упрощается:

; .

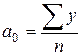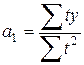При ограниченном числе уровней уравнение тренда проверяют на адекватность фактическим данным. Независимо от вида уравнения эту проверку можно осуществить на основе критерия Фишера

,

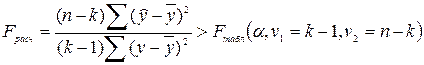где:

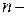число уровней анализируемого ряда динамики;

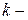число параметров уравнения тренда;

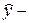теоретические значения уровней, определяемые из уравнения тренда;

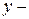фактические значения уровней;

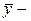средний фактический уровень;

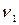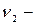, числа степеней свободы.

Если критерий выполняется, то уравнение тренда с вероятностью 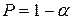признается адекватным фактической основной тенденции исследуемого ряда динамики.

Пример 10.7. Определим аналитическое выражение линейной основной тенденции, выявленной в примерах 10.5, 10.6, и оценим его адекватность.

Решение.

Искомое уравнение имеет вид

.

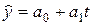Заменим фактические номера месяцев t на условные, такие что :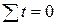

t= -11; -9; -7; -5; -3; -1; 1; 3; 5; 7; 9; 11.

Тогда:

; .

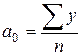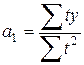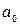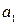Для определения параметров и заполним графы 1 – 5 таблицы 10.13.

Таблица 10.13

№ п/п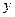
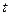
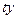
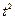
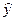
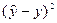
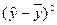
1	2	3	4	5	6	7	8
	15,2	-11	-167,2		14,621	0,335	0,966
	14,8	-9	-133,2		14,905	0,011	1,913
	14,5	-7	-101,5		15,189	0,475	2,832
	16,0	-5	-80,0		15,473	0,278	0,033
	15,4	-3	-46,2		15,757	0,127	0,613
	15,8	-1	-15,8		16,041	0,058	0,147
	16,7		16,7		16,325	0,141	0,267
	16,1		48,3		16,609	0,259	0,007
	17,3		86,5		16,893	0,166	1,248
	16,9		118,3		17,177	0,077	0,514
	17,5		157,5		17,461	0,002	1,734
	18,0		198,0		17,475	0,065	3,301
Итого	94,2		81,4		-	1,994	13,575

В результате:

; ;

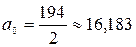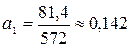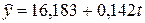при .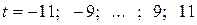

Необходимо отметить, что найденное уравнение соответствует условным значениям 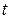. Чтобы вернуться от условных к реальным значениям времени (порядковым номерам месяца), в уравнение вместо параметра t необходимо подставить выражение 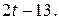Тогда уравнение тренда примет вид

,

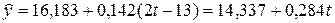соответствующий значениям .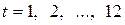

Проверим адекватность найденного уравнения фактическим данным. Для определения расчетного значения критерия Фишера подставим значения t в уравнение тренда (условные в первый вариант уравнения или реальные во второй вариант) и заполним графы 6 -7 таблицы 10.13.

В результате:

.

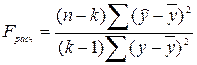
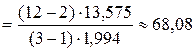Выбираем 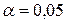, тогда

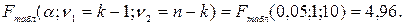
Поскольку 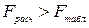, то с вероятностью 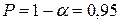можно утверждать, что найденное уравнение тренда адекватно фактической основной тенденции.

Зная характер основной тенденции ряда динамики, можно прогнозировать изменение его уровней во времени. Различают два вида прогнозирования – экстраполирование и интерполирование. Экстраполирование – это прогнозирование уровней за пределами ряда динамики, интерполирование – внутри (между зарегистрированными значениями уровней). Оба вида прогнозирования основаны на применении одного из трех методов прогнозирования – по среднему абсолютному приросту, по среднему коэффициенту роста и по уравнению тренда.

· Метод прогнозирования уровней по среднему абсолютному приросту.

Данный метод применяют при наличии линейной основной тенденции, делая прогноз по формуле

,

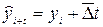где:

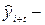значение прогнозируемого уровня;

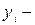фактическое значение 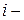го уровня;

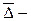средний абсолютный прирост уровней;

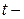срок прогноза.

Пример 10.8. В таблице 10.14 представлены данные о динамике объема грузооборота транспортного предприятия (тыс. т). Спрогнозируем объем грузооборота предприятия в 2007 году.

Таблица 10.14

Год
Грузооборот

Решение.

Проверим наличие линейного характера в изменении уровней грузооборота. Для этого рассчитаем значения цепного абсолютного прироста уровня годового грузооборота:

;

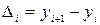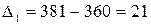тыс. т; 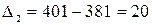тыс. т;

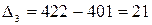тыс. т; 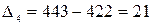тыс. т;

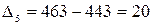тыс. т; 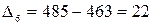тыс. т.

Абсолютные приросты уровней стабильны, что свидетельствует о наличии в ряду линейной основной тенденции. В этом случае для прогнозирования уровней можно применить среднее значение абсолютного прироста

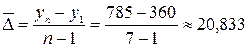тыс. т.

За начало отсчета срока прогноза выберем 2006 год. Тогда прогнозируемый уровень грузооборота в 2007 году составит

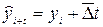
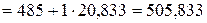тыс. т.

· Метод прогнозирования уровней по среднему коэффициенту роста.

Метод применяют при экспоненциальной тенденции, используя для прогноза формулу

,

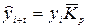где 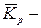средний коэффициент роста уровней.

Пример 10.9. В таблице 10.15 представлены данные о динамике объема оплаченных поездок (тыс. км), выполненных таксомоторным парком. Спрогнозируем суммарный объем оплаченных поездок таксомоторного парка на период 2007 – 2009 гг.

Таблица 10.15

Год
Объем поездок

Решение.

Определим характер изменения уровней ежегодного оплаченных поездок. Для этого вначале рассчитаем ценные абсолютные приросты этих уровней:

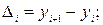
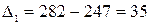тыс. т; 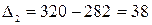тыс. т;

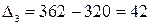тыс. т; 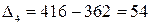тыс. т;

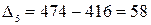тыс. т; 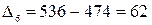тыс. т.

Абсолютные приросты уровней не стабильны, что свидетельствует об отсутствии линейного характера в их изменении.

Рассчитаем ценные коэффициенты роста уровней:

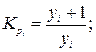
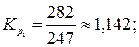
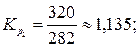
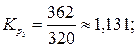
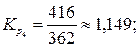
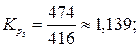
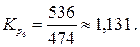
Наблюдаются относительно стабильные коэффициенты роста уровней. Следовательно, имеет место основная тенденция изменения уровней экспоненциального характера. В этом случае прогноз уровней следует делать на основе среднего значения коэффициента роста

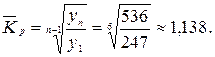
За точку отсчета при прогнозировании возьмем 2006 год. Тогда:

;

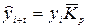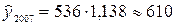тыс. км;

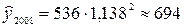тыс. км;

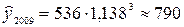тыс. км;

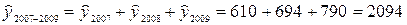тыс. км.

Таким образом, прогнозируемый суммарный объем оплаченных поездок таксомоторного парка за период 2007 – 2009 гг. составляет 2094 тыс. км.

· Метод прогнозирования уровней по уравнению тренда.

Данный метод может применяться при любой форме основной тенденции и основан на использовании соответствующего уравнения тренда, адекватного этой тенденции. В уравнение подставляют значение переменной, соответствующее сроку прогноза, и таким образом получают точечное значение прогнозируемого уровня. Это значение рассматривается как наиболее вероятная фактическая величина прогнозируемого уровня. Следовательно, точечный прогноз обладает определенной погрешностью. Причина этого заключается в погрешности, с которой найденное уравнение тренда описывает фактическую тенденцию. В качестве характеристики этой погрешности используют показатель среднеквадратичной ошибки тренда

.

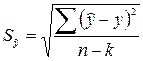Исходя из нормального закона распределения значения прогнозируемого уровня как случайной величины, с вероятностью 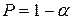гарантируют, что его фактическое значение попадет в интервал

,

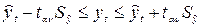где 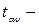коэффициент доверия, определяемый по таблице распределения Стьюдента для выбранного уровня значимости 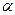и числа степеней свободы .

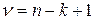Таким образом, данный метод позволяет сделать интервальный прогноз изменения уровней ряда динамики, гарантируя его с определенной вероятностью.

Пример 10.10. Вернемся к исходным данным и результатам, полученным в примере 10.8, сделаем интервальный прогноз грузооборота предприятия в 2007 году на основе уравнения тренда и оценим достоверность этого прогноза.

Решение.

Искомое уравнение тренда имеет вид

.

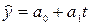Присвоим параметру t условные значения, при которых :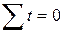

.

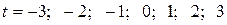Тогда:

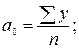
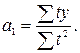
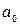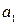Для определения и заполним графы 1 – 5 таблицы 10.16.

Таблица 10.16

Год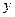
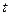
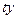
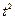
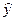
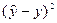
1	2	3	4	5	6	7
			-1080		359,89	0,0121
		-2	-762		380,64	0,1296
		-1	-401		401,39	0,1524
					422,14	0,0196
					442,89	0,0121
					463,64	0,4096
					484,39	0,3721
Итого					-	1,1072

Тогда:

; ;

.

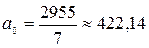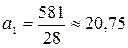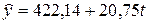Для 2007 года срок прогноза 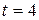. Тогда прогнозируемый уровень грузооборота за этот год равен

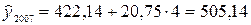тыс. т.

Заполним графы 6, 7 таблицы 10.16 и определим границы доверительного интервала для полученного точечного прогноза:

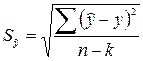
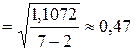тыс. т.

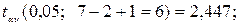
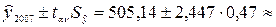504,00; 506,29 тыс. т.

Таким образом, прогнозируемый в 2007 году уровень грузооборота предприятия с вероятностью 0,95 находится в пределах от 504 до 506,29 тыс. т.

Дата добавления: 2014-01-07