
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бесконечно удаленная точка
|
|
|
|
.
.
Итак.
 . (3)
. (3)
4. n = -2, -3, -4, …. Выкладки в этом случае такие же, как и в предыдущем.
 (4)
(4)
вследствие периодичности первообразной.
Итак, мы доказали, что  при целом n не равен нулю в единственном случае - когда n = -1 и точка z 0 лежит в области, ограниченной контуром. В этом случае
при целом n не равен нулю в единственном случае - когда n = -1 и точка z 0 лежит в области, ограниченной контуром. В этом случае
Замечание. Строго говоря, перебирая различные возможности, мы не рассмотрели вариант, когда точка z 0 лежит на контуре L. В этом случае подынтегральная функция теряет определенность в точке z 0, и необходима теория несобственных комплексных интегралов. В то же время очевидно, что если точка z 0 → L, находясь внутри контура L, то  , если же z извне контура L, то
, если же z извне контура L, то 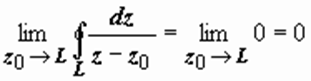 . Вообще эти вопросы - предмет теории Сохоцкого.
. Вообще эти вопросы - предмет теории Сохоцкого.
Интегральная формула Коши.
Теорема. Пусть w = f (z) аналитична в области D и L - замкнутая кусочно-гладкая кривая, содержащаяся в D вместе с областью D 1, которую она ограничивает. Тогда для каждой точки z 0 ∈ D 1 имеет место формула
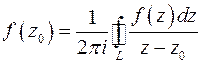 . (5)
. (5)
 Доказательство. Заметим, что в этой формуле функция в точке z 0 «портится» как раз введением множителя
Доказательство. Заметим, что в этой формуле функция в точке z 0 «портится» как раз введением множителя 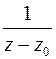 . Доказательство очень похоже на доказательство того, что
. Доказательство очень похоже на доказательство того, что  . Мы окружим точку z 0 окружностью L ρ радиуса ρ столь малого, что на L ρ функция f (z) мало отличается от f (z 0): f (z) ≈
. Мы окружим точку z 0 окружностью L ρ радиуса ρ столь малого, что на L ρ функция f (z) мало отличается от f (z 0): f (z) ≈ 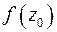 , тогда
, тогда
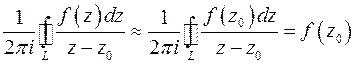 . (6)
. (6)
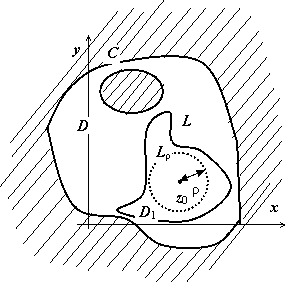
Более строго, возьмём ρ столь малым, что окружность L ρ радиуса ρ с центром в z 0 лежит в D 1. Функция w = f (z) аналитична в двусвязной области, заключенной между L и L ρ, поэтому (следствие Теоремы Коши для многосвязной области)

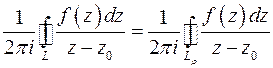 .
.
Распишем последний интеграл: 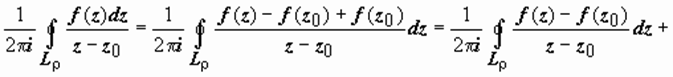
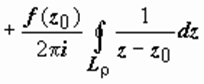 . Второй интеграл здесь равен
. Второй интеграл здесь равен 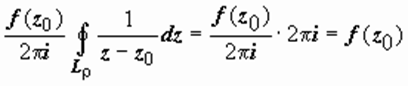 . Первый интеграл а). не зависит от ρ (действительно, подынтегральная функция аналитична в области между L ρ и L ρ1, где L ρ1 - окружность радиуса ρ1 < ρ, и по тому же следствию из Теоремы Коши для многосвязной области
. Первый интеграл а). не зависит от ρ (действительно, подынтегральная функция аналитична в области между L ρ и L ρ1, где L ρ1 - окружность радиуса ρ1 < ρ, и по тому же следствию из Теоремы Коши для многосвязной области  ; б).
; б).
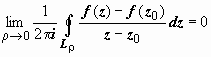 .
.
Из утверждений а) и б) следует, что первый интеграл 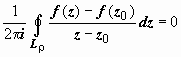 .
.
Докажем утверждение б). Обозначим M ρ = max | f (z) − f (z 0)| при z ∈ L ρ, при этом, вследствие непрерывности функции, M ρ → 0 при ρ → 0. Оценим

по модулю (учитывая, что z − z 0 = ρ e i φ, z = z 0 + ρ e i φ, dz = i ρ e i φ d φ) 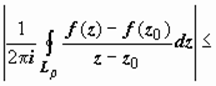
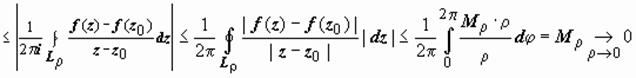 . Утверждение доказано. Доказана и интегральная формула Коши:
. Утверждение доказано. Доказана и интегральная формула Коши: 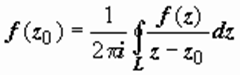 .
.
Сформулируем несколько следствий из доказанной теоремы.
1. Значения аналитической в некоторой области функции полностью определяются её значениями на границе этой области. Этот факт можно сформулировать в виде теоремы о среднем. Возьмём ρ такое, что окружность L ρ радиуса ρ с центром в z 0 лежит в D 1. Тогда z − z 0 = ρ e i φ, z = z 0 + ρ e i φ, dz = i ρ e i φ d φ,
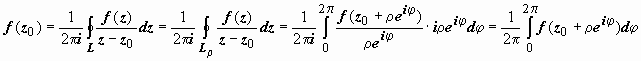 . Поэтому справедлива
. Поэтому справедлива
2. Теорема о среднем. Значение аналитической функции в каждой точке z 0 равно среднему арифметическому её значений на любой окружности с центром в точке z 0.
Теорема доказана в предположении, что точка z 0 лежит внутри контура L. Если z 0 находится вне контура, то 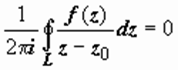 , так как подынтегральная функция аналитична в
, так как подынтегральная функция аналитична в 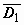 .
. 
3. Формула справедлива и для многосвязной области, если под кривой L подразумевать полную границу области. В дальнейшем нам понадобится такой вариант: f (z) аналитична в замкнутом кольце, ограниченном окружностями LR и L ρ. Тогда для всех z, лежащих внутри кольца,
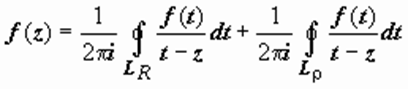 (7)
(7)
при этом окружности проходятся так, что область остаётся слева. В последней формуле переобозначены переменные: z 0 → z, z → t.
Бесконечная дифференцируемость аналитической функции. Запишем интегральную формулу Коши в переменных z, 

Продифференцируем эту формулу по z:
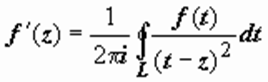
(на самом деле законность дифференцирования интеграла по параметру z требует обоснования; мы примем этот факт без доказательства).
Продолжим дифференцирование:
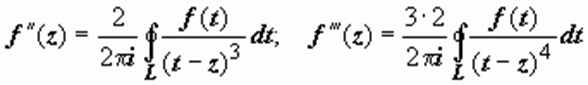
; 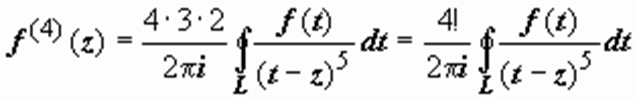 ,
,
и вообще
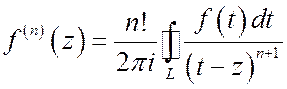 . (8)
. (8)
Следовательно:
Если функция f (z) имеет в каждой точке области D производную первого порядка (т.е. аналитична в области D), то она имеет в этой области производную любого порядка (т.е. любая производная функции f (z) аналитична в области D). Это свойство существенно отличает аналитические ФКП от дифференцируемых функций действительной переменной.
Применение интегральных формул Коши к вычислению интегралов.
Запишем формулы Коши в виде
 ,
,
 .
.
С помощью этих формул вычисляются интегралы от функций вида 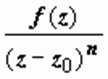 , где f (z) - аналитическая функция. Естественно, точка z 0 должна лежать внутри контура L (если она лежит вне контура, подынтегральная функция аналитична, и интеграл равен нулю).
, где f (z) - аналитическая функция. Естественно, точка z 0 должна лежать внутри контура L (если она лежит вне контура, подынтегральная функция аналитична, и интеграл равен нулю).
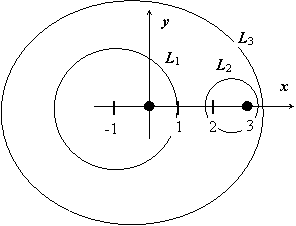
Примеры: 1. 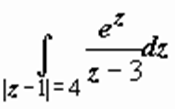 .
.
Здесь f (z) = ez, z 0 = 3 лежит внутри круга | z - 1| = 4, поэтому  .
.
2.  .
.
Здесь внутри круга L 1 = { z: | z + 1| = 2} лежит точка z 0 = 0, поэтому f (z) = sin z / (z – 3) и  .
.
3.  .
.
Здесь внутри круга L 2 = { z: | z - 2,5| = 1} лежит точка z 0 = 3, поэтому f (z) = sin z / z и 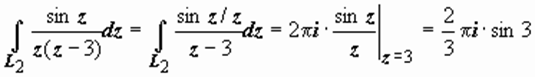 .
.
4.  .
.
Здесь внутри круга L 3 = { z | | z | = 4} лежат обе точки z 0 = 0 и z 01 = 3, но, по следствию из Теоремы Коши для многосвязной области,
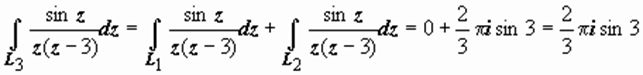 .
.
5. 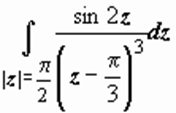 .
.
Для вычисления этого интеграла воспользуемся формулой 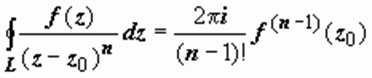 при
при 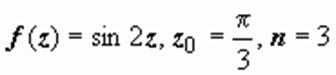 :
: 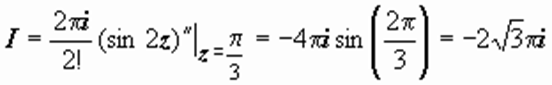 .
.
.
 Ряды Тейлора.
Ряды Тейлора.
Пусть функция w = f (z) аналитична в области D, z 0∈ D. Обозначим L окружность с центром в z 0, принадлежащую области D вместе с ограниченным ею кругом. Тогда для любой точки z, лежащей внутри L,  . Представим множитель
. Представим множитель 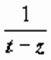 в виде суммы сходящейся геометрической прогрессии:
в виде суммы сходящейся геометрической прогрессии: 
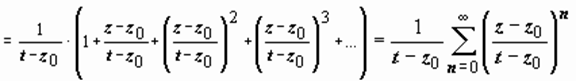 ,(так как | z – z 0| < | t – z 0|, то
,(так как | z – z 0| < | t – z 0|, то  ) и ряд сходится абсолютно, поэтому его можно почленно интегрировать:
) и ряд сходится абсолютно, поэтому его можно почленно интегрировать: 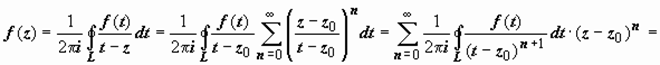
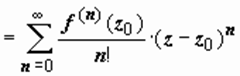 , (1)
, (1)
так как
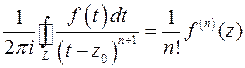 .
.
Итак,
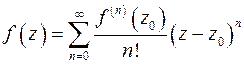 . (2)
. (2)
.
Ряд в правой части этого равенства - ряд Тейлора функции f (z). Этот ряд абсолютно сходится внутри контура L, а в качестве L можно взять любую окружность, которая не выходит за пределы области D. Доказана
Теорема о разложении функции в ряд Тейлора. Если функция w = f (z) аналитична в области D, z 0 ∈ D, то функция f (z) может быть разложена в ряд Тейлора по степеням (z – z 0) n. Этот ряд абсолютно сходится к f (z) внутри круга | z – z 0| < r, где r - расстояние от z 0 до границы области D (до ближайшей к z 0 точки, в которой функция теряет аналитичность). Это разложение единственно.
Единственность разложения следует из того, что коэффициенты ряда однозначно выражаются через производные функции.
Стандартные разложения. Для однозначных функций разложения в ряд Тейлора в принципе не могут отличиться от изучавшихся ранее разложений:
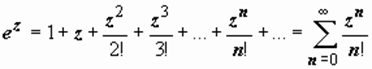 ; (3)
; (3)
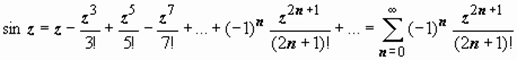 ; (4)
; (4)
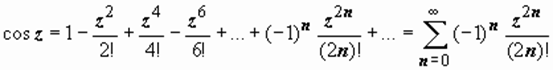 ; (5)
; (5)
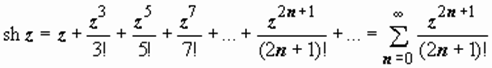 ; (6)
; (6)
 . (7)
. (7)
Все эти ряды сходятся к своим функциям на всей плоскости (при ∀ z ∈ C). Для геометрических прогрессий имеют место формулы
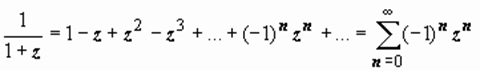 ; (8)
; (8)
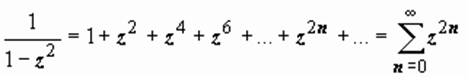 . (9)
. (9)
То, что эти ряды сходятся при | z | < 1, понятно. Ближайшие к центру разложения z 0 = 0 точки, в которых функции теряют аналитичность (граница области D) - это точки z = ±1, в которых соответствующие функции неопределены. Также имеем
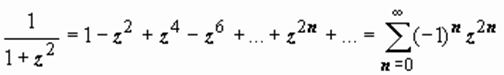 . (10)
. (10)
В действительном случае вообще было непонятно, почему этот ряд перестаёт сходиться к f (x) при | x | ≥ 1, ведь f (x) определена на всей действительной прямой. В комплексном случае это проясняется - на окружности | z | = 1 расположены точки z = ± i, в которых f (z) не определена.
При разложении многозначных функций необходимо выделить однозначную ветвь. Обычно задают значение функции в одной точке. Рассмотрим, например, разложение функции ln(z + 1). Ln 1 = ln 1 + i arg 1 = 2 k π i, k - целое. Возьмём ту ветвь логарифма, для которой Ln 1 = 0 (k = 0), т.е. главное значение логарифма
f (z) = ln (z + 1). На этой ветви
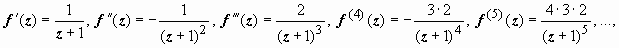
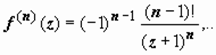 , поэтому
, поэтому 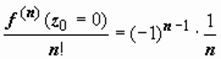 , и
, и
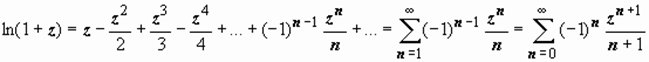 . (11)
. (11)
Точка, в которой функция теряет аналитичность (она в этой точке вообще не определена) - это z = -1, поэтому ряд сходится при | z | < 1.
Теперь рассмотрим биномиальный ряд для функции f (z) = (1 + z) α. Это (при любом комплексном α) общая степенная функция, поэтому f (z) = (1 + z) α = z α ln(1 + z ) (однозначная ветвь выделена тем, что взято главное значение логарифма); дальше находим производные: 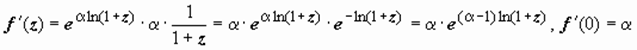 ; аналогично
; аналогично 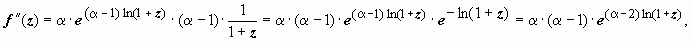 f ″(0) = α (α − 1); и т.д.; f ( n )(0) = α (α − 1)…(α − n + 1), поэтому
f ″(0) = α (α − 1); и т.д.; f ( n )(0) = α (α − 1)…(α − n + 1), поэтому
 . (12)
. (12)
Решение задач на разложение функций в ряд. Техника решения этих задач ничем не отличается от действительного случая. Рассмотрим, например, задачу: разложить функцию 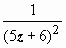 по степеням z - 7. Так как степень знаменателя равна двум, сначала разложим в ряд функцию
по степеням z - 7. Так как степень знаменателя равна двум, сначала разложим в ряд функцию 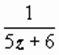 , затем почленно продифференцируем его:
, затем почленно продифференцируем его: 
. Круг сходимости  . На границе круга сходимости ряд из модулей расходится, и общий член не стремится к нулю, поэтому в каждой точке окружности
. На границе круга сходимости ряд из модулей расходится, и общий член не стремится к нулю, поэтому в каждой точке окружности 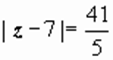 ряд расходится. Далее,
ряд расходится. Далее,
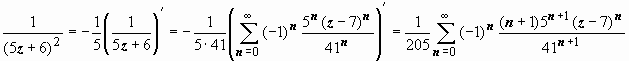
. Все выводы о круге сходимости и поведении ряда на его границе остаются справедливыми.
Пусть дана последовательность 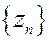 :
: 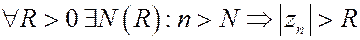 .
.
Такую последовательность назовем неограниченно возрастающей. Она предела не имеет. Вводят комплексное число 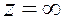 и считают всякую неограниченно возрастающую последовательность сходящейся к этому числу, которому поставим в соответствие бесконечно удаленную точку комплексной плоскости. Полная комплексная плоскость-обычная комплексная плоскость плюс
и считают всякую неограниченно возрастающую последовательность сходящейся к этому числу, которому поставим в соответствие бесконечно удаленную точку комплексной плоскости. Полная комплексная плоскость-обычная комплексная плоскость плюс 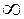 . Точки рассматриваемой последовательности с возрастанием их номера располагаются вне концентрических кругов с центром в начале координат, радиусы которых могут быть сколь угодно большими. Точки данной последовательности стремятся к точке
. Точки рассматриваемой последовательности с возрастанием их номера располагаются вне концентрических кругов с центром в начале координат, радиусы которых могут быть сколь угодно большими. Точки данной последовательности стремятся к точке 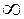 независимо от направления на полной комплексной плоскости. Из элементов неограниченно возрастающей последовательности
независимо от направления на полной комплексной плоскости. Из элементов неограниченно возрастающей последовательности 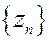 составим последовательность
составим последовательность  . Эта последовательность сходится к точке
. Эта последовательность сходится к точке  . В этой связи полагают
. В этой связи полагают 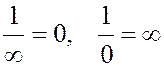 . Устанавливаются следующие соотношения
. Устанавливаются следующие соотношения
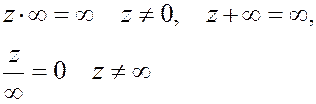 , которые естественны с точки зрения предельного перехода в операциях сложения и умножения.
, которые естественны с точки зрения предельного перехода в операциях сложения и умножения.
Ряды Лорана.
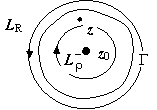
Пусть функция f (z) аналитична в кольце ρ ≤ | z − z 0| ≤ R. Тогда для любой точки этого кольца 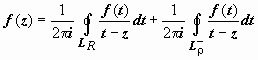 ; при этом окружности проходятся так, что область остаётся слева. Изменим в интеграле по внутренней окружности направление обхода на противоположное:
; при этом окружности проходятся так, что область остаётся слева. Изменим в интеграле по внутренней окружности направление обхода на противоположное:  . Интеграл по внешней окружности преобразуем так, как и при выводе формулы Тейлора:
. Интеграл по внешней окружности преобразуем так, как и при выводе формулы Тейлора:
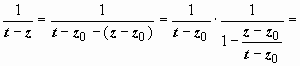
(так как | z – z 0| < | t – z 0|, то 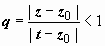 )
) 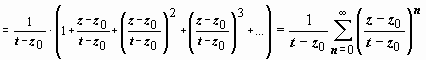 , (1)
, (1)
и ряд сходится абсолютно, поэтому его можно почленно интегрировать: 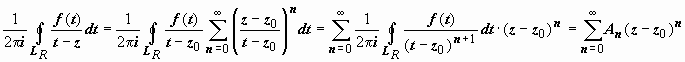 , (2)
, (2)
где
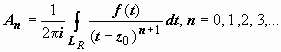 .
.
Интеграл по внутренней окружности преобразуем аналогично, учитывая только,
что на L ρ | t – z 0| < | z – z 0|:

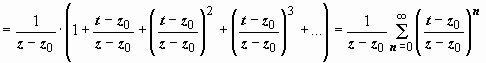 . (3)
. (3)
И здесь ряд сходится абсолютно, поэтому его можно почленно интегрировать: 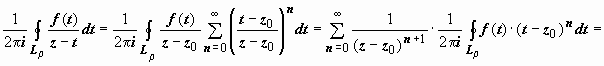
 , (4)
, (4)
 где
где
 . (5)
. (5)
Переобозначим n → − n, тогда форма коэффициентов ряда для L ρ совпадёт с формой коэффициентов ряда для LR: 
поэтому окончательно для интеграла по L ρ получим 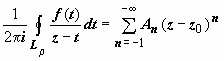 . (6)
. (6)
Докажем, что и контур для вычисления коэффициентов может быть взят один и тот же. Действительно, пусть Γ - кусочно-гладкий контур, расположенный в кольце ρ ≤ | z − z 0| ≤ R, и точка z 0 расположена внутри этого контура. По теореме Коши для многосвязной области 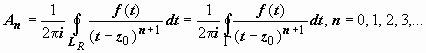 ;
; 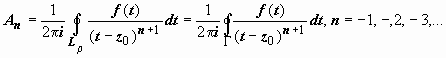 ,
,
поэтому для любого n
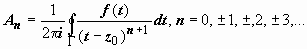 ,
,
и
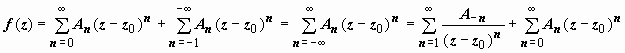 .
.
Этот ряд (содержащий и положительные, и отрицательные степени (z – z 0), называется рядом Лорана функции f (z). Его часть, содержащая неотрицательные степени
(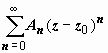 ),
),
называется правильной; часть, содержащая отрицательные степени
(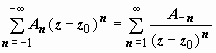 ),
),
называется главной. Правильная часть, по самому своему построению, сходится в круге | z – z 0| ≤ R, главная - во внешности круга | z – z 0| ≥ ρ, поэтому весь ряд сходится в пересечении этих областей, т.е. в кольце ρ ≤ | z – z 0| ≤ R. Так же, как и для ряда Тейлора, разложение в ряд Лорана единственно.
Еще раз подчеркнем, что в ряд Лорана раскладывается функция, аналитическая в кольце, и ширина этого кольца определяется областью аналитичности функции, т.е. разложение теряет смысл там, где функция теряет аналитичность. Рассмотрим
Примеры разложения функций в ряд Лорана. 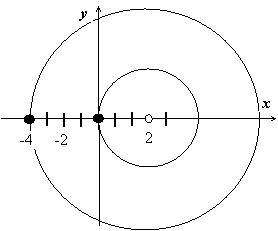
Пример 1. Требуется получить все возможные разложения в ряд Лорана по степеням z – 2 функции  .
.
Здесь z 0 = 2; функция теряет аналитичность в точках z 1 = 0, z 2 = -4. Легко видеть, что существует три области аналитичности с центром в z 0 (один круг и два кольца), на границах которых функция теряет аналитичность:
1. | z – 2| < 2; 2. 2 < | z – 2| < 6; 3. | z – 2| > 6. В каждой из этих областей разложение будет таким:
1. В первой области (круге) функция аналитична, поэтому ряд Лорана будет совпадать с рядом Тейлора. 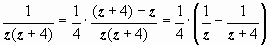 - таково разложение f (z) на простые дроби, разлагаем в ряд Тейлора каждую их них.
- таково разложение f (z) на простые дроби, разлагаем в ряд Тейлора каждую их них. 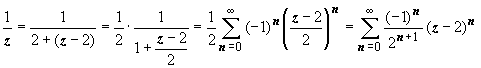 , где | z – 2| < 2;
, где | z – 2| < 2;  ; это разложение справедливо, если | z – 2| < 6, т.е. в первой и второй областях. Окончательно в первой области
; это разложение справедливо, если | z – 2| < 6, т.е. в первой и второй областях. Окончательно в первой области 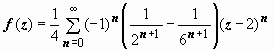 .
.
Этот ряд содержит только правильную часть.
2. В кольце 2 < | z – 2| < 6 знаменатель второй геометрической прогрессии (для дроби 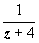 ) по модулю
) по модулю  , поэтому разложение остаётся в силе. Для первой дроби, с учётом того, что
, поэтому разложение остаётся в силе. Для первой дроби, с учётом того, что 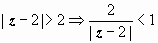 , получим
, получим 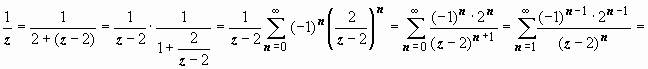 =
=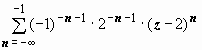 . Это - главная часть ряда Лорана. Разложение имеет вид
. Это - главная часть ряда Лорана. Разложение имеет вид 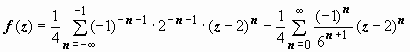 .
.
3. В кольце | z − 2| > 6 ⇔ 6 < | z − 2| < +∞ для первой дроби разложение такое же, как и в предыдущем случае: 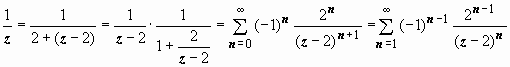
или 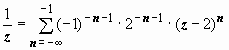 .
.
Для второй дроби 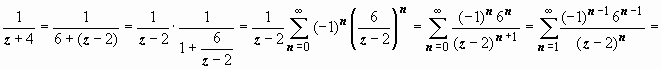
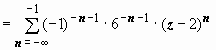 .
.
Ответ можно записать и в форме
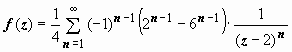 ,
,
и в форме 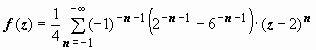 . В этом разложении имеется только главная часть.
. В этом разложении имеется только главная часть.
Пример 2. Разложить функцию 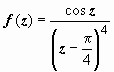 в ряд Лорана по степеням
в ряд Лорана по степеням  .
.
Решение. Здесь функция теряет аналитичность только в точке 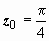 , поэтому
, поэтому 
 .
.
Главная часть здесь равна  ,
,
остальные слагаемые образуют правильную часть.
Пример 3. Разложить функцию 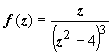 в ряд Лорана по степеням z + 2.
в ряд Лорана по степеням z + 2.
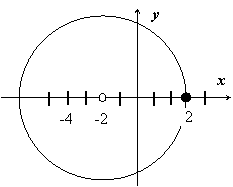 Решение. Здесь z 0 = -2; функция теряет аналитичность только в точке z 0 и в точке z 1 = 2, отстоящей от z 0 на расстоянии 4, поэтому имеется два кольца: 1. 0 < | z + 2| < 4 и 2. | z – 2| > 4.
Решение. Здесь z 0 = -2; функция теряет аналитичность только в точке z 0 и в точке z 1 = 2, отстоящей от z 0 на расстоянии 4, поэтому имеется два кольца: 1. 0 < | z + 2| < 4 и 2. | z – 2| > 4.
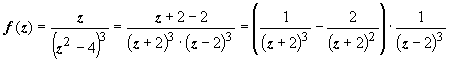 .
.
Первый множитель представлен в виде суммы по степеням | z + 2|, работаем со вторым. Третью степень в знаменателе получим, дважды дифференцируя разложение функции 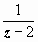 .
.
1. В первом кольце 0 < | z + 2| < 4.
Получаем
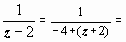
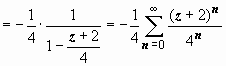 ,
, 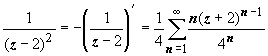 ,
, 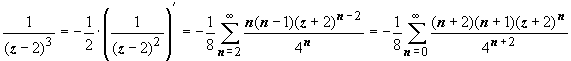 ,
, 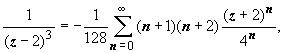
 .
.
Это и есть искомое разложение в первом кольце. Его можно преобразовывать, например, собрать вместе члены с одинаковыми степенями z + 2, выделить главную часть:  и т.д., но это уже не принципиально.
и т.д., но это уже не принципиально.
2. Во втором кольце | z + 2| > 4 получаем
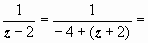
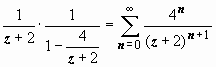 ,
, 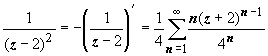
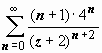 ,
, 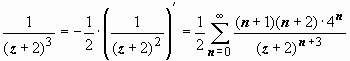 ,
, 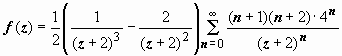 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 662; Нарушение авторских прав?; Мы поможем в написании вашей работы!