Функции. Вычеты

ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ АНАЛИТИЧЕСКОЙ

Нули аналитической функции.
Определение. Точка а называется нулём порядка k аналитической функции f (z), если f (a) = f ′(a) = f ″(a) =... = f ^{( k −1)}(a) = 0, но f ^{( k )}(a) ≠ 0.
Пример. Пусть . Точка a = 0 - нуль этой функции, так как f (0) = 0. Найдём порядок нуля: f ″(z) = − sin z + z, f ″(0)= 0, f ⁽³⁾(z) = − cos z + 1, f ⁽³⁾(0) = 0, f ⁽⁴⁾(z) = sin z, f ⁽⁴⁾(0) = 0, f ⁽⁵⁾(z) = cos z, f ⁽⁵⁾(0) = 1 ≠ 0,. Первая отличная от нуля производная функции в точке a = 0 - пятая, поэтому эта точка - нуль пятого порядка функции .
Теорема. Для того, чтобы аналитическая в точке а функция f (z) имела в этой точке нуль k -го порядка, необходимо и достаточно, чтобы в окрестности этой точки функция f (z) представлялась в виде f (z) = (z − a) ^k · φ (z), где φ (z) - аналитическая в точке а функция, и φ (a) ≠ 0.
Доказательство. Необходимость. Пусть точка а - нуль k -го порядка функции f (z), т.е. f (a) = f ′(a) = f ″(a) =... = f ^{( k −1)}(a) = 0, и f ^{( k )}(a) ≠ 0. Тогда её разложение в ряд Тейлора имеет вид , где - аналитическая (как сумма степенного ряда с тем же кругом сходимости, что и у ряда для f (z)) функция, .
Достаточность. Пусть f (z) = (z − a) ^k · φ (z), где φ (z) - аналитическая в точке а функция, и φ (a) ≠ 0. Находим производные этой функции по формуле Лейбница (uv) ^{( n )} = u ^{( n )} v + nu ^{( n - 1)} v ′ + C_n ² u ^{( n - 2)} v ″ + C_n ³ u ^{( n - 3)} v ⁽³⁾ + … + C_n ² u ″ v ^{( n - 2)} + n u ′ v ^{( n - 1)} + uv ^{( n )}: f ′(z) = k (z − a) ^{k - 1} φ (z) + (z − a) ^k φ ′(z), f ′(a) = 0; f ″(z) = k (k − 1)(z − a)^{( k - 2)} φ (z) + 2 k (z − a)^{( k - 1)} φ ′(z) + (z − a)^{( k )} φ ″(z), f ″(a) = 0;
…………… ………………………….;
f ^{( k -1)}(z) = k ·(k -1)·…2·(z − a) φ (z) + C ¹ _{k -1} k ·(k -1)·…3·(z − a)² φ ′(z) + … + (z − a) ^k φ ^{(k -1)}(z), f ^{(k -1)}(a) = 0;
f ^(k)(z) = k ·(k -1)·…2·1· φ (z) + C ¹ _k k ·(k -1)·…2·(z − a) φ ′(z) + … + (z − a) ^k φ ^{( k )}(z), f ^{( k )}(a) = k!· φ (a) ≠ 0, что и требовалось доказать.
Из этой теоремы следует, что если многочлен

P _n (z) = a ₀ z ⁿ + a ₁ z ^{n - 1} + a ₂ z ^{n - 2} + … + a _{n - 1} z = 0 (1)

разложен на множители

P _n (z) = a ₀ (z − z ₁) ^k ₁ (z − z ₂) ^k ₂ … (z − z_l) ^k_l, (2)

то корни z ₁, z ₂, …, z_l являются нулями функции P _n (z) кратностей, соответственно, k ₁, k ₂, …, k_l.

Изолированные особые точки.

Определение. Точка а называется изолированной особой точкой функции f (z), если существует окрестность этой точки, в которой f (z) аналитична во всех точках, за исключением точки а.
Рассмотрим разложение функции f (z) в ряд Лорана

(3)

в окрестности изолированной особой точки а. При этом возможны следующие случаи.
1. Главная часть ряда Лорана отсутствует: 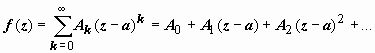. (4)
В этом случае особая точка а называется устранимой.
2. Главная часть содержит конечное число членов: 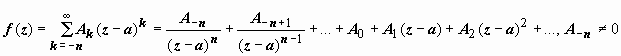. (5)
В этом случае особая точка а называется полюсом n -го порядка. Если n =1, полюс называется простым, в остальных случаях - кратным.
3. Главная часть содержит бесконечно много членов. В этом случае особая точка а называется существенно особой точкой.
Признаки особых точек по значению .
1. Для того, чтобы особая точка z = a была устранимой особой точкой функции f (z), необходимо и достаточно, чтобы существовал конечный предел = C, C ≠ ∞.
Док-во. Выпишем разложение f (z) в ряд Лорана:

.

Очевидно, что может быть конечным тогда и только тогда, когда отсутствуют члены с отрицательными степенями, т.е. отсутствует главная часть, т.е. z = a – устранимая особая точка. В этом случае = A ₀.
2. Для того, чтобы особая точка z = a была полюсом функции f (z), необходимо и достаточно, чтобы существовал бесконечный предел = ∞.
Докажем теорему, из которой следует это утверждение.
Теорема. Для того, чтобы особая точка z = a была полюсом n -го порядка функции f (z), необходимо и достаточно, чтобы в некоторой окрестности этой точки f (z) представлялась в виде , где φ (z) аналитическая в точке а функция, φ (a) ≠ 0.
Док-во. Необходимость. Пусть f (z) имеет в точке z = a была полюс n -го порядка, т.е. 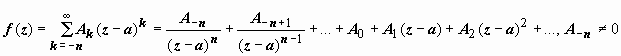. Преобразуем это выражение:

. Обозначим φ (z) сумму ряда, стоящего в скобках:

φ (z) = A _{- n} + A _{- n + 1}(z − a) + A _{- n + 2}(z − a)² + … + A ₀(z − a) ⁿ + A ₁(z − a) ^{n + 1} + A ₁(z − a) ^{n + 2} + ….
Ряд Лорана функции f (z) сходится в некотором кольце 0 < | z – a | < r. Пусть точка z ₁ принадлежит этому кольцу. Ряд для φ (z) сходится в этой точке, так как он отличается от сходящегося ряда для f (z) только постоянным множителем 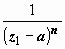; по теореме Абеля ряд для φ (z) сходится в круге | z – a | < | z ₁ – a |, и φ (z) аналитична в этом круге как сумма степенного ряда.
Достаточность. Пусть , где φ (z) аналитическая в точке а функция, φ (a) ≠ 0. Разложим φ (z) в ряд Тейлора:

φ (z) = B ₀ + B ₁(z − a) + B ₂(z − a)² + … + B_k (z − a) ^k + ….

Тогда

, т.е. главная часть ряда Лорана функции f (z) начинается с члена , где B ₀ = φ (a) ≠ 0, т.е. точка z = a – полюс n -го порядка.
Следствие. Точка z = a – полюс n -го порядка функции f (z) тогда и только тогда, когда существует конечный

(6)

Теорема о связи нулей и полюсов. Функция f (z) имеет в точке z = a – полюс n -го порядка тогда и только тогда, когда функция имеет в этой точке нуль n -го порядка.
Это теорема непосредственно следует из доказанной теоремы и теоремы предыдущего раздела. С её помощью легко определять порядок полюса. Так, мы доказали, что функция имеет в точке 0 нуль пятого порядка. Поэтому функция имеет в этой точке полюс пятого порядка.
3. Мы доказали, что в устранимой особой точке и в полюсе существует (конечный или бесконечный) . Поэтому в существенно особой точке этот предел существовать не может. Более того, верна теорема Пикара, которую мы приведём без доказательства:
В любой сколь угодно малой окрестности своей существенно особой точки функция f (z) принимает (причём бесконечно много раз) любое конечное значение (за исключением, возможно, одного).

Вычет аналитической функции в особой точке.

Пусть функция f (z) аналитична в области D за исключением точки a. Разложим f (z) в окрестности этой точки в ряд Лорана: 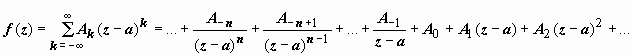(7)
Коэффициент A _-1 называется вычетом функции f (z) в точке а и обозначается .

Если γ - произвольный кусочно-гладкий замкнутый контур, расположенный в области D и содержащий внутри себя точку а, то, согласно общей формуле для коэффициентов ряда Лорана, получаем другое, эквивалентное, определение вычета,

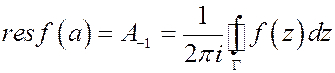. (8)

Дата добавления: 2014-01-07