Вычет в устранимой особой точке равен нулю

Это следует из определения устранимой особой точки: главная часть ряда Лорана отсутствует, все коэффициенты с отрицательными индексами равны нулю, A _-1 = 0.

Вычеты в полюсах.

Если а - простой полюс функции f (z), то

. (9)
Док-во. Простой полюс - полюс первого порядка, поэтому разложение в ряд Лорана начинается с минус первой степени: .

Тогда

(z − a) f (z) = A _-1 + A ₀(z − a) + A ₁(z − a) ² + A ₂(z − a) ³ + …,

.
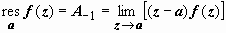Пусть 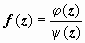, где φ (z), ψ(z) - аналитические в окрестности точки а функции. Если а - простой нуль функции ψ (z), и φ (a) ≠ 0, то

. (10)
Док-во. Если а - простой нуль функции ψ (z), и φ(a) ≠ 0, то а – простой полюс функции

.

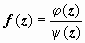Тогда, по предыдущему утверждению, .
Если а - полюс функции f (z) n - го порядка, то

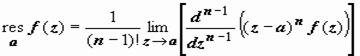. (11)

Док-во. Так как точка z = a - полюс n -го порядка функции f (z), то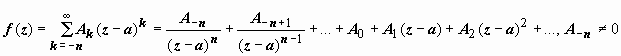

Для того чтобы удалить особенность в точке а, умножим f (z) на

(z – a) ⁿ: (z – a) ⁿf (z) = A _{- n} + A _{- n + 1}(z − a) + … + A _{- 1}(z − a) ^{n - 1} +

+ A ₀(z − a) ⁿ + A ₁(z − a) ^{n + 1} + ….

Теперь, чтобы убрать первые члены этой формулы и добраться до A _-1, дифференцируем это произведение n -1 раз:

, ,
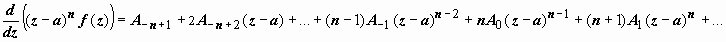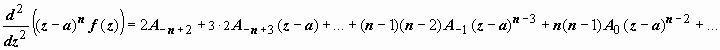, , откуда и следует доказываемая формула.

Вычет в существенно особой точке находится из разложения функции в ряд Лорана.

Примеры нахождения вычетов.
1. .
Эта функция имеет единственную особую точку - z = 0. Функция 1 – cos z при z → 0 - бесконечно малая второго порядка, (1 – cos z)² - четвертого, поэтому можно предположить, что существует конечный , т.е. z = 0 - устранимая особая точка. Доказываем строго: 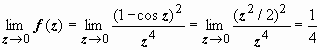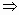z = 0 - устранимая особая точка.
Можно решить эту задачу по-другому. Так как cos z = 1 − z ² /2! + z ⁴ /4! + … + (−1) ⁿz ^{2 n} /(2 n)! + …, то (1 − cos z)² = (z ² /2! − z ⁴ /4! + … + (−1) ^{n + 1} z ^{2 n} /(2 n)! + …)² = z ⁴·(1/2! − z ² /4! + … + (−1) ^{n + 1} z ^{2 n - 2}/(2 n)! + …)², то f (z) = (1/2! − z ² /4! + … + (−1) ^{n + 1} z ^{2 n - 2}/(2 n)! + …)². Понятно, что разложение этой функции по степеням z не будет содержать членов с отрицательными степенями, т.е. z = 0 - устранимая особая точка.
2. .
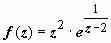Особая точка: z = 2. Разлагаем функцию в ряд по степеням z - 2:
z ² = [(z - 2) + 2] ² = (z - 2)² + 4(z - 2) + 4, , .

Разложение содержит бесконечное количество слагаемых с отрицательными степенями z - 2, следовательно, z = 2 - существенно особая точка.

.
3. f (z) = ctg z.
Особые точки – те, в которых sin z = 0: a_k = k π, k = 0, ±1, ±2, ±3, …. Эти точки являются простыми нулями знаменателя, так как (sin z)′| _{z = ak} = cos z | _{z = ak} = ± 1 ≠ 0. Числитель cos a_k ≠ 0, поэтому точки a_k - простые полюса. Вычеты находим по формуле

:

.
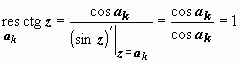4. .
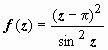Особые точки – те, в которых sin z = 0: a_k = k π. В этих точках предел знаменателя 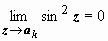; во всех точках a_k, за исключением a ₁ = π, числитель отличен от нуля, поэтому

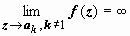, следовательно, эти точки – полюса. Для определения порядка этих полюсов найдём порядок нуля знаменателя: ψ (z) = sin ² z, ψ (a _k) = 0; ψ′ (z) = sin 2 z, ψ′ (a_k) = 0; ψ″ (z) = 2 cos 2 z, ψ′ (a_k) = 2 ≠ 0, следовательно, эти полюса имеют второй порядок (при k ≠ 1). В точке a ₁ = π функция представляет собой неопределённость 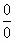, однако, если вспомнить, что sin z = sin(π − z) = − sin(z − π), эта неопределённость раскрывается просто: ,

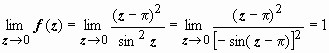т.е. функция имеет конечный предел, следовательно, a ₁ = π - устранимая особая точка.
Вычет в устранимой особой точке равен нулю, поэтому .

В остальных точках применяем формулу 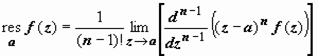при n = 2: 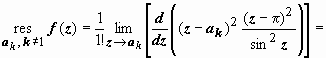(меняем переменную t = z - a_k, sin z = sin(t + a_k) = sin(t + k π) = (-1) ^k sin t) =

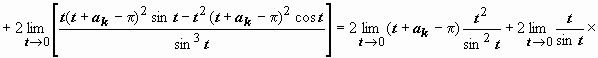
(к последнему пределу применяем правило Лопиталя) .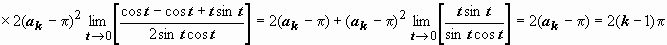

Дата добавления: 2014-01-07