Бесконечно удалённая особая точка

Будем считать точку z = ∞ особой точкой любой аналитической функции.

Мы определили окрестности этой точки как внешности кругов с центром в начале координат: U (∞, ε) = { z ∈ | | z | > ε}. Точка z = ∞ является изолированной особой точкой аналитической функции w = f (z), если в некоторой окрестности этой точки нет других особых точек этой функции. Для определения типа этой особой точки сделаем замену переменной 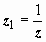, при этом точка z = ∞ переходит в точку z ₁ = 0, функция w = f (z) примет вид . Типом особой точки z = ∞ функции w = f (z) будем называть тип особой точки z ₁ = 0 функции w = φ (z ₁). Если разложение функции w = f (z) по степеням z в окрестности точки z = ∞, т.е. при достаточно больших по модулю значениях z, имеет вид , то, заменив z на , получим . Таким образом, при такой замене переменной главная и правильная части ряда Лорана меняются местами, и тип особой точки z = ∞ определяется количеством слагаемых в правильной части разложения функции в ряд Лорана по степеням z в окрестности точки z = 0. Поэтому
1. Точка z = ∞ - устранимая особая точка, если в этом разложении правильная часть отсутствует (за исключением, возможно, члена A ₀);
2. Точка z = ∞ - полюс n -го порядка, если правильная часть заканчивается слагаемым A _n · z ⁿ;
3. Точка z = ∞ - существенно особая точка, если правильная часть содержит бесконечно много членов.

При этом остаются справедливыми признаки типов особых точек по значению : если z = ∞ - устранимая особая точка, то этот предел существует и конечен, если z = ∞ - полюс, то этот предел бесконечен, если z = ∞ - существенно особая точка, то этот предел не существует (ни конечный, ни бесконечный).

Примеры: 1. f (z) = -5 + 3 z ² - z ⁶. Функция уже является многочленом по степеням z, старшая степень - шестая, поэтому z = ∞ - полюс шестого порядка.
Этот же результат можно получить по-другому. Заменим z на 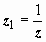, тогда 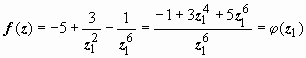. Для функции φ (z ₁) точка z ₁ = 0 - полюс шестого порядка, поэтому для f (z) точка z = ∞ - полюс шестого порядка.
2. . Для этой функции получить разложение по степеням z затруднительно, поэтому найдём : ; предел существует и конечен, поэтому точка z = ∞ - устранимая особая точка.
3. 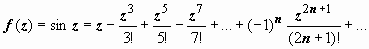. Правильная часть разложения по степеням z содержит бесконечно много слагаемых, поэтому z = ∞ - существенно особая точка. По другому этот факт можно установить исходя из того, что не существует.

Вычет функции в бесконечно удалённой особой точке.

Для конечной особой точки a , где γ - контур, не содержащий других, кроме a, особых точек, проходимый так, что область, им ограниченная и содержащая особую точку, остаётся слева (против часовой стрелке).

Определим 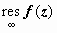аналогичным образом: , где Γ ⁻ - контур, ограничивающий такую окрестность U (∞, r) точки z = ∞, которая не содержит других особых точек, и проходимый так, что эта окрестность остаётся слева (т.е. по часовой стрелке). Таким образом, все остальные (конечные) особые точки функции должны находиться внутри контура Γ ⁻. Изменим направление обхода контура Γ 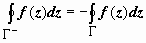⁻: . По основной теореме о вычетах , где суммирование ведётся по всем конечным особым точкам. Поэтому, окончательно,

,

т.е. вычет в бесконечно удалённой особой точке равен сумме вычетов по всем конечным особым точкам, взятой с противоположным знаком.

Как следствие, имеет место теорема о полной сумме вычетов: если функция w = f (z) аналитична всюду в плоскости С, за исключением конечного числа особых точек z ₁, z ₂, z ₃, …, z_k, то сумма вычетов во всех конечных особых точках и вычета в бесконечности равна нулю.

Отметим, что если z = ∞ - устранимая особая точка, то вычет в ней может быть отличен от нуля. Так для функции , очевидно, ; z = 0 - единственная конечная особая точка этой функции, поэтому 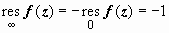, несмотря на то, что , т.е. z = ∞ - устранимая особая точка.

Дата добавления: 2014-01-07