Оборачиваемость

Итак, оба компонента общих затрат, связанных с поддержанием запасов, изменяются обратно пропорционально друг другу, поэтому можно найти, по крайней мере теоретически, такую величину средне­го запаса, которой соответствует минимальный уровень этих затрат. Легче всего логику выявления оптимальной партии заказа предста­вить графически.

Затраты

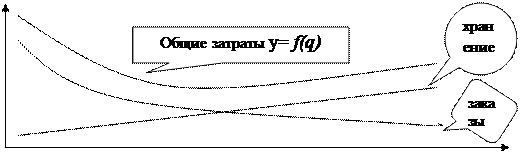
Уровень запасов

Несложно вывести одно из возможных представлений модели уп­равления запасами. Введем обозначения:

q — размер заказываемой партии запасов, ед.;

D — годовая потребность в запасах, ед.;

F — затраты по размещению и выполнению одного заказа (обычно предполагаются постоянными), руб.;

Н — затраты по хранению единицы производственных запасов, руб.;

С_с — затраты по хранению, руб.;

С о — затраты по размещению и выполнению заказа, руб.;

C_t — общие затраты, руб.

Допустим, предприятие придерживается следующей политики: по мере исчерпания запасов поступает очередная партия сырья и матери­алов размером в q единиц. В этих условиях средний размер запасов будет равен q/2, количество заказанных и полученных партий сырья и материалов за год составит D/q, а суммарные затраты по поддержа­нию запасов могут быть найдены по формуле:

C_t = С_с + С₀ = Н * q/2 + F* D/ q;

Как видно из графика, функция затрат y= f(q) имеет вид параболы, поэтому, дифференцируя по q, можно найти такое его значение, при котором функция достигает своего минимума. Таким образом, форму­ла расчета размера оптимальной партии заказа (Economic Order Quantity, EOQ) имеет вид: ЕOQ = √ (2*F*D/H). В рамках этой теории разработаны и схемы управления заказами, позволяющие с помощью ряда параметров формализовать процедуру обновления запасов, в частности, определить уровень запасов, при котором необходимо делать очередной заказ. Одна из таких схем вы­ражается системой моделей: RP = MU*MD; SS = RP- AU*AD; MS = RP + EOQ - LU * LD, где AU — средняя дневная потребность в сырье, ед.; AD — средняя продолжительность выполнения заказа (от момента размеще­ния до момента получения сырья), дн.; SS — наиболее вероятный минимальный уровень запасов (страховой запас), ед.; MS — максимальный уровень запасов, ед.; RP — уровень запасов, при котором делается заказ, ед.; LU — минимальная дневная потребность в сырье, ед.; MU — максимальная дневная потребность в сырье, ед.; MD — максимальное число дней выполнения заказа; LD — минимальное число дней выполнения заказа.

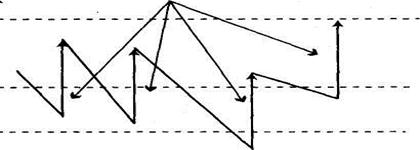
Графическая иллюстрация варьирования величины запасов в ус­ловиях приведенной системы моделей выглядит следующим образом.

EOQ

Запасы, ед.

MS

RP

SS

Рис. Динамика запасов в условиях оптимального управления запасами

Политика управления заказами в этом случае такова. На основе статистики и экспертных оценок рассчитываются значения исходных факторов системы моделей. Как только уровень запасов опускается до величины RP или ниже, делается заказ на поставку сырья и мате­риалов. Если поставка осуществляется максимально эффективно, то уровень запасов в компании может достичь максимальной величины MS. Если после совершения заказа ежедневное потребления сырья и материалов достигло максимума и по каким-либо причинам поставка очередной партии затянулась, компании приходится воспользоваться страховым запасом, т.е. уровень запасов может опуститься ниже вели­чины SS, а при самых неблагоприятных условиях он может быть близ­ким к нулю.

Все приведенные модели в известной степени носят искусствен­ный характер в силу ряда условностей. В частности, затраты по хра­нению обычно имеют нелинейную связь с уровнем запасов, рассчи­тать более или менее приемлемые значения исходных факторов в мо­делях довольно сложно и т.п. Основное предназначение этих моде­лей — помочь в понимании логики систем управления запасами. Тем не менее для крупных компаний они позволяют получить некоторые ориентиры, имеющие практическую значимость.

Для финансового менеджера огромную роль играет и знание прин­ципов анализа эффективности вложений в производственные запа­сы. Не вдаваясь подробно в методику анализа, отметим только, что в ее основе лежит, в частности, понимание методов представления запасов в отчетности. В зависимости от того, какие методы учета запасов (или себестоимости продукции) определены учетной поли­тикой хозяйствующего субъекта, возможна различная оценка средств, вложенных в запасы, а следовательно, и различны значения параметров, участвующих в определении оптимальной политики управления.

Важнейшим элементом анализа запасов является оценка их оборачиваемости. Основной показатель — время обращения в днях, рассчитываемый делением среднего за период остатка запасов на однодневный оборот запасов в этом же периоде. Ускорение оборачиваемо­сти сопровождается дополнительным вовлечением средств в оборот, замедление — отвлечением средств из хозяйственного оборота, их относительно более длительным омертвлением в запасах (или иммобилизацией собственных оборотных средств). Сумма средств, допол­нительно вовлеченных в оборот (или отвлеченных из оборота), рас­считывается по специальной формуле.

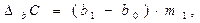
где 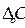— сумма средств, дополнительно вовлеченных в оборот, если ,

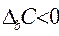либо сумма отвлеченных из оборота средств, если;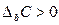

b0 — оборачиваемость запасов в днях в базисном периоде; b1- оборачиваемость запасов в днях в отчетном периоде;

m1-однодневный фактический оборот в отчетном периоде.

Ретроспективный анализ производственных и товарных запасов может выполняться с использованием жестко детерминированных факторных моделей. В частности, одна из моделей, наиболее распространенных в анализе товарных запасов, имеет вид:

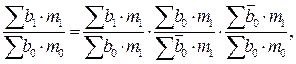(11.5)

где b — время обращения в днях /-й товарной группы; m — однодневный товарооборот /-й товарной фуппы.

Разности между числителем и знаменателем результативного и факторных признаков связаны следующей зависимостью:

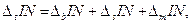
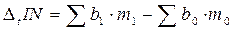— характеризует общее изменение товарных за­пасов за период;

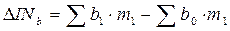— характеризует изменение товарных запасов под влиянием изменения оборачиваемости по от­дельным товарным группам;

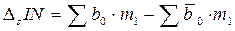— характеризует изменение товарных запасов под влиянием изменения структуры товаро­оборота;

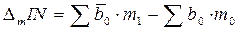— характеризует изменение товарных запасов под влиянием изменения объема товарооборота.

Особому контролю и ревизии должны подвергаться залежалые и неходовые товары, представляющие собой один из основных элемен­тов иммобилизованных (т.е. исключенных из активного хозяйствен­ного оборота) оборотных средств. Эта практика является обыденной не только в России, но и в странах Запада.

При анализе недостач и потерь от порчи товарно-материальных ценностей, не списанных с баланса в установленном порядке, необхо­димо изучить их состав и причины образования, постараться устано­вить конкретных виновников для взыскания с них причиненного ущер­ба. Требуется также проверить: условия хранения ценностей; обеспе­чение их сохранности по количеству и качеству; квалификацию материально ответственных лиц; запущен ли учет товарно-материаль­ных ценностей; соблюдаются ли правила проведения инвентаризаций и выявления их результатов.

Дата добавления: 2014-01-07