Взаимодействие радиоактивных излучений с окружающей средой

Взаимодействие заряженных частиц.

К заряженным частицам относятся α- и β – частицы. α-частица представляет собой ядро гелия (₄He²⁺), масса α-час­тицы составляет 4 а.е.м.(по меркам микромира это огромная величина), заряд - +2.. Масса электрона (позитрона) примерно в 7300 раз меньше массы α-частицы, а заряд β-частицы, равный по модулю заряду электрона, равен ±1. Энергия заряженной частицы – кинетическая энергия, которая пропорцио­на­льна массе частицы и квадрату скорости ее движения.

Будучи электрически заряженными, частицы взаимодействуют с куло­новскими полями ядра и электронов атома вещества. Необходимо отметить, что ядро занимает ничтожно малый объем атома (примерно 10^-12 части объе­ма атома), поэтому вероятность взаимодействия заряженной частицы с куло­новским полем ядра невелика. В результате взаимодействия частицы вызыва­ют ионизацию окружающей среды, т.е. образование положительных ионов и свободных электронов вследствие вырывания электронов из внешних оболо­чек атомов. При ионизации вещества происходит потеря части энергии (ско­рости) заряженной частицы в каждом акте взаимодействия. После некоторого числа взаимодействий энергия (скорость) заряженной частицы уменьшается практически до нуля и происходит ее нейтрализация путем присоединения электронов для α-частицы или присоединения электрона к иону для β-части­цы. Таким образом, при каждом акте взаимодействия происходит замедление частицы, т.е. частица имеет отрицательное ускорение. Известно, что при дви­жении заряженной частицы с ускорением, частица начинает излучать энер­гию, что приводит к потере энергии частицы. Следовательно, при взаимо­дей­ствии заряженной частицы с веществом имеют место быть ионизационные и радиационные потери энергии.

Радиационные потери пропорциональны квадрату ускорения. Учитывая, что ускорение a = F/M, где F – сила, действующая на частицу массой М, получим, что радиационные потери при рассеянии на кулоновском центре пропорциональны (Ze – заряд центра). Отсюда следует, что радиационные потери для α-частицы примерно в 10⁸ раз меньше, чем для β-частицы (т.к. масса α-частицы примерно в 10⁴ раз больше массы электрона). Для β-частицы радиационные потери пропорциональны EZ², а ионизационные – Z, поэтому отношение радиационных потерь энергии Eр к ионизационным Еи оказывается пропорциональным EZ:

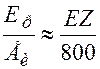
где энергия β-частицы дана в Мэв. Следовательно, для основных породообра­зую­щих элементов (Z = 8 ÷ 20) при значениях энергии β-частицы, харак­тер­ных для естественных радиоактивных элементов 0.1 ÷ 2 Мэв, Еи / Ер > 10. Таким образом, для заряженных частиц характерны ионизационные потери.

Количественными характеристиками потерь энергии частицы служит ве­ли­чина удельных потерь энергии (dE/dx) (т.е. потери энергии на единицу длины пути частицы) и пробег частицы L в веществе (полный путь частицы в веществе).

Линейный пробег в воздухе α-частицы в области энергий 4 Мэв < Eα < 9 Мэв, характерной для естественных радиоактивных элементов, приближен­но выражается: 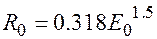и составляет от 2.5 до 9 см. Зная пробег α-частицы в воздухе, легко найти ее пробег в любом другом веществе. На­при­мер, пробег в алюминии R_AL относительно пробега в воздухе R_O можно записать так:

где: ρ – плотность; А – атомный вес. Атомный вес воздуха (28% кислорода и 72% азота) равен 14.4, плотность воздуха 0.0013 г/см³, для алюминия: плот­ность 2.7 г/см³, А равняется 27. Подставляя эти значения, получаем, что про­бег α-частицы в алюминии равен десяткам микрон.

Т.к. масса α-частицы почти на 4 порядка больше массы электрона, то напра­в­ление движения α-частицы при соударении с электронами практичес­ки не меняется.

β-частицы, ввиду малой массы элект­ро­на, при соударении сильно отклоняются от первоначального направления, и их траектория представляет ломанную ли­нию. Поэтому полный максимальный пробег частицы по прямой от начала до конца (эффективный пробег R_m) гораздо меньше длины траектории по ломанной. Величина массового эффективного пробега моноэнергетических электронов (в г/см²) находят по формулам:

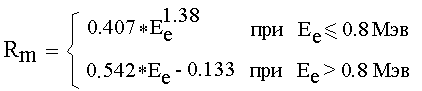
Величина Rm есть массовая толщина такого слоя вещества, необходи­мая для полного поглощения электронов данной энергии. Однако из-за слож­ного характера траекторий пробег большинства электронов в веществе гораз­до меньше Rm. Для сравнения, пробег β-частицы в воздухе составляет, в зависимости от энергии, от единиц до десятков метров.

Удельная потеря энергии оценивается следующим выражением:

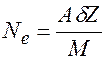
где: N_e – концентрация электронов в веществе; q – заряд частицы; v – скорость движения частицы; A – число Авогадро; δ – плотность вещества; М – атомная масса; Z – заряд ядра.

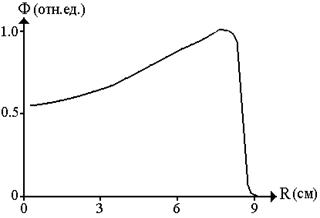
Ионизирующее действие Ф α-части­цы увеличивается по мере прибли­же­ния их к концу пробега R, т.е. с уменьшением скорости. Зависи­мость ионизации, вызываемая α-частицей, зависит от длины пробега R₀:

где Ф – число пар ионов, образованных на пути между рассматриваемой точкой и концом пробега.

Удельная ионизирующая способность β-частицы примерно на порядок ниже, чем у α-части­цы.

Взаимодействие γ-излучения с веществом.

Распространяясь в веществе, γ-кванты взаимодействуют с электронами ядрами атомов, а также с кулоно­вс­ким полем, окружающим электроны и ядра атомов. Имеется возможность осуществления более десятка элементарных процессов взаимодействия γ-излучения с веществом, завершающееся рассеянием или поглощением γ-квантов. Вероятность протекания каждого из этих процессов зависит от энергии γ-кванта, атомного номера Z элемента вещества.

В ядерной геофизике используется γ-излучение с максимальной энер­ги­ей до 3 Мэв. Для такого γ-излучения характерно взаимодействие с электро­нами атомов. Наиболее вероятны: фотоэлектрическое поглощение (фотоэф­фект) на электронах внутренних оболочек атома; поглощение γ-кванта в процессе образования пары электрон – позитрон в кулоновском поле элек­тронов и ядра (рождение электрон - позитрона РЭП); неупругое рассеяние γ-кванта на электронах (эффект Комптона); упругое рассеяние γ-кванта на элек­тронах (эффект Томсона).

I. Рассеяние γ-квантов свободными электронами

Считать электроны свободными, т.е. пренебречь связью электронов в атоме, можно лишь для энергий фотонов, значительно превышающей энер­гию связи электрона ε_е. Энергия связи валентных электронов – величина порядка единиц электрон-вольта (эВ), для электронов внутренних оболочек это значение возрастает, достигая максимума для электронов К-оболочки - от единиц до десятков Кэв (в зависимости от Z – заряда ядра).

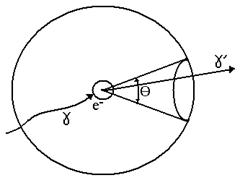При томсоновском рассеянии энергия гамма-кванта до взаимодействия (Еγ) равняется энергии гамма-кванта после взаимодействия (Еγ’), т.е. процесс идет без потери энергии γ-кванта (Еγ = Еγ’).

Томсонов­ское рассеяние преобладает при Еγ << m_ec² (m_ec² = 511 Кэв, m_e – масса электрона, с – ско­рость света), когда энергия γ-кванта сопоста­вима с энергией связи электрона ε_е. Диффе­рен­циальное сечение рассеяния характеризует вероятность рассеяния γ-квантов под данным углом θ на одном электроне. Дифференциальное, по телесному углу, сечение томсоновского рассеяния описывается:

где r₀ – классический радиус электрона r₀=e²/mc² = 2.8_*10^-13 см

Интегральное сечение (вероятность) томсоновского рассеяния на электроне:

_eσ_T = (8/3)πr₀² = 0.66*10^-28 м²/электрон

Комптоновское рассеяние соответствует случаю неупругого рассеяния γ-кванта на свободном электроне, когда в результате взаимодествия рассеян­ный γ-квант имеет меньшую энергию, чем первичный (Еγ > Eγ’). Возникает в тех случаях, когда энергия γ-квантов значительно превосходит энергию связи электрона в атоме (Еγ > ε_е), в области энергий 0.05 < Еγ < 10 Мэв комптон-

эффект является преобладающим видом взаимодействия γ-квантов с вещест­вом. Разность энергий Еγ - Eγ’ уносится электроном, ко­торый получает кине­тическую энер­гию Pe.

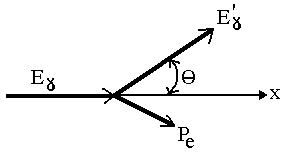
Из этого выражения следует, что макси­мальная энергия гамма-кванта, после рассеяния на электроне, при θ = 0, а минимальная – при θ = 180⁰.

Микросечение комптоновского рас­сеяния σ_k при малых энергиях рас­тет, а затем медленно уменьшается с увеличени­ем энергии γ-квантов. Для легких эле­ментов (Z < 20), кроме во­до­рода, макроскопическое сечение μ_к комп­то­новского рассеяния не зави­сит от Z и пропорционально плотности вещества δ. Действительно, число атомов в 1 см³ вещества N = δ*A/M (А – число Авогадро, М – атомная масса вещества), следовательно μ_k =N*σ_k = AδZσ_k/M. Учитывая, что для легких элементов Z/M ≈ 0.5, получаем μ_k = Aδσ_k/2.

II. Поглощение γ-квантов электронами атомов

Фотоэффект. Фотоэффектом называется такой процесс взаимодейст­вия γ-кванта с электроном, при котором электрону передается вся энергия γ-кванта. При этом электрон выбрасывается за пределы атома с кинетической энергией Ее = Еγ – Ii где Еγ – энергия γ-кванта; Ii – потенциал ионизации i-оболочки атома. Осво­бо­дившийся в результате фотоэффекта место на электронной оболочке запол­няется электронами с вышерасположенных орбит. Этот процесс сопровожда­ется испусканием характеристического рентгеновского излучения, либо ис­пу­­с­канием электронов Оже.

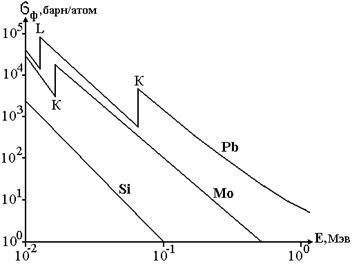Чем меньше энергия связи электрона с атомом, по сравнению с энер­гией γ-кванта, тем менее вероятен фотоэффект. Это обстоятельство опреде­ляет все основные свойства фотоэффекта: ход сечения в зависимости от энергии γ-кванта; соотношение вероятности (сечения) фотоэффекта на разных электронных оболочках атома; зависимость сечения от Z вещества.

Вероятность фотоэффекта тем больше, чем меньше разность энергий потенциала ионизации i-оболочки и энергией γ-кванта. Для γ-кванта с энер­ги­ей, значительно превышаю­щей энергию связи электрона с атомом, электрон оказывается свободным и фотоэффект ста­но­вится маловероятным, более вероятно комптоновское рассе­яние. По мере убывания Еγ сечение фотоэффекта возрас­тает. Рост σ_ф продолжается до тех пор, пока Еγ не станет равной потенциалу ионизации I_K (энергии связи) К-оболочки. Начиная с Еγ > I_K, фотоэффект на К-оболочке становится невоз­можным и сечение фотоэффекта определяется только взаимодействием γ-квантов с электронами L-оболочки, далее М-оболочки и т.д. Но электроны этих оболочек связаны с атомом слабее, чем электроны К-оболочки. Поэтому при равных Еγ вероятность фотоэффекта электрона с L-оболочки (а тем более с М-оболочки) существенно меньше, чем с К-оболочки. В связи с этим на кривой сечений фотоэффекта наблюдается резкий скачок при переходе с К-оболочки на L-оболочку.

Для одного и того же вещества для К-оболочки ход сечения фотоэф­фек­та приблизительно оценивается:

при Е_γ > I_K σ_ф ≈ 1/ Е_γ^3.5;

при Е_γ >> I_K σ_ф ≈ 1/ Е_γ.

Вероятность (сечение) фотоэффекта очень резко зависит от вещества (заряда Z атома), на котором происходит фотоэффект: σ_ф ≈ Z⁵. Это объясня­ет­ся различной энергией связи электрона в различных веществах. В легких элементах, при Z < 25, электроны связаны кулоновскими силами относи­тель­но слабее, чем в элементах с Z > 50 (тяжелые элементы).

Образование (рождение) электронно-позитронных пар (РЭП). Процесс образования пар состоит в том, что вся энергия кванта в кулоновском поле ядра или элек­трона передается образующей паре электрон-позитрон. Энергия покоя пары равна 2m_еc² = 1022 Кэв, которая совпадает с пороговой энергией γ-кванта, при которой начинается РЭП в поле ядра. При образовании пары в кулонов­ском поле электрона пороговая энергия γ-кванта повышается до 4m_еc² = 2044 Кэв. Учитывая, что в ядерной геофизике используются γ-кванты с энергией до 3 Мэв, роль РЭП при поглощении γ-квантов пренебрежимо мала.

Поглощение γ-кванта в процессе РЭП сопровождается вторичным про­цессом. Возникший при поглощении γ-кванта позитрон замед­ляется и, соеди­ня­ясь с одним из электронов среды, аннигилирует. При этом образуются два аннигиляционных γ-кванта с энергией 511 Кэв каждый, разлетающиеся в противоположные стороны.

Характеристическое излучение элементов.

В результате фотоэффекта эле­к­трон выбрасывается за пределы атома, т.е. происходит ионизация атома. Поскольку электроны, окружающее атомное ядро, находятся на определен­ных энергетических уровнях (K, L, M и т.д.), при удалении одного из элект­ронов, образуется вакансия и атом оказывается в возбужденном состоянии. Всякое возбужденное состояние энергетически неустойчиво и через очень короткий промежуток времени (от 10^-16 до 10^-7 сек) происходит заполнение образовавшейся вакансии электроном с более удаленного уровня, понижая возбуждение. Разность энергий, между уровнями с которого электрон пере­шел на другой, высвобождается испусканием фотона характерис­ти­ческого излучения. Так как энергетические уровни электро­нных оболочек для каж­дого вещества имеют строго фикси­рованные значения, то и энергия излуче­ния фотона для каждого элемента строго фиксирована (характерна).

Согласно квантовой теории, элек­троны в атоме располагают­ся на стационарных орбитах, за­полнение которых идет с орби­ты с минимальным уровнем энергии. Для характеристик этих энергетических уровней служат так называемые кванто­вые числа: n – главное кванто­вое число, равное 1, 2 …. 0;

l – орбитальный момент, l = n-1, n-2 … 0; m_L – магнитный мо­мент, m_L = ±‌‌‌│l│, = ±‌‌‌│l-1│...0; s – спиновое число, равно ±1/2.

Разрешен переход с уровня на уровень при выполнении условия Δm_L = ±1.

Характеристическое излучение, испускаемое атомами, имеет линейча­тый дискретный спектр, который состоит из нескольких групп или серий линий (K-, L-, M-серии и т.д.). Наиболее высокоэнергетичной (до нескольких десятков Кэв) является К-серия, далее, в порядке уменьшения, следуют L-серия (до 10 Кэв), M-серия (до 1 Кэв) и т.д.

Излучение К-серии возникает при переходе электрона с более удален­ного уровня на К-уровень, при этом энергия испускаемого кванта равна раз­ности энергий уровня, из которого вышел электрон и К-уровня. В том случае, когда появляется вакансия на L-уровне, возникают линии спектра L-серии. При этом неважно, удален ли электрон с L-уровня вследствие внешних при­чин (фотоэффекта) или в результате перехода электрона с L-уровня на К-уро­вень. Если атомы данного элемента испускают линии К-серии, то при нали­чии возможности, в спектре всегда будут присутствовать линии L-серии.

Спектры характеристического излучения данной серии для различных элементов одинаковы по структуре, то есть по числу и взаимному расположе­нию линий, и отличаются друг от друга только энергией. Наименьшее число линий имеет К-серия (α₁, α₂, β₁, β₂), причем Eβ₂ > Eβ₁ > Еα₁ > Eα₂ . В связи с тем, что вероятность переходов электронов с уровня на уровень разная, при возбуждении большого количества фотонов всех линий К-серии, интенсив­ность их будет различной. Соотношение интенсивностей К-серии для одного и того же вещества такова: Кα₁: Kα₂: Kβ₁: Kβ₂ ≡ 100: 50: 25: 5. Аналогич­ные условия выполняются и для L-серии: Lα_1-2: Lβ_1-4: Lγ ≡ 100: 80: 9.

При заполнении вакансии электроном с более высокого уровня не всег­да возникает фотон характеристического излучения. В некоторых случаях избыток энергии атома может уноситься не фотоном, а электроном (эффект Оже). Такой переход между двумя состояниями атома называется безрадиа­цион­ным и его можно рассматривать как внутриатомное поглощение харак­теристического излучения. Если с К-уровня удален электрон, то возникаю­щий фотон характеристического излучения обладает энергией, достаточной для возбуждения L-уровня. В результате такого внутриатомного фотоэффек­та фотон К-серии поглощается и атом испускает L-электрон (оже-электрон). L-уровень оказывается в состоянии двойной ионизации и атом переходит в нормальное состояние путем излучения фотона L-серии или безрадиацион­ным путем, с испусканием еще одного электрона с более удаленного уровня.

Эффект Оже конкурирует с процессом образования фотонов характери­с­ти­ческого излучения и приводит к снижению выхода характеристического излучения (Х.И.). Отношение числа атомов, испустивших Х.И. (Nq_x) к обще­му числу атомов, возбужденных на q-уровень (Nq) определяет коэффициент выхода Х.И. для q-уровня: Wq = Nq_x / Nq. Приблизительное значение этого коэффициента можно найти по эмпирической формуле:

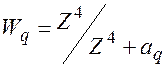
где a_q для К-серии равно a_K = 1.06*10⁶, для L-серии a_L = 10⁸. Таким образом эффект Оже более существенен для легких элементов (Z < 20), и для L-уров­ня коэффициенты выхода Х.И. в несколько раз меньше, чем для К-уровня.

Полное сечение взаимодействия γ-излучения с веществом.

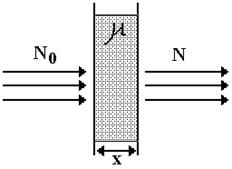Элементар­ные процессы взаимодействия γ-квантов с веществом не зависят друг от дру­га, поэтому полное сечение взаимодействия равно сумме трех сечений: μ = σ_к + σ_т + σ_ф, где индексы к, т, ф относятся, соответственно, к комптоновскому и томсоновскому рассеяниям и фотоэффекту. μ называют коэффициентом ос­ла­б­ления γ-излучения. Его размерность равна обратной длине (см^-1).

Для плоскопараллельного пучка γ-квантов, испытывающих однократное взаимодействие, справедливо выражение N=N₀exp(-μx), где N₀ – кол-во γ-квантов до взаимодействия, N – после взаимодействия, μ – коэффициент ослабления, характеризующий поглощающие свойства среды, х – толщина поглотителя. Значение μ возможно рассчитать через параметры среды:

,

где ρ – плотность, N_A – число Авогадро, А – атомный вес среды, Z – порядко­вый номер элемента в таблице Менделеева, σ_ф – сечение фотоэффекта и σ_к – сечение комптоновского рассеяния. Так как μ пропорционально плотности, иногда удобнее рассматривать массовый коэффициент ослабления к, равный k = μ / ρ. Для сложной среды массовый коэффициент ослабления γ-излучения равен:

где i – количество компонент (элементов) среды, p_i – весовая доля каждой компоненты, k_i – коэффициент ослабления i-компоненты.

Выше было показано ослабление γ-излучения в случае однократного взаимодействия. В реальных средах такое допущение очень грубое, поэтому расчет ослабления потока γ-квантов ведется по функции Кинга. Функция Кинга табулирована и представлена в справочниках.

Дата добавления: 2014-01-07