Исследование модели парной линейной регрессии

а). Параметр 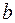называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

b). Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный

коэффициент корреляции , который можно рассчитать по следующим формулам:

. .

Чем ближе абсолютное значение к единице, тем сильнее линейная связь между факторами (при имеем строгую функциональную зависимость). Но следует иметь в виду, что близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.

c). Коэффициент детерминации ² ( используетсядля оценки качества подбора линейной функции 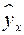) характеризует долю дисперсии результативного признака 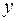, объясняемую регрессией, в общей дисперсии результативного признака:

,

где , .

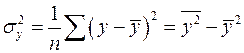Величина характеризует долю дисперсии 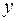, вызванную влиянием остальных, не учтенных в модели, факторов.

После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

d). Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:

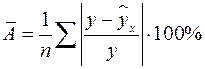. Средняя ошибка аппроксимации не должна превышать 8–10%.

e). Оценка значимости уравнения регрессии в целом производится на основе 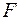-критерия Фишера

, , .

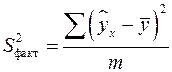Фактическое значение 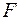-критерия Фишера сравнивается с табличным значением при уровне значимости 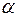и степенях свободы и . При этом, если фактическое значение 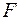-критерия больше табличного, то признается статистическая значимость уравнения в целом.

f). В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: и .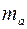

Стандартная ошибка коэффициента регрессии определяется по формуле:

,

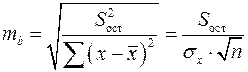где 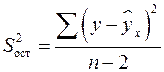– остаточная дисперсия на одну степень свободы.

Величина стандартной ошибки совместно с -распределением Стьюдента при 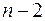степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.

Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение -критерия Стьюдента: которое затем сравнивается с табличным значением при определенном уровне значимости 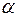и числе степеней свободы . Доверительный интервал для коэффициента регрессии определяется как . Поскольку знак коэффициента регрессии указывает на рост результативного признака 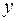при увеличении признака-фактора 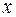(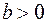), уменьшение результативного признака при увеличении признака-фактора (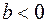) или его независимость от независимой переменной () (см. рис. 1.3), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, 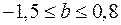. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.

Стандартная ошибка параметра 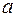определяется по формуле:

. Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется -критерий: , его величина сравнивается с табличным значением при 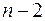степенях свободы.

Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции :

. Фактическое значение -критерия Стьюдента определяется как .

Существует связь между -критерием Стьюдента и 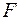-критерием Фишера:

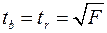. (1.15)

В прогнозных расчетах по уравнению регрессии определяется предсказываемое 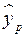значение как точечный прогноз 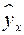при , т.е. путем подстановки в уравнение регрессии 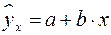соответствующего значения 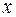. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки 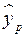, т.е. , и соответственно интервальной оценкой прогнозного значения :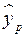

,

где , а – средняя ошибка прогнозируемого индивидуального значения:

.

Требования к качеству оценок параметров: Теория статистического оценивания качество оценок определяет по свойствам несмещенности, эффективности, асимптотической несмещенности и асимптотической эффективности, состоятельности и некоторым другим. Напомним, что оценка является несмещенной, если истинное значение параметра можно рассматривать как ее математическое ожидание или, иначе, математическое ожидание ошибки оценки D a_i должно быть равно нулю:

M [ a _i ]= a _i, M [D a _i ]=0. (1.48)

Оценка рассматривается как эффективная, если она характеризуется наименьшей дисперсией (дисперсия ошибки оценки минимальна) среди всех других аналогичных оценок, полученных различными методами, способами.

– дисперсия оценки, полученной с использованием j -го метода оценивания.

Часто свойство несмещенности выполняется лишь с некоторой степенью «приблизительности» при достаточно больших объемах выборочных данных (при большом числе измерений Т), в пределе при Т ®¥. В этом случае говорят, что оценки являются асимптотически несмещенными. Иногда асимптотическая несмещенность рассматривается в “вероятностном” смысле, т. е. предполагается, что для произвольно малых положительных чисел x и h, в общем случае зависящих от Т, существует такой объем исходных данных Т ₀, что для всех Т > Т ₀ имеет место следующее неравенство:

Дата добавления: 2014-01-07