Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии

Относительно векторов объясняющих переменных (факторов) (столбцов матрицы Х).

При использовании критериев Фишера и Стьюдента считают: остатки 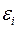– представляют собой независимые случайные величины и их среднее значение равно 0 ( М(e_i) =0 ); они имеют одинаковую (постоянную) дисперсию (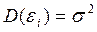) и подчиняются нормальному распределению ().

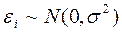1). Нарушение предпосылок относительно случайной составляющей .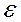

Возможны следующие нарушения предпосылок, если 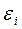зависит от :

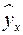1) остатки 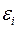не случайны (рис. 2.2а);

2) остатки 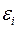не имеют постоянной дисперсии (рис. 2.2б);

3) остатки 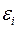носят систематический характер (рис. 2.2в).

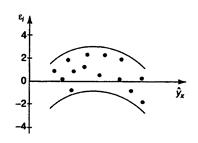
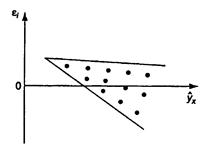
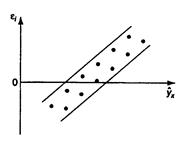
Рис. 2.2. Зависимость случайных остатков 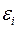от теоретических значений .

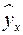В этих случаях необходимо:

- либо применять другую функцию, т.е. изменить спецификацию модели;

- либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки 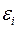не будут случайными величинами.

Нарушение предпосылки 1 (Х- детерминированная матрица):

- стохастическиефакторы, статистически не зависят от регрессионных остатков и оцениваемых параметров;

- стохастические факторы, коррелированны с остатками;

- стохастические факторы и результирующая переменные могут быть измерены только со случайными ошибками.

1). Факторы статистически не зависят от регрессионных остатков и оцениваемых параметров МНК – оценки состоятельные и несмещенные, т.е. на качество оценок это нарушение не влияет.

2). Факторы (объясняющие переменные) коррелированны с регрессионными остатками – проблема эндогенности (нарушается предпосылка М ( Хe ) =0 )

МНК – оценки не являются состоятельными и несмещенными, т.е. на качество оценок это нарушение влияет.

Причины эндогенности:

- ошибки измерения значений факторов;

- невключение в модель значимых факторов;

- проблема «одновременного влияния».

Предпосылка 2 ( М(e_i) =0 ) относительно нулевой средней величины остатков означает, что .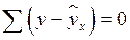

Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.Предпосылка 2 – не нарушается никогда, если в регрессионное уравнение включен свободный член 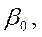т.е. уравнение имеет вид

.

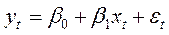При 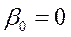оценки параметров – смещенные, коэффициенты детерминации – бессмысленные.

Вывод: включать свободный член.

Предпосылка 3. В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была постоянной (гомоскедастичность). Это значит, что для каждого значения фактора 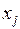остатки 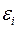имеют одинаковую дисперсию.

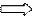Нарушение предпосылки 3 (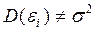) – гетероскедастичность

параметры регрессии не являются оценками с наименьшей дисперсией, т.е. – не эффективные, хотя и несмещенные. Смещенными будут стандартные ошибки и дисперсии, что влечет неверные выводы о значимости параметров.

Тесты на гетероскедастичность: Уайта, тест ранговой корреляции Спирмена, тест Голдфелда—Квандта, тест Глейзера.

Устранение гетероскедастичности – ОМНК.

1). Если, например,в уравнении

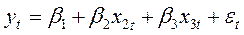
дисперсия связана с некоторой переменной z_t зависимостью.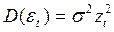, то каждый член регрессионного уравнения делят на z_t. В новом уравнении дисперсия остатков u_t = 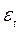/ z_t – постоянная величина, т.е. остатки гомоскедастичны:

D ( u_t ) = D( 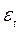/ z_t)=D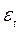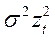( )/z_t²= /z_t²= .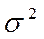

2). Перевести все переменные в логарифмическую форму (если они положительны).

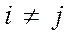3). Использовать специальные робастные методы оценки параметров, когда получаемые оценки в наихудшем случае имеют наименьшую дисперсию. (Робастность – свойство статистической оценки незначительно реагировать на возможные отклонения от рассматриваемой модели).

Предпосылка 4 ( cov (e_i, e_j) = М(e_i e_j)=0 при ) -о независимости остатков. Нарушение предпосылки 4 называется автокорреляцией остатков. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений.

Следствие – проверка статистической значимости оценок параметров ненадежна из-за невозможности достоверной оценки стандартных ошибок.

Тесты на автокорреляцию: тест Дарбина – Уотсона, тест Бреуша – Годфри, тест Льюинга – Бокса.

Устранение автокорреляции– ОМНК.

Для применения ОМНК нужно специфицировать модель автокорреляции регрессионных остатков. В качестве такой модели используется AR(1) – авторегрессионный процесс первого порядка:

,

.

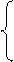
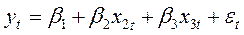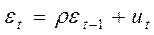Предполагая, что структура модели постоянна, для периода t – 1 имеем:

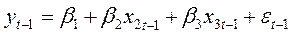
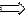
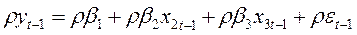
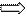
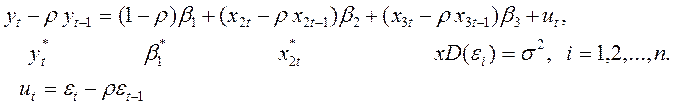
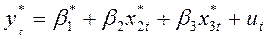
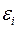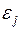Соблюдение третьей и четвертой предпосылок, т.е. отсутствие автокорреляции остатков (они распределены независимо друг от друга), является необходимым условием для получения состоятельных МНК - оценок параметров регрессии. Коэффициент корреляции между и , где 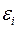– остатки текущих наблюдений, 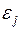– остатки предыдущих наблюдений (например, 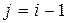), может быть определен как

,

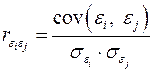т.е. по обычной формуле линейного коэффициента корреляции. Если этот коэффициент окажется существенно отличным от нуля, то остатки автокоррелированы и функция плотности вероятности 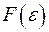зависит от 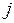-й точки наблюдения и от распределения значений остатков в других точках наблюдения.

При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный метод наименьших квадратов заменять обобщенным методом наименьших квадратов, т.е. методом ОМНК.

Обобщенный метод наименьших квадратов применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии.

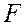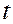Предпосылка 5 о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью - и -критериев. Вместе с тем, оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т.е. при нарушении пятой предпосылки МНК.

Дата добавления: 2014-01-07