Вращение вокруг проецирующих осей

Способ вращения

Сущность этого способа заключается в том, что при вращении вокруг некоторой неподвижной прямой, называемой осью вращения, каждая точка вращаемого геометрического образа перемещается в плоскости, перпендикулярно оси вращения, описывая в ней окружность, радиус которой равен расстоянию точки от оси вращения.

Рассмотрим вращение точки вокруг оси, перпендикулярной к плоскости проекций p₁ (рис. 5.6). Точка А повернута вокруг оси i ^p₁ на угол j°. Плоскость вращения точки параллельна плоскости проекций p₁, радиус вращения AC и траектория вращения точки проецируется на плоскость проекций p₁ в истинном виде. Горизонтальной проекцией является окружность l, фронтальная проекция окружности – отрезок прямой линии, совпадающий с проекцией r.

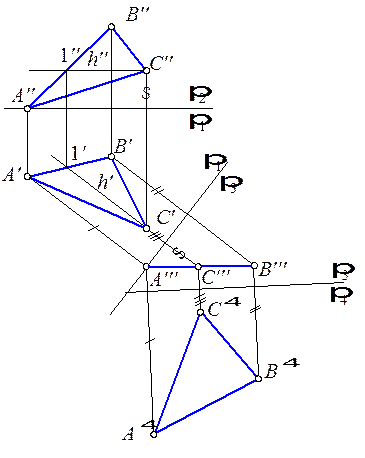
Рис. 5.5

Поворот может быть осуществлен в двух направлениях, указанных стрелками, что дает два новых положения точки – ` А <sub>1</sub> и ` А ₂.

На рис. 5.7 точка В повернута вокруг фронтально проецирующей оси i на угол j°. В этом случае плоскость вращения точки В – фронтальная, и траектория проецируется на фронтальную плоскость проекций окружностью.

Если требуется повернуть прямую на заданный угол, необходимо повернуть на этот угол две ее точки.

На рис. 5.8 на данной прямой а взяты произвольные точки А и В и повернуты на заданный угол j° вокруг вертикальной оси i. В новом положении прямая пройдет через точки ` А и ` В.

На рис. 5.9 аналогично прямая а повернута вокруг фронтально проецирующей оси. В этом примере точка A имеет наименьший радиус вращения (i ²А²^ a ²).

Способом вращения вокруг оси можно привести прямую линию или плоскость в удобное для решения задач положение.

Рассмотрим главные задачи преобразования. Применим прием вращения прямой для определения истинной длины отрезка прямой и величин углов его наклона к плоскостям проекций.

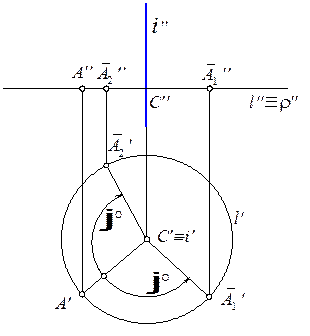
Рис. 5.6 Рис. 5.7

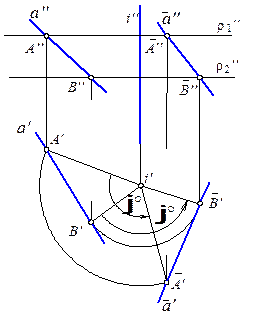
Рис. 5.8 Рис. 5.9

Повернем отрезок прямой общего положения АВ (рис. 5.10) вокруг вертикальной оси i _1, проведенной через точку В до положения, параллельного фронтальной плоскости проекций. Такое положение отрезка характеризуется параллельностью его горизонтальной проекции оси проекций х. Фронтальная проекция отрезка В ², соответствующая новому положению его горизонтальной проекции, выразит истинную длину данного отрезка АВ, а угол a - его наклон к горизонтальной плоскости проекций.

Для определения величины угла наклона того же отрезка АВ к фронтальной плоскости проекций (рис. 5.11) его придется повернуть вокруг оси i₂, перпендикулярной плоскости проекций p₂ до положения, параллельного плоскости проекций p₁. При таком положении отрезка его фронтальная проекция А ²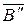должна быть расположена параллельно оси проекций х и тогда горизонтальная проекция отрезка 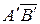выразит его истинную длину, а угол b – его наклон к фронтальной плоскости проекций.

Рис. 5.10 Рис. 5.11

Чтобы преобразовать прямую общего положения в проецирующую, требуется произвести два вращения: первое, преобразующее данную прямую линию в линию уровня, второе – преобразующее полученную линию уровня в проецирующую прямую.

На рис. 5.12 отрезок АВ прямой общего положения преобразован в горизонтальный отрезок 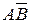вращением вокруг оси i ₁, а затем отрезок A 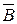преобразован во фронтально проецирующий вращением вокруг оси i ₂.

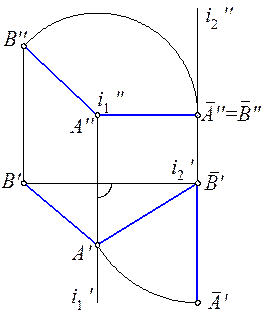
Рис. 5.12

Преобразование плоскости общего положения в проецирующую можно осуществить вращением и вокруг горизонтально проецирующей и вокруг фронтально проецирующей осей.

Чтобы преобразовать плоскость общего положения в плоскость уровня, требуется произвести два вращения: первое – преобразующее данную плоскость в проецирующую; второе – преобразующее полученную проецирующую плоскость в плоскость уровня.

На рис. 5.13 в плоскости a(АВС) проведена горизонталь h (C 1). Ось вращения i ₁ проходит через точку С. Произведено вращение горизонтали до фронтально проецирующего положения . Затем осуществлен поворот на тот же угол, что и горизонтали, точек В и А. Плоскость a (АВС) стала фронтально проецирующей.

Затем плоскость a (АВС) преобразована в горизонтальную плоскость a. Второе вращение производится вокруг оси i ₂ и приводит к горизонтальному положению плоскости.

Дата добавления: 2014-01-07