Точки и линии на кривой поверхности

Краткая классификация кривых поверхностей

КРИВЫЕ ПОВЕРХНОСТИ

Кривая поверхность – это совокупность всех положений некоторой линии движущейся в пространстве. Движущаяся линия называется образующей поверхности, а линии, определяющие закон ее перемещения, направляющими. Образующая может быть кривой и прямой. Поверхность, образуемая движени­ем прямой линии, называется линейчатой, а движением криволинейной образу­ющей – нелинейчатой поверхностью. На рис. 6.1 линейчатая поверхность обра­зована движением прямой образующей l, постоянно проходящей через точку V и во всех своих положениях пересекающей некоторую направляющую m. Эта поверхность называется конической. На рис. 6.2 линейчатая поверхность образована движением образующей l по направляющей m. Такая поверхность называется цилиндрической. Из нелинейчатых поверхностей рассмотрим поверхности, образованные вращением некоторой линии (образующей) вокруг прямой. Такие поверхности называются поверхностями вращения.

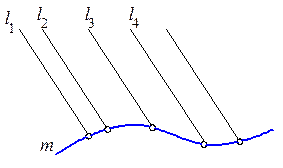
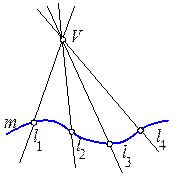
Рис. 6.1 Рис. 6.2

На рис. 6.3 поверхность образована вращением кривой линии l вокруг оси i, лежащей в плоскости этой кривой. Каждая точка М кривой описывает окружность m, называемую параллелью. Параллель наибольшого диаметра называется экватором, наименьшего – горлом. Кривую линию, получающуюся от пересечения поверхности вращения плоскостью, проходящей через ось, называют меридианом. На рис. 6.3 меридианом будет образующая кривая l.

Образующая может быть и прямой линией и кривой, плоской и пространственной.

На рис. 6.4 показано образование поверхности, называемой циклической. Она представляет собой совокупность последовательных положений окружности переменного радиуса, центр которой перемещается по некоторой направляющей m.

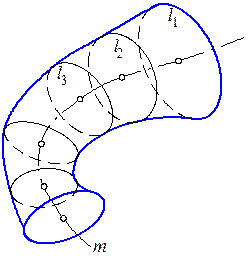
Рис. 6.3 Рис. 6.4

На чертеже изображаются линии и точки, определяющие данную поверхность и линии очерка проекции. Очерковые линии являются на чертеже границами поверхности и разделяют поверхность на видимую и невидимую части.

Цилиндрическая поверхность задана на рис. 6.5 направляющей линией m и образующей l. На фронтальной проекции показаны очерковые образующие l ₁ и l ₂, а на горизонтальной – l ₃ и l ₄.

Точка принадлежит поверхности в том случае, когда она находится на линии этой поверхности.

Точка, принадлежащая поверхности цилиндра, определяется с помощью проходящей через нее образующей. На рис. 6.5 точка А лежит на образующей l. Образующая l проходит через точку В, которая находится на видимой спереди части линии m, поэтому на фронтальной проекции она видна. Следовательно, там же видна и точка А ². На горизонтальной проекции точка В не видна, значит невидимы образующая l и лежащая на ней точка А ¢.

Рис. 6.5

На рис. 6.6 коническая поверхность определена вершиной V и направляющей m. Очерковые образующие на фронтальной проекции - l ₁ и l ₂. Точка А, принадлежащая поверхности, задана с помощью образующей l этой поверхности. Точка А на этой поверхности определяется также и с помощью параллели n.

Фронтальная проекция точки А - А ¢¢ является проекцией двух точек на горизонтальной проекции - А ¢₁, лежащей на видимой половине конуса и А ¢₂, лежащей на невидимой ее половине.

Рис. 6.6

На рис. 6.7 задана поверхность сферы. Линией очерка его фронтальной проекции служит главный меридиан l, и линией очерка горизонтальной проекции – экватор m. Точка А на поверхности сферы определяется с помощью параллели m ₁, причем фронтальной проекции А" на горизонтальной проекции соответствуют точка А ¢₁ на видимой спереди половине сферы и А ¢₂ на невидимой части. Показанная на чертеже точка В лежит на экваторе сферы, а точка 1 – на главном меридиане l.

Рис. 6.7

На рис. 6.8 задана поверхность тора. Она образована вращением образующей окружности l вокруг вертикальной оси i, лежащей в плоскости этой окружности s. Если ось вращения не пересекает образующей окружности, поверхность называют открытым тором (круговым кольцом).

Рис. 6.8

Центр образующей окружности l тора перемещается по окружности, называемой центровой окружностью тора (направляющая кривая). Очерком фронтальной проекции служат главный меридиан, состоящий из двух образующих окружностей, и две параллели – m ₃ и m ₄. Очерком горизонтальной проекции служат экватор m ₁ и горло m ₂ – наибольшая и наименьшая параллели.

Точка на поверхности тора определяется с помощью проходящей через нее параллели. На рис. 6.8 фронтальной проекции А" точки А на гори­зонтальной проекции может соответствовать любая из четырех точек - А ¢₁, А ¢₂, лежащих на параллели m ₅, и А ¢₃ или А ¢₄, лежащих на параллели m ₆. Точки 1 и 2 лежат на главном меридиане тора, точка В – на экваторе.

Если ось касается образующей окружности (рис. 6.9, а), поверхность называют закрытым тором, а в случае, когда ось пересекает окружность – пересекающимся тором (рис. 6.9, б). Пересекающийся тор может быть разделен на две самостоятельные части – внешнюю и внутреннюю.

Кроме рассмотренных, назовем еще несколько поверхностей вращения:

- при вращении эллипса вокруг одной из его осей – большой или малой образуется поверхность – эллипсоид вращения, вытянутый или сжатый;

- при вращении параболы вокруг ее оси образуется поверхность – пара­болоид вращения;

- при вращении гиперболы вокруг ее действительной оси образуется поверхность – двухполостный гиперболоид вращения, а при вращении гипер­болы вокруг ее мнимой оси – однополостный гиперболоид вращения.

Рис. 6.9

Дата добавления: 2014-01-07