Многоканальная система массового обслуживания с ожиданием в очереди при ограничении длины очереди

Рассмотрим теперь другой вид системы массового обслуживания, когда прибывшая заявка в случае, если все каналы к моменту ее прибытия заняты, не покидает станцию, а становится в очередь. Однако заявка может стать в очередь только при условии, что имеется место для ожидания. В противном случае заявка покидает очередь. Порядок вычисления числовых характеристик функционирования системы массового обслуживания для заданных условий следующий. Предположим, что система имеет в своем распоряжении n каналов и m - мест для ожидания в очереди. После того, как все места для ожидания в очереди заняты, прибывшая заявка получает отказ и немедленно покидает очередь (рис. 3). Из графа состояний системы (рис. 3) видно, что, включая состояние Х_n очереди нет. Затем возникает очередь. Из графа состояний видно также» что поток, переводящий систему слева направо, определяется плотностью 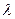. Что же касается потока событий, переводящего систему справа налево, то до возникновения очереди он равен 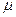, , 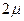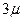... . 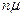После возникновения очереди указанный поток остается постоянным и равным .

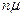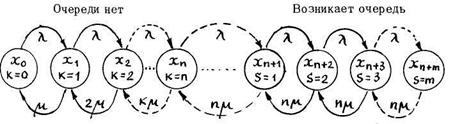
Рис.3. Граф состоянии многоканальной системы массового обслуживания с ожиданием в очереди с ограничением длины очереди (S — число занятых мест)

Пользуясь правилом "Что втекает, то и вытекает", можно вычислить вероятности состояний системы (табл. 2 и 3).

Сумма вероятностей всех состояний системы должна быть равна единице, т.е.

.

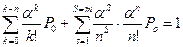Откуда

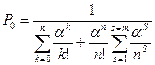
Таблица 2. Вероятности состояний многоканальной системы массового обслуживания, с ожиданием в очереди при ограничении длины очереди до возникновение очереди

Число занятых каналов «К»	Приведенное правило: «что вытекает, то и втекает»	Вероятности состояний для многоканальной системы с отказами
.	.	.
.	.	.
.	.	.
.	.	.
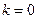
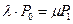
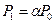
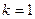
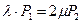
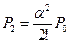
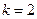
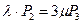
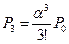
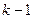
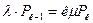
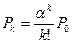
k=n-1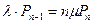

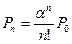
Таблица 3. Вероятности состояний многоканальной системы массового обслуживания, с ожиданием в очереди при ограничении длины очереди после возникновения очереди

Число занятых мест «S»	Приведенное правило: «что вытекает, то и втекает»	Вероятности состояний для многоканальной системы с отказами
.	.	.
.	.	.
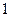
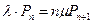
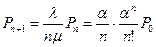
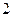
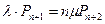
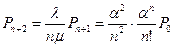
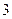
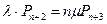
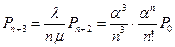
S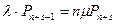
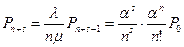
m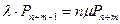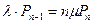

Дата добавления: 2014-01-07