Тема 6. Специальные модели исследования операций транспортного типа

Методы их решения: нахождение опорного решения транспортной задачи

Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из т пунктов отправления А₁, А₂,..., А_т в n пунктов назначения В₁, В₂,..., В_п. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через С_ij тарифы перевозки единицы груза из i -го пункта отправления в j - й пункт назначения, через a_i — запасы груза в i - м пункте отправления, через bj — потребности в грузе в j - м пункте назначения, а через X_ij — количество единиц груза, перевозимого из i - го пункта отправления в j - й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции

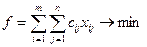(2.16)

при условиях

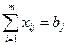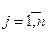() (2.17)

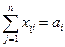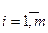() (2.18)

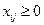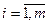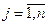(;) (2.19)

Поскольку переменные x_ij ( 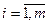; 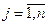) удовлетворяют системам линейных уравнений (2.17) и (2.18) и условию неотрицательности (2.19), обеспечивается доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.

Всякое неотрицательное решение систем линейных уравнений (2.17) и (2.18), определяемое матрицей X = (x_ij) ( 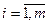; 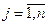), называется планом транспортной задачи.

Будем называть любой план перевозок допустимым, если он удовлетворяет условиям (2.17), (2.18), т. е. все заявки удовлетворены, все запасы исчерпаны).

План X^*= (x_ij) ( 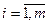; 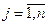), при котором функция (2.16) принимает свое минимальное значение, называется оптимальным планом транс портной задачи.

Обычно исходные данные транспортной задачи записывают в виде таблицы (табл. 2.12).

Таблица 2.12

Пункты отправления	Пункты назначения	Запасы
В1		Вj		Вп
А1	Х11	С11			Х1j	С1j			Х1n	С1n	a1
...	...										...
Аi	Хi1	Сi1			Хij	Сij			Хin	Сin	ai
...	...										...
Аm	Хm1	Сm1			Хmj	Сmj			Хmn	Сmn	am
Потребности	b1	...	bj	...	bn

Очевидно, общее наличие груза у поставщиков равно, а общая

потребность в грузе в пунктах назначения равна 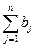единиц.

Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е.

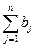= (2.20)

то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.

Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. чтобы выполнялось равенство (2.20).

Число переменных х_ij в транспортной задаче с т пунктами отправления и п пунктами назначения равно пт, а число уравнений в системах (2.17) и (2.18) равно n+m. Так как мы предполагаем, что выполняется условие (2.20), то число линейно независимых уравнений равно n+m-1.

Допустимый план будем называть опорным, если в нем отличны от нуля не более т+п-1 базисных перевозок, а остальные перевозки равны нулю.

Если в опорном плане число отличных от нуля компонент равно в точности n+m-1, то план является невырожденным, а если меньше — вырожденным.

Для определения опорного допустимого плана существует несколько методов например, метод северо-западного угла и метод минимального элемента.

Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи будет опорным и допустимым планом.

Ввиду исключительной практической важности транспортной задачи и специфики ее ограничений (каждая неизвестная входит лишь в два уравнения систем (2.17) и (2.18) и коэффициенты при неизвестных равны единице) для определения оптимального плана транспортной задачи разработаны специальные методы. Один из них — метод потенциалов.

Дата добавления: 2014-01-07