Тема 3. Обратная матрица. Матричный способ решения СЛАУ

Для самостоятельного решения.

1. 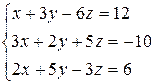; Ответ: x = 0; y = 0; z = -2.

Повторение. Матрицы и действия с ними. Понятие совмкстных систем.

Определим операцию деления матриц как операцию, обратную умножению.

Определение 3.1. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,

где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А^-1.

Теорема. Для того чтобы матрица А имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Т.е. каждая квадратная невырожденная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну. Рассмотрим общий подход к нахождению обратной матрицы. Исходя из определения произведения матриц, можно записать:

AX = E Þ 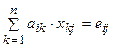, i=(1,n), j=(1,n),

e_ij = 0, i ¹ j,

e_ij = 1, i = j.

Таким образом, получаем систему уравнений:

,

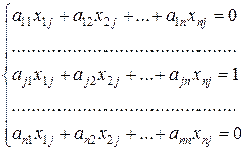Решив эту систему, находим элементы матрицы Х. Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:

,

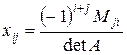где М_ji - дополнительный минор элемента а_ji матрицы А.

Обратная матрица также может быть найдена по формул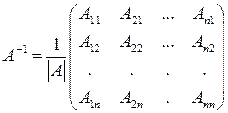е: , где 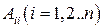- алгебраические дополнения матрицы А.

Пример 3.1. Дана матрица А = 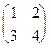, найти А^-1.

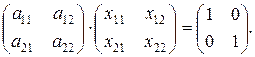
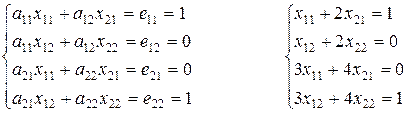
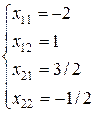
Таким образом, А^-1=.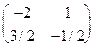

Пример 3.2. Дана матрица А = 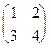, найти А^-1.

det A = 4 - 6 = -2.

M₁₁=4; M₁₂= 3; M₂₁= 2; M₂₂=1

x₁₁= -2; x₁₂= 1; x₂₁= 3/2; x₂₂= -1/2

Таким образом, А^-1=.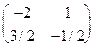

Cвойства обратных матриц

Самостоятельно проверить их справедливость.

1. ;

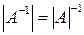2. ;

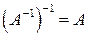3. ;

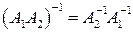4. .

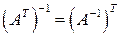Дата добавления: 2014-01-07