Тема 1. Основные понятия векторной алгебры

Все величины делятся на: скалярные (задаются числом), векторные (задаются и числом и направлением), тензорные (задаются квадратной матрицей).

Определение 1.1. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.

Определение 1.2. Длиной (модулем) вектора называется расстояние между началом и концом вектора.

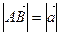
Определение 1.3. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.

Определение 1.4. Векторы называются компланарными, если существует плоскость, которой они параллельны.

Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.

Определение 1.5. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.

Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.

Определение 1.6. Единичным вектором (ортом) называется вектор, длина которого равна 1, а направление совпадает с самим вектором.

Определение 1.7. Линейными операциями над векторами называется сложение и умножение на число.

Суммой векторов является вектор - .

Произведение - 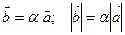, при этом коллинеарен .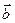

Вектор сонаправлен с вектором 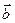(­­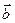), если a > 0.

Вектор противоположно направлен с вектором 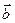(­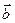¯), если a < 0.

Свойства векторов

1) + 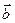= 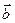+ - коммутативность.

2) + (+ ) = (+ )+ .

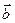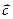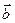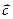3) + = .

4) +(-1) = .

5) (a×b)= a(b) – ассоциативность.

6) (a+b)= a+ b- дистрибутивность.

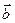7) a(+ ) = a+ a.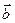

8) 1×= .

Определение 1.8.

1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.

2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.

3) Базисом на прямой называется любой ненулевой вектор.

Определение 1.9. Если 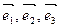- базис в пространстве и , то числа a, b и g - называются компонентами или координатами вектора в этом базисе.

В связи с этим можно записать следующие свойства:

- равные векторы имеют одинаковые координаты;

- при умножении вектора на число его компоненты тоже умножаются на это число,

= .

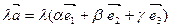- при сложении векторов складываются их соответствующие компоненты.

; ;

+ = .

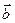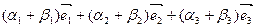Дата добавления: 2014-01-07