Модели описывающие процесс функционирования системы

В теории управления и в ТАУ, в частности, наиболее важным является понятие модели – определенной математической абстракции, характеризующей реальные процессы любой природы – физической, биологической, экономической и др.

Свойства любой системы проявляются в процессе ее функционирования. Для определения этих свойств следует подать на входы системы некоторые возмущающие воздействия и проанализировать выходы. Однако почти всегда проведение таких экспериментов с реальной системой экономически невыгодно, в связи с этим эксперименты для изучения свойств системы проводят не с реальными системами, а их моделями.

Моделирование – процесс проведения экспериментов на модели вместо прямых экспериментов на самой системе.

Модель - это процесс, выраженный через связи между переменными входа, выхода и переменными состояния, т.е. через уравнения системы.

Модель - это некоторая другая система, сохраняющая существенные черты оригинала и допускающая исследование физическими и математическими методами.

Для получения математического описания системы составляют описание отдельных ее элементов. В частности, для получения уравнений системы составляют уравнения для каждого входящего в нее элемента.

Совокупность всех уравнений элементов и дает уравнения системы.

Уравнения автоматической системы управления называют ее математической моделью.

[Источник – Теория автоматического управления. Учебник для вузов. В 2-х ч. Ч1 Теория линейных систем автоматического управления./ Бабаков Н.А., Воронов А.А., Воронова А.А. и др.; Под ред. А.А. Воронова. – 2-е издание перераб. и доп. – М.: Высшая школа, 1986г. - 367 стр. Ч2 Теория нелинейных и специальных систем автоматического управления./ Воронов А.А., Ким Д.П., Лохин В.М. и др.; Под ред. А.А. Воронова. – 2-е издание перераб. и доп. – М.: Высшая школа, 1986г.-504 стр.]

Следует отдавать себе отчет, что никакая математическая модель физической системы не является точной.

Мы можем повышать точность модели, увеличивая количество и сложность уравнений, но все равно никогда не достигнем абсолютной точности. Мы стремимся к тому, чтобы модель адекватно отражала поведение физической системы и в то же время не была слишком сложной.

Установлено, что разработка моделей физических систем занимает 80-90 процентов усилий необходимых для анализа и синтеза систем управления.

[Источник – Филипс Ч., Харбор Р. Системы управления с обратной связью. - М.: Лаборатория Базовых Знаний, 2001г. 616 стр.]

Классификация систем:

Системы разделяют на классы по различным признакам, и в зависимости от решаемой задачи можно выбирать разные принципы классификации.

Классификации всегда относительны. Так в детерминированной системе можно найти элементы стохастичности, и, напротив, детерминированную систему можно считать частным случаем стохастической (при вероятности равной единице).

Цель любой классификации – ограничить выбор подходов к отображению системы, дать рекомендации по выбору методов моделирования и исследования для соответствующего класса систем. При этом система может быть одновременно охарактеризована несколькими признаками, т.е. ей может быть найдено место в разных классификациях, каждая из которых может оказаться полезной при выборе методов моделирования.

Системы подразделяют на:

· Статические – состояние которых не зависит от времени.

· Динамические – состояние которых зависит от времени.

Статические системы можно описывать уравнениями вход-выход: Y=F(X)

Динамические системы описываются уравнениями вход – состояние – выход: Y(t)=F(Z(t), X(t))

· Непрерывные - интервал функционирования представляет собой отрезок оси.

· Дискретные - интервал функционирования представляет собой совокупность дискретных моментов времени.

· Детерминированные – системы, при описании которых не учитываются случайные факторы.

· Стохастические - системы, при описании которых учитываются случайные факторы.

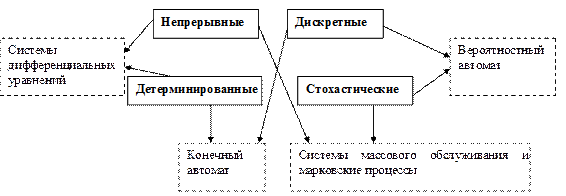
Математические модели детерминированных систем функционирующих в дискретные моменты времени являются различные схемы конечных автоматов.

Конечный автомат функционирует в дискретные моменты времени: t₀, t₁, t₂, …

Dt=t_i+1 - t_i

Если за единицу времени взять Dt, то можно сказать что конечный автомат принимает значения: 0, 1, 2, …

Для конечного автомата множество состояний системы и множества входных и входных воздействий являются конечными.

Z={Z₁, Z₂, … Z_n }

X={X₁, X₂, … X_n}

Y={Y₁, Y₂, … Y_n}

Конечный автомат функционирует следующим образом:

- В момент времени t поступает входное воздействие X(t), которое переводит автомат в новое состояние в соответствии с функцией перехода: Z(t+1)=F(Z(t), X(t))

- При этом выходное воздействие определяется по формуле выхода: Y(t)=F(Z(t), X(t))

Детерминированные системы, функционирующие в непрерывном времени описываются с помощью дифференциальных уравнений.

Стохастические системы, функционирующие в дискретные моменты времени описываются с помощью вероятностных автоматов. (Балагин стр. 204)

Стохастические системы с непрерывным временем описываются с помощью математического аппарата, систем массового обслуживания и марковских процессов. (Балагин стр. 205)

Пример задания конечного автомата.

Абстрактный автоматА задается как совокупность:

1. конечного множества X входных сигналов – называемого входным алфавитом;

2. конечного множества Y выходных сигналов – называемого выходным алфавитом;

3. произвольного конечного множества Z состояний автомата;

4. начальное состояние автомата Z(0)=Z₀, в начальный момент времени t=0 автомат всегда находится в своем начальном состоянии Z₀;

5. функция переходов автомата;

6. функция выходов автомата;

Чтобы задать конечный автомат, необходимо описать входной и выходной алфавиты, задать начальное состояние автомата и множество его промежуточных состояний, а так же записать функции его переходов и выходов.

Простейший табличный способ задания конечного автомата основан на использовании таблиц переходов и выходов.

Строки обеих этих таблиц обозначаются входными сигналами автомата, а столбцы – его состояниями. На пересечении строки и столбца таблицы переходов ставится соответствующее значение функции переходов, а в таблице выходов – соответствующее значение функции выходов.

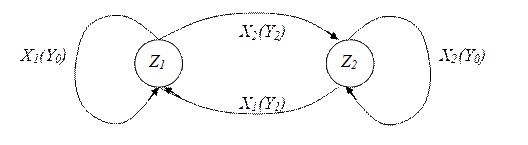
Второй способ задания автоматов основан на использовании направленных графов.

Вершины графа отождествляются с состояниями автомата, а стрелки с выходными сигналами. Если входной сигнал вызывает переход автомата из одного состояния в другое то на графе этому сигналу соответствует стрелка соединяющая соответствующие вершины.

Переход от задания конечного автомата с помощью таблиц к заданию с помощью графа и обратный переход выполняются вполне очевидным образом.

Рассмотрим пример - станка автомата.

Если в такт работы t поступает заготовка, то в следующем такте она обрабатывается.

Если в такт работы t заготовка не поступает, то в следующем такте автомат отключается.

Опишем работу станка с помощью конечного автомата.

X₁ – заготовка поступила;

X₂ – заготовка не поступила.

X={X₁, X₂}

Z₁ – состояние обработки заготовки станком;

Z₂ – состояние простоя станка.

Z={Z₁, Z₂}

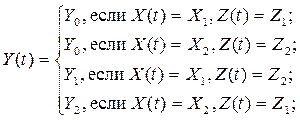
Y₀ – станок остается в прежнем состоянии;

Y₁ – станок включается;

Y₂ – станок выключается.

Y={Y₀, Y₁, Y₂}

Таблица переходов Таблица выходов

Z	Z1	Z2
X1	Z1	Z1
X2	Z2	Z2

Y	Z1	Z2
X1	Y0	Y1
X2	Y2	Y0

Построим граф состояний

Дата добавления: 2014-01-07