Класификация динамических звеньев второго порядка

Дифференциальные уравнения таких звеньев имеют общий вид

,

а передаточная функция – W(p) = K / (T₂² p² + T₁ p + 1).

В зависимости от соотношения постоянных времени Т₁ и Т₂:

а) Если 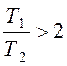, то звено называется апериодическим второго порядка. Переходной процесс представляет собой S-образную кривую с перегибом в точке О (рис. 6.10).

Примеры апериодического звена второго порядка (рис. 6.11):

а) последовательное соединение двух пневматических емкостей, если входная величина х = Рпит, а выходная величина – давление во второй емкости у = Р;

б) двойная электрическая RC –цепочка.

Рис. 6.10. Переходная характеристика апериодического звена

второго порядка

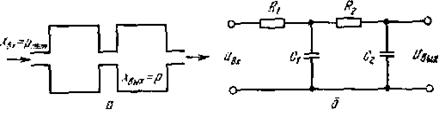Рис. 6.11. Примеры апериодических звеньев второго порядка

б) Если , то звено называется колебательным.

Дифференциальное уравнение звена обычно представляется в виде

,

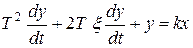где x – коэффициент затухания, 0 < x < 1. При этом корни характеристического уравнения комплексные.

Переходная характеристика звена представляет собой периодический сходящийся процесс (рис. 6.12), описываемый формулой

,

где a = x / T, .

Примерами колебательных звеньев могут служить (рис. 6.13):

а) электрический колебательный RCL– контур (R – активное сопротивление, C – емкость, L – индуктивность);

б) упругая механическая передача, которая состоит из входного 1 и выходного 2 валов, упругого элемента 3, маховика 4 и демпфера 5, оказывающего сопротивление вращению вала. Входная величина х – угол поворота входного вала j₁, выходная величина у – угол поворота выходного вала j₂.

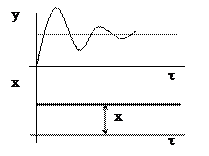Рис. 6.12. Переходная характеристика колебательного звена

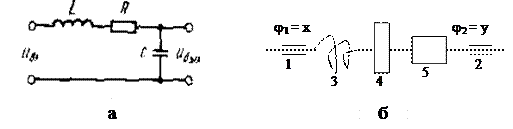Рис. 6.13. Примеры колебательных звеньев

в) Если Т₁ = 0, то есть нет демпфирования, имеем консервативное звено –

.

Переходная характеристика представляет собой гармонические незатухающие колебания (в природе такого звена нет).

г) Если Т₁ < 0 – это неустойчивое колебательное звено с расходящимися колебаниями.

К динамическим звеньям второго порядка относятся также рассмотренные выше реальные интегрирующее и дифференцирующее звенья.

Классификацию динамических звеньев второго порядка можно графически изобразить таким образом (рис. 6.14).

Рис. 6.14. Классификация динамических звеньев второго порядка

Дата добавления: 2014-01-07