Первый опорный план

ТРАНСПОРТНАЯ ЗАДАЧА (МЕТОД ПОТЕНЦИАЛОВ)

Анализ основных экономических показателей

№	Показатели	Ячмень	Карто- фель	Сахарная свекла	Капуста	Итого
	Посевная площадь, га	1 270,479	7,018	3,933	549,184	1830,614
	Посевная площадь, %	69,40	0,38	0,21	30,00	100,00
	Валовой сбор, т	2 413,911	66,667	70,0	15 377,154
	В т. ч. на семена, т	72,417	—	—	—	72,417
	страховой фонд, т	144,835	16,67	—	—
	на элеватор, т	362,087	—	—	—	362,087
	в магазин, т	—	50,00	—	—	50,00
	на переработку, т	—	—	70,00	—	70,00
	в овощехранилище, т	—	—	—	65,00	65,00
	на собствен.нужды, т	—	—	—	4 613,146	4 613,146
	на рынок, т	1 834,572	—	—	10 699,008
	Потр..удобр. N, т	21,5981	0,2175	0,0944	4,9427	26,8527
	Потр..удобр. P, т	33,0325	0,1614	0,1730	11,5329	44,8998
	Потр..удобр. K, т	41,9258	0,1825	0,2202	9,3361	51,6646
	Затраты тыс. чел/ час	2,0328	0,60	1,10	83,90	110,00
	Товарная прод. тыс.руб.	803,832	27,0	28,0	25 859,619	26 718,451
	Затраты, тыс. руб.	5 215,318	36,246	27,054	2 375,224	7 653,841
	в т.ч. N тыс. руб.	755,93	7,61	3,3	172,99	939,846
	P тыс. руб.	1 981,95	9,68	10,38	691,97	2 693,98
	K тыс. руб.	2 096,29	9,13	11,01	466,81	2 583,24
	Убыток тыс. руб.	4411,478	9,25	—	—	4420,728
	Прибыль, тыс. руб.	—	—	0,95	23 484,395	23 485,349
	Экономический эффект производства с.-х. продукции, тыс. руб.	19 064,61

Важным частным случаем задачи линейного программирования является транспортная задача. Суть данной задачи, найти объемы перевозок для каждой пары «поставщик – потребитель» так, чтобы:

– мощности всех поставщиков были реализованы;

– спросы всех потребителей были удовлетворены;

– суммарные затраты на перевозку были бы минимальны.

Задача № 1.4.1.

Двум предприятиям требуется сырье в количестве b ₁ и b ₂ тонн. Запасы сосредоточены в трех пунктах в количестве a ₁, a ₂, и a ₃ тонн. Известна матрица С расстояний (км). x_ij – количество сырья, которое планируется завести j -му предприятию с i- го пункта хранения.

Требуется:

–найти x ₁₁, x ₁₂ ,...,x ₃₂ методом потенциалов так, чтобы при перевозке сырья общее количество тонно-километр было минимальным;

– проверить правильность решения симплекс-методом (программный комплекс «Блок-3»). Исходная информация:

	а 1= 4; а 2 = 5; а 3 = 6.
	b 1= 2; b 2= 8;
	C =

Для решения данной задачи методом потенциалов необходимо выполнение условий (закрытая задача):

å a_i = å b_j.

В нашем случае å a_i = 15, а å b_j = 10. Таким образом, сумма по а_i больше суммы b_j на 5 (открытая задача). Для равенства условия, необходимо вести фиктивное предприятие b ₃= 5. Элементы столбца затрат матрицы С для b ₃ равны 0. Исходные данные записываются в таблицу (табл. 11):

Таблица 11

Исходная таблица

				å ai
å bj

В угловых, малых клетках табл. 11 стоят элементы матрицы С. Для определения потенциалов Х и Y необходимо найти любое решение (допустимое решение – опорный план). В нашем случае его целесообразно найти методом северо-западного угла. После выполнения ряда операций первый опорный план примет вид табл. 12.

Таблица 12

				å ai
å bj

Значение целевой функции равно:

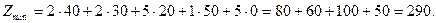
В дальнейшем, при нахождении нового решения, необходимо рассчитывать значение функционала для сравнения с предыдущим, чтобы оценить правильность решения. Для проверки на оптимальность данного решения, воспользуемся методом потенциалов. Процесс решения задачи методом потенциалов целесообразно разбить на шаги.

1-й шаг. Рассчитаем потенциалы Х и Y для занятых клеток по следующему правилу: С_ij = X_i + Y_j или в упрощенном виде С = X + Y, причем в начале необходимо присвоить значение 0 потенциалу X или Y. В нашем случае, например Y ₁ = 0.

Вычислим все значения потенциалов: Y ₁= 0;

X ₁ = C – Y ₁ = 40 – 0 = 40; Y ₂ = C – X ₁ = 30 – 40 = –10;

X ₂ = C – Y ₂ = 20 – (–10) = 30; X ₃ = C – Y ₂ = 50 – (–10) = 60;

Y ₃ = C – X ₃ = 0 – 60 = –60.

Отобразим проведенные расчеты в табл. 30.

2-й шаг. Рассчитаем коэффициенты g _ij по следующему правилу для незанятых клеток g _ij = С_ij – (X_i + Y_j) или в упрощенном виде g = С – (X + Y).

Если все g ³ 0, то найденное решение является оптимальное и на этом заканчивается решение 1-й части задачи.

Таблица 13

Первый опорный план – проверка на оптимальность

У Х		–10	–60	å ai
å bj

g₁₃ = 0 – (–60 + 40) = 20; g₂₁ = 10 – (0 + 30) = –20;

g₂₃ = 0 – (–60 + 30) = 30; g₃₁ = 5 – (0 + 60) = –55;

В нашем примере есть отрицательные значения g и это значит, что найденное решение не является оптимальным и его необходимо улучшить. Для этого необходимо выбрать максимальное число g со знаком «минус». В нашем случае g₃₁ = –55.

В клетку с координатами 3-я строка и 1-й столбец поставим знак + и построим цикл по занятым клеткам. Начала цикла берется из клетки со знаком +. Цикл представляет собой плоский многоугольник с вершинами 90° и может иметь следующий вид:

После построения цикла таблица примет следующий вид (табл.14):

Таблица 14

Первый опорный план – построение цикла

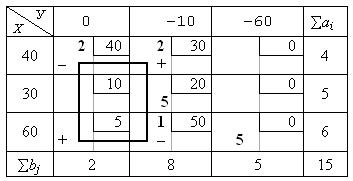
3-й шаг. Последовательно по вершинам цикла, проставим знаки + и –начиная с клетки +. В клетках со знаком минус выбрать числа (количество грузов) и сравнить их между собой. Необходимо из них выбрать наименьшее. В нашем случае в клетках со знаком минус стоят следующие числа: 2 и 1. Наименьшее из этих чисел – число 1. Обозначим его D = 1. Теперь необходимо переместить по циклу это количество груза. В клетках со знаком + добавить число 1, а в клетках со знаком – вычесть число 1. В результате расчетов, получим новую табл. 15.

Таблица 15

Дата добавления: 2014-01-07