Дискретный случайный процесс с дискретным временем

Определение 9. Случайный процесс, протекающий в системе, называется процессом с дискретным временем, если переходы системы из одного состояния в состояние могут осуществляться только в заранее определенные моменты времени t ₁, t ₂, ×××, называемые шагами или этапами этого процесса.

Определение 10. Случайный процесс, протекающий в системе, называется процессом с непрерывным временем, если ее переходы из состояния в состояние возможны в любые, заранее неизвестные, случайные моменты времени.

Определение 11. Случайная последовательность называется марковской цепью, если для каждого шага вероятность перехода из любого состояния s_i в любое состояние s_j не зависит от того, когда и как система s оказалась в состоянии s_i.

Обозначим через 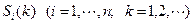событие, состоящее в том, что с k -го до (k +1)-го шага система S находится в состоянии s_i, т.е. S_i (k) есть событие S (t)= s_i при t Î[ t_k, t_{k +1}). Так как система S в любой момент t может пребывать только в одном из своих возможных состояний s ₁, s ₂,×××, s_n, то при каждом k =1,2, ×××, события S ₁(k), S ₂(k), ×××, S_n (k) несовместны и образуют полную группу.

Основными характеристиками марковских цепей являются вероятности событий S_i (k).

Определение 12. Вероятности 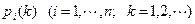называются вероятностями состояний.

Определение 13. Переходной вероятностью p_ij (k) k -го шага называется вероятность непосредственного перехода системы S в момент t_k из состояния s_i в состояние s_j.

Определение 14. Если ни одна из переходных вероятностей 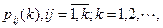не зависит от шага k (в этом случае их обозначают p_ij), то марковская цепь называется однородная; в противном случае марковская цепь называется необнородной.

Теорема 6.1. Для однородной марковской цепи вектор-строка вероятностей состояний от k -го до (k +1)-го шага равна произведению вектор-строка вероятностей состояний от (k –1) до k -го шага на матрицу переходных вероятностей:

Задача № 5.2.

Цена реализованной молочной продукции на рынке меняется в течении года (постоянна 4 месяца) на 4 %, –1 % и 6 %.

Определить вероятности колебаний цен на рынке на молочную продукцию в конце года, если в конце года она составлила 6%, причем размеченный граф состояний представлен ниже:

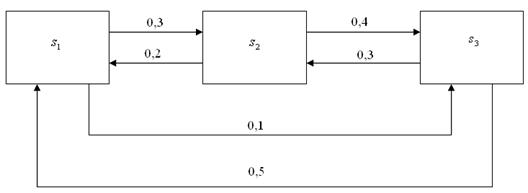
Рис. 26. Граф состояний вероятностей колебаний цен на рынке

Решение: Будем считать, что в данной системе протекает однородный марковский дискретный случайный процесс с дискретным временем, т.е. имеет место однородная марковская цепь. Подсчитаем недостающие 3 вероятности, исходя из условия полной группы вероятностей:

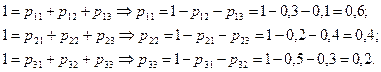
Составим матрицу переходных вероятностей:

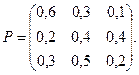
В начальный момент колебания на цен на рынке составляло 6 %, то можно считать, что в начальный момент t =0 система находилась в состоянии s ₃. Поэтому начальное распределение вероятностей имеет следующий вид:

Вероятность колебания цен на рынке по истечения года составит n =3 и k =3. Предварительно, необходимо найти P ³:

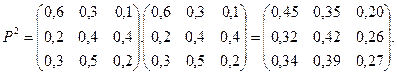
Окончательно получаем:

Таким образом, вероятности колебаний цен 4% –1 % и 6 % равны соответственно 0,363; 0,393; 0,244. Вероятнее всего к концу года цена на молочную продукцию в среднем снизится на 1%.

Фрагмент выполнения умножения матриц в «Блокнот-4» приведен рис. 27.

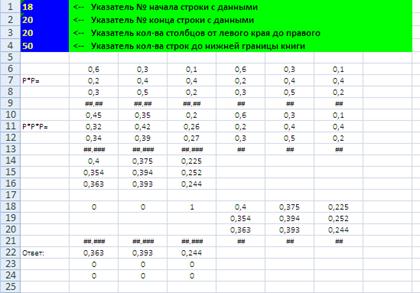
Рис. 27.Фрагмент выполнения задачи № 6.2

Дата добавления: 2014-01-07