
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предел последовательности
|
|
|
|
Рассмотрим последовательность 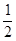 ,
, 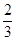 ,
, 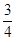 ,.... Её можно рассматривать как переменную величину
,.... Её можно рассматривать как переменную величину  =
= 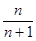 ,
,
n = 1,2,3,..., функцию натурального аргумента  =
= 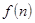 . Значение данной переменной величины
. Значение данной переменной величины  отличается от единицы на 0,1 при n = 9, на 0,01 при n = 99, на 0,001 при
отличается от единицы на 0,1 при n = 9, на 0,01 при n = 99, на 0,001 при
n = 999 и т.д. Очевидно, что эта переменная величина может как угодно близко приблизиться к единице. Говорят, что единица является её пределом.
Определение 1. Число 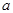 называется пределом числовой последовательности
называется пределом числовой последовательности 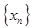 , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа  > 0 существует такой номер
> 0 существует такой номер 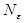 , что все значения
, что все значения  при n >
при n > 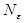 удовлетворяют неравенству
удовлетворяют неравенству 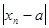 <
<  .
.
Пишут 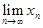 =
= 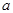 .
.
Геометрически это означает, что для любой O (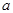 ,
, ) найдётся такой номер
) найдётся такой номер 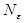 , что все
, что все  при n >
при n > 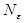 будут принадлежать этой
будут принадлежать этой  –окрестности. ("
–окрестности. (" > 0 $
> 0 $ 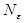 (n >
(n > 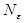 Þ
Þ  Î O (
Î O (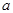 ,
, ))).
))).
Если  = C = const, то
= C = const, то 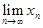 = C, т.к.
= C, т.к. 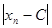 = 0 <
= 0 <  для любых n.
для любых n.
Чтобы найти предел последовательности, используя только его определение, следует поступить так:
1) предположить, что предел равен 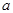 ;
;
2) решить неравенство 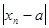 <
<  относительно n для любого
относительно n для любого  > 0;
> 0;
3) если решение неравенства имеет вид n > 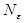 , то предположение, что предел равен
, то предположение, что предел равен 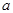 , верно и предел найден.
, верно и предел найден.
Пример1. Найти предел последовательности  =
= 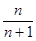 .
.
Решение. 1) Предположим, что 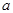 = 1.
= 1.
2) Решим неравенство  <
<  ,
,
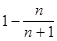 <
<  ,
, 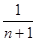 <
<  ,
,
n + 1 > 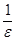 , n >
, n > 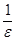 – 1 =
– 1 = 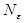 .
.
3) Итак, для всех n >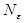 неравенство
неравенство
 <
< выполняется, поэтому
выполняется, поэтому 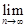
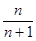 =1 согласно определению предела.
=1 согласно определению предела.
Замечание. Число 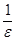 – 1 не для всех
– 1 не для всех  является натуральным, поэтому за
является натуральным, поэтому за 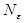 следует взять целую часть этого числа, т.е.
следует взять целую часть этого числа, т.е. 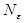 = Е (
= Е (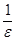 – 1).
– 1).
Теорема 1. Если последовательность имеет предел, то он единственный.
Доказательство (от противного). Пусть предел не единственный. Выберем два предела 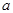 =
= 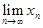 и
и 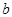 = =
= =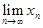 ,
,
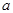 <
< 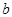 . Выберем O (
. Выберем O (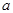 ,
, ) и O (
) и O (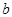 ,
, ) так, чтобы они не имели общих точек. Для этого достаточно взять
) так, чтобы они не имели общих точек. Для этого достаточно взять  <
< 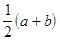 . По определению предела $
. По определению предела $ 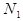 " n >
" n > 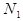 (
( Î O (
Î O (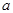 ,
, )) и $
)) и $ 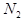 " n >
" n > 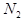 (
( Î O(
Î O(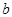 ,
, )). Пусть
)). Пусть 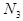 = max (
= max (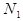 ,
,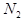 ), тогда " n >
), тогда " n > 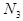 (
( ÎO (
ÎO (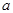 ,
, ) ^
) ^  Î O(
Î O(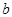 ,
, )), что не возможно, т.к. окрестности не пересекаются. (^ - символ конъюнкции). Полученное противоречие доказывает теорему.
)), что не возможно, т.к. окрестности не пересекаются. (^ - символ конъюнкции). Полученное противоречие доказывает теорему.
Определение 2. Последовательность 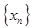 называется бесконечно большой (пишут
называется бесконечно большой (пишут 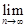
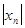 = ¥), если для любого значения М > 0 найдётся такой номер
= ¥), если для любого значения М > 0 найдётся такой номер 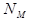 , что все значения
, что все значения  при n >
при n > 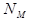 удовлетворяют неравенству
удовлетворяют неравенству 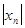 > M.
> M.
Например, последовательности  = n,
= n,  = – n,
= – n, 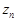 =
=
= 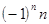 являются бесконечно большими.
являются бесконечно большими.
Замечание. Следует различать неограниченную и бесконечно большую последовательности. Например, последовательность 1, 0,3,0,5,0,... является неограниченной сверху, но она не является бесконечно большой.
Если последовательность имеет конечный предел, то она называется сходящейся. В противном случае – расходящейся. Последовательность 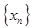 называется неубывающей, если
называется неубывающей, если  £
£ 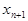 для любого n. Если
для любого n. Если  ³
³ 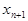 , – то это невозрастающая последовательность. Невозрастающая и неубывающая последовательности называются монотонными. Если неравенства строгие (
, – то это невозрастающая последовательность. Невозрастающая и неубывающая последовательности называются монотонными. Если неравенства строгие ( <
< 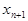 ,
,  >
> 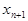 ), то последовательности называются строго монотонными.
), то последовательности называются строго монотонными.
Теорема 2. Монотонная ограниченная последовательность сходится.
Доказательство. Пусть последовательность неубывающая, т.е.  £
£ 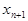 . Согласно теореме 3 §1 последовательность
. Согласно теореме 3 §1 последовательность 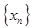 имеет точную верхнюю грань sup
имеет точную верхнюю грань sup = M. По определению точной верхней грани
= M. По определению точной верхней грани  £ M для любого n и M –
£ M для любого n и M – 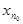 <
<  , где
, где 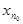 – некоторый член последовательности. Поскольку последовательность неубывающая, то последнее неравенство будет выполняться для всех n ³ n0, т.е.
– некоторый член последовательности. Поскольку последовательность неубывающая, то последнее неравенство будет выполняться для всех n ³ n0, т.е. 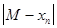 <
<  " n > n0. А это означает, что M =
" n > n0. А это означает, что M = 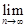
 . Доказательство аналогично для невозрастающей последовательности. Теорема доказана.
. Доказательство аналогично для невозрастающей последовательности. Теорема доказана.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 291; Нарушение авторских прав?; Мы поможем в написании вашей работы!