Теоремы умножения и разложения

Сверткой двух функций 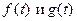(обозначают 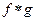) называют интеграл Покажем, что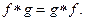

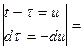
Действительно,Свойство доказано.

Отметим без доказательства, что свертка двух оригиналов является оригиналом.

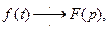
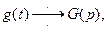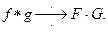Теорема 1 (Борель). Если то (1)

Доказательство.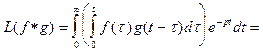

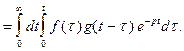
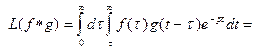
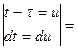
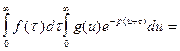
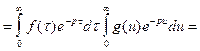
Рассматривая этот интеграл как двойной по области, изображенной на рисунке 3, поменяем порядок интегрирования. Получим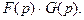Теорема доказана.

Формула (1) носит название теоремы умножения. Итак,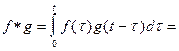 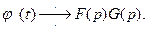(1')

Поскольку то воспользовавшись свойством дифференцирования оригинала, из 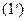получим

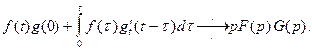(2)

Формулу (2) называют формулой Дюамеля. В силу симметрии свертки формулу (2) можно переписать иначе

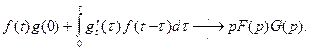(2')

Пример 1. Переходная функция 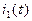электрической цепи известна (см. пример 6 §2). Найти ток в этой цепи при нулевых начальных условиях и произвольной э.д.с.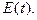

Решение. Запишем операторный закон Ома 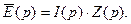(3)

Подставляя в (3) 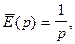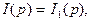где 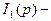изображение переходной функции 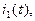найдем операторное сопротивление 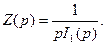Зная его, найдем из (3) изображение тока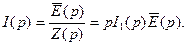

По формуле Дюамеля (2') найдем искомый ток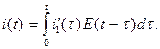

Теорема 2 (первая теорема разложения). Если функция разлагается в окрестности бесконечно удаленной точки в ряд Лорана 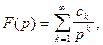то она является изображением оригинала

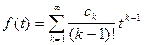(4)

(без доказательства).

Пример 2. Найти оригинал изображения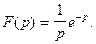

Решение. Разложим функцию в ряд Лорана в окрестности бесконечно удаленной точки.

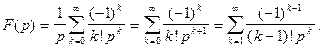
Согласно теореме 2

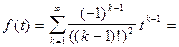
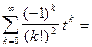
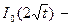функция Бесселя.

Если изображение 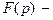дробно рациональная функция 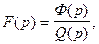то эта дробь правильная (см. следствие из теоремы 3 §1). Особыми точками дробно рациональной функции являются только изолированные полюсы, поэтому она удовлетворяет лемме Жордана. Отсюда ясно, что несобственный интеграл в формуле обращения можно вычислить с помощью вычетов, т.е. оригинал определяется формулой

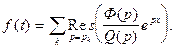(4)

Здесь 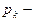нули знаменателя 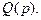Формулу (4) называют второй теоремой разложения. Она упрощается, если все нули знаменателя простые. В этом случае 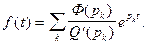(5)

Пример 3. По изображению 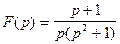найти оригинал.

Решение. Корни знаменателя 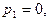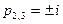простые, поэтому воспользуемся (5). Получим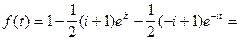

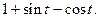
Дата добавления: 2014-01-07