Решение. Переходной функцией называется отклик электрической цепи на единичное воздействие при нулевых начальных условиях

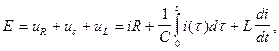(1)

где i(t) - ток.

Переходной функцией называется отклик электрической цепи на единичное воздействие при нулевых начальных условиях. В нашем случае это решение уравнения (1) при 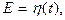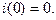Пусть 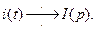Найдем изображение уравнения (1).

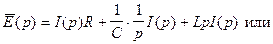
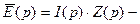операторный закон Ома,

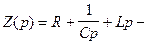операторное сопротивление (импеданс цепи).

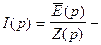изображение тока. Чтобы найти ток (оригинал), воспользуемся теоремой обращения

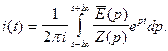(2)

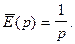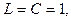
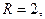В нашем случае Пусть тогда 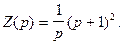Подставляя все это в (2), получим переходную функцию

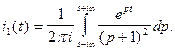(3)

Согласно теореме 3 §1 изображение является аналитической функцией в правой полуплоскости. Поэтому в интеграле (3) выберем таким, чтобы все особые точки подынтегральной функции были левее прямой 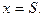Используя лемму 3 и основную теорему о вычетах (см. §7, гл.1), вычислим интеграл (3)

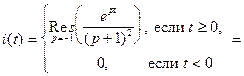
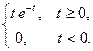
7. Интегрирование изображения. Есл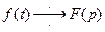ии 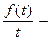оригинал, то 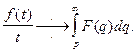Действительно, пусть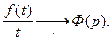

Тогда по свойству 4 получим 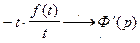или 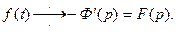Интегрируя последнее равенство, найдем 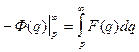или 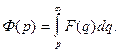Свойство доказано.

Пример 7. Найти изображение оригинала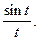

Решение. 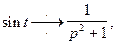тогда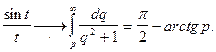

Пример 8. Найти изображение интегрального синуса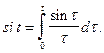

Решение. Используя свойство 6 и результат примера 7, найдем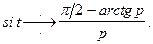

Дата добавления: 2014-01-07