Порядка. Задача Штурма-Лиувилля (краевая задача на собственные значения)

Задача Штурма-Лиувилля (краевая задача на собственные значения).

Оператором Штурма-Лиувилля называется дифференциальный оператор 2-го порядка , где коэффициенты .

Поставим вопрос: при каких значениях параметра λ существует нетривиальное решение

краевой задачи, где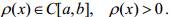

Такая задача называется краевой задачей на собственные значения и собственные функции для оператора Штурма-Лиувилля (сокращенно – задача Штурма-Лиувилля); числа, при которых существуют нетривиальные решения, называются собственными значениями, а соответствующие нетривиальные решения – собственными функциями.

Теорема (Стеклова). Любая функция, удовлетворяющая однородным краевым условиям, представима в виде абсолютно и равномерно сходящегося ряда Фурье по ортонормированной с весом ρ(x) системе собственных функций задачи Штурма-

Лиувилля (с теми же краевыми условиями) , где коэффициенты Фурье определяются формулой .

Графики решений y=y(x) скалярного ОДУ первого порядка, разрешенного относительно производной y′=f(x,y), называются его интегральными кривыми.

Таким образом, зная правую часть уравнения y′=f(x,y), можно заранее построить касательные ко всем интегральным кривым во всех точках: для этого каждой точке (x0,y0) нужно сопоставить проходящую через нее прямую с угловым коэффициентом k = f(x0,y0). Полученное соответствие между точками плоскости и проходящими через нее прямыми, называется полем

направлений уравнения y′=f(x,y).

Изоклины – кривые на (x,y)-плоскости, вдоль которых угловой коэффициент k сохраняет неизменное значение.

Определение 14 (см. также опр. 12). Если для любого решения ОДУ y=ϕ(x) существует функция 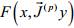такая, что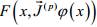=const при всех x, то такая функция называется первым интегралом ОДУ.

В физических задачах первыми интегралами могут быть энергия, импульс, момент

инерции, масса, заряд и т.д.

Выражение общего решения или полного интеграла через элементарные функции и интегралы от них (берущихся или не берущихся в элементарных функциях) называют интегрированием данного ОДУ в квадратурах.

1) Начальная задача (задача Коши):

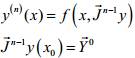- начальные условия .

2) Краевая задача (2-х точечная):

граничные условия первого рода (задача Дирихле):

граничные условия второго рода (задача Неймана):

граничные условия третьего рода:

периодические граничные условия: .

3) Периодическая задача. В общем случае задача о периодических решениях – это

задача о нахождении T -периодического решения уравнения с T -периодической по переменной t правой частью: .

Дата добавления: 2014-01-07