Принцип подвійності

Ґрати

ЛЕКЦІЯ 12

Розглянемо безліч на мал. 2-з. Для двох елементів x= { a }, y= { a, b } выполнятется відношення порядку: x £ y, тобто { a } Í { a, b }. Для цих двох елементів { a }= inf{x, y} є точною нижньою гранню, {a, b}= sup{x, y} є точною верхньою гранню. Елементи { a }, { b } непорівнянні. Однак для них існує елемент u = Æ, такий що u £ x і u £ y. Цей елемент – “найближчий нижній сусід” – і буде точною нижньою гранню елементів { a} і { b}: inf{ { a }, { b }} = Æ. Йому відповідає перетинання даних безлічей. Точною верхньою гранню цих двох елементів буде елемент v, такий, що x £ v і y £ v, і не існує такого z, щоб x £ z £ v і y £ z £ v. Цей елемент – “найближчий верхній сусід” – є безліч { a, b }= sup{x, y}, що є об'єднанням двох даних безлічей.

Побудуємо діаграму Хассе для множини-ступеня Ã(Р) = {Æ, { a }, { b }, { c }, { a, b }, { a, c }, { b, c }, { a, b, c }} (мал. 3). Тут точною нижньою гранню підмножин є їхнє теоретико-множинне перетинання, наприклад, для { a } і { b } це Æ, для { a, b } і { b, c } це { b } і т.д., а точною верхньою гранню двох підмножин є їхнє теоретико-множинне об'єднання, наприклад, для { a } і { b } це { a, b }, для { a, b } і { b, c } це { a, b, c } і т.д.

Дивлячись на діаграму Ã(P), можна зробити висновок, що в інтерпретації теорії множин операції sup (x, y) відповідає операція об'єднання, а inf (x, y) – операція перетинання безлічей. Ця аналогія послужила підставою для вибору найменування операції перебування точної верхньої грані – “об'єднання” (позначається Ú), і точної нижньої грані – “перетинання” (позначається Ù), у теорії ґрат (див. [1]).

Тепер ми можемо визначити, що таке ґрати.

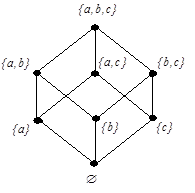Рис. 3.Діаграма Хассе Ã(P)

Ґратами називається упорядкована безліч, у якому будь-які два елементи x і y мають точну нижню грань, називану перетинанням, (позначається inf{x, y} º x Ù y), і точну верхню грань, називану об'єднанням (позначається sup{x, y} º x Ú y).

Безліч Ã(P) на мал. 3 утворить ґрати. Узагалі, безліч усіх підмножин деякої безлічі X утворить ґрати. Будь-який ланцюг також є ґратами, у якій x Ù y збігається з меншим, а x Ú y з великим з елементів x, y.

Відношення, зворотне для відношення порядку, саме є упорядкованістю. Дійсно, якщо x £ y ( “ x менше y “), те y ³ x ( “ y більше x “). Наприклад, якщо x £ y є відношення “ x Í y “, те зворотне йому відношення y ³ x є “ y Ê x “. Для будь-якого упорядкованої безлічі X безліч Y, обумовлене на тих же елементах відношенням, зворотним до упорядкованості в X, називається двоїстою безліччю. Наприклад, для множини-ступеня двоїстим йому безліччю буде безліч з відношенням порядку B Ê A – “B включає A”. Діаграма такої безлічі буде “переверненої”: нулем цієї безлічі буде безліч P={a, b, c}, а одиницею – Æ; операції sup{x, y} буде відповідати перетинання, а inf{x, y} – об'єднання підмножин.

Дата добавления: 2014-01-07