Словесна постановка завдання

На цьому етапі робиться опис об'єкту і детальніший опис предмету дослідження. Виділяються проблеми, пов'язані із структурою і складом системи. Формулюються актуальність, мета і завдання дослідження. Визначаються кордони дослідження, тобто граничні значення вхідних і вихідних характеристик системи.

Опис предмету дослідження – робиться спочатку словесним (вербальним), а потім графічним (блок-схемами). Словесний опис системи може бути складений в результаті грунтовного вивчення її процесу функціонування і елементів, що здійснюють його. Структура опису залежить від того, яке завдання дослідження системи необхідно вирішити. Якщо це завдання пряма, то перш за все описуються елементи системи, їх властивості і завдання, які вони можуть вирішувати відповідно до своїх властивостей. Потім описуються елементарні і складені або системні операції і їх цеи. Визначається сукупність і послідовність операцій, які можуть привести до головної мети функціонування системи.

Якщо завдання дослідження системи зворотне, то спочатку описується сукупність і послідовність операцій, які можуть привести до головної мети, а потім властивості елементів, які вони повинні мати для участі в цих операціях. При цьому використовується накопичений досвід і результати спостережень за процесами функціонування реальних аналогічних систем з врахуванням особливостей проектованої системи.

2) Вибір показника ефективності, математична постановка завдання

Передбачимо, що перший етап дослідження системи завершений. Визначені проблеми, кордони дослідження, мета і завдання функціонування системи. Тоді можна приступити до вибору показника ефективності функціонування, за значенням якого можна судити про те - досягає система мети чи ні, а якщо досягає, то наскільки.

Таким чином, показник ефективності має бути мірою досягнення мети.

Тому під показником ефективності функціонування складної системи – розуміється така її числова характеристика, яка оцінює міру пристосованості системи до досягнення поставленої перед нею мети.

У загальному випадку, виконання операцій, складових функціонування системи, супроводжується елементами випадковості, звідси факт досягнення мети, як правило, не може бути точно передбачений, тобто буде випадковим. Тому як показники ефективності приймаються невипадкові характеристики випадкової величини.

Для оцінки очікуваної ефективності діяльності деякого підприємства можуть бути прийнятий наступні два типи показників ефективності:

- Перший - вірогідність події, наприклад виконання замовлення в заданий час.

- Другий - математичне чекання (середнє значення), якщо метою є досягнення максимальної продуктивності. Для оцінки великих за об'ємом, складних по фізичному єству процесів виникає необхідність залучення декількох показників. Один з них має бути основним, останні - додатковими. Основною повинен відповідати головній меті функціонування. Додаткові - характеризувати стан елементів, просторово-часові і інші умови або обмеження.

Якщо складні системні операції, складові в цілому функціонування системи, можуть бути розділені на складові частини, кожна з яких оцінюється незалежно, як рішення приватної задачі, то в цьому випадку застосовуються головний і приватні показники. Приватними показниками оцінюється ефективність вирішення приватних завдань. Головним показником оцінюється кінцевий результат.

У загальному випадку основні, додаткові, головні або приватні показники ефективності (цільові функції) мають бути критичними (чутливими) до структури системи, властивостей і кількості її елементів. Лише тоді їх можна використовувати для оцінки міри досягнення мети різних альтернативних варіантів функціонування системи і лише тоді можуть бути отримані правильні для ухвалення рішень рекомендації. Після вибору показника ефективності (цільовій функції), що є фактично математичною мірою мети дослідження системи, записаної, як правило, у вигляді функціонала від характеристик системи, формулюється математична постановка завдання.

ТЕМА 5: КОНЦЕПЦІЯ 4-Х “І”

Концепція «Чотири І» – це складноструктурована в просторі станів (виробництво - застосування – розвиток) концепція, або, як випливає з визначення, – головний задум для систематичного освітлення діяльності, пов'язаної зі створенням, застосуванням і розвитком засобів обчислювальної техніки.

Розвиток виробництва, інтереси суспільства в цілому диктують необхідність удосконалювання інформаційного обміну і технології інформаційного обслуговування. Очевидною стає роль інформації як діючої сили, що робить істотний вплив на прискорення всіх процесів, що відбуваються в суспільстві.

Складові концепції «чотири І»:

1) інформатизація

2) інтелектуалізація

3) інтеграція

4) індивідуалізація.

1) Інформатизація (як складова концепції “чотири І”, у питаннях застосування засобів обчислювальної техніки) – відбиває нову якість і споживчі властивості, поява яких ними обумовлена.

У концепції інформатизації, що має складну структуру, можна виділити деякі рівні:

- моделювання;

- обмін інформацією з метою прийняття рішень;

- інформаційне обслуговування та ін.

Кожний із цих рівнів характеризується своїми класифікаційними ознаками:

- рівень моделювання – появою нових вимог і нових послуг, формуванням умов безупинного зниження експлуатаційних витрат;

- рівень обміну інформацією – показниками, що ставляться до інформації: повнота, точність, істотність, своєчасність, промовистість; потім – показниками, що характеризують інформацію як товар (масовість, доступність, тиражування, економічність). Характерно, що інформація при використанні не зменшується, а збільшується.

Така частина показників характеризує якість інформаційного обслуговування:

- більш висока точність і повнота інформації;

- своєчасність її одержання;

- відповідність інформації аналізованому питанню (істотність і релевантність); промовистість;

- активність сприйняття;

- спонукання до цілеспрямованих дій.

Інформація необхідна для прийняття тих або інших рішень; вона трансформується в результаті аналізу й узагальнення в знання.

Прийняттю рішень передують етапи аналізу, оцінки ситуацій, прогнозу, моделювання й оптимізації.

Критерій якості інформатизації згодом може змінитися, у зв'язку з чим одні показники зникнуть, а інші з'являться, але сама концепція безумовно буде зберігатися тривалий час.

2) Інтелектуалізація – це складова концепції “чотирьох І”. Розуміючи під інтелектуалізацією засобів обчислювальної техніки такі їх властивості, як спроможності до класифікації об'єктів, розпізнаванню образів і ситуацій, логічному висновку, накопиченню, збереженню і видачі знань, до спілкування з користувачем на природній мові, стає зрозуміло, чому засоби обчислювальної техніки спеціалісти вважають універсальними технічними засобами посилення інтелектуальних спроможностей людини.

Керівна ідея або головний задум (концепція) у застосуванні засобів обчислювальної техніки тезовано сформульована в такий спосіб: «використання засобів обчислювальної техніки максимально ефективно там, де для прийняття рішень необхідні інтелект і знання».

3) Інтеграція – одна з складових концепції “чотири І”. Вона виникла з аналізу стану і перспектив розвитку народного господарства. Тенденція розвитку така: як значні, так і дрібні господарські утворення для свого ефективного існування потребують посилення взаємодії, узгодженості, динамічності і гнучкості. Інтеграція у виробництві й у сфері міжнародного поділу праці різко посилює горизонтальні зв'язки, що збільшує сінергічний ефект. Володіючи практично необмеженими можливостями для накопичення і збереження інформації, швидкодією при переробці інформації, засобам обчислювальної техніки властиві також багато інтеграційних властивостей.

Саме за рахунок цих можливостей засобів обчислювальної техніки була сформульована ідея інтеграції в застосуванні їх як синтезу більш поглибленого, інтеграційного розгляду виробничих і інформаційних процесів, прагнення створювати багаторівневі комплексні системи автоматизації, вимоги розширення властивостей.

4) Індивідуалізація – завершальна складова концепції “чотирьох І”. Аналіз тенденцій розвитку суспільства показує, що усе більше значення додається людському чиннику, урахуванню індивідуальних особливостей користувачів, прагнення до функціональної і особистої орієнтації, прагнення до самообслуговування.

Відповідно до цього індивідуалізація як концепція застосування засобів обчислювальної техніки – прагнення й орієнтир у створенні систем і устроїв на базі засобів обчислювальної техніки на функціональну і особисту орієнтацію.

ТЕМА 6: СИСТЕМНИЙ АНАЛІЗ ПРОЦЕСІВ ФУНКЦІОНУВАННЯ СИСТЕМ

Системний аналіз – це методологія дослідження складних об'єктів як систем.

Методологія (від грецьк. methodos – шлях дослідження чи пізнання; logos – вчення) – це систематизована сукупність підходів, способів, методів, прийомів та процедур, що застосовуються в процесі наукового пізнання та практичної діяльності для досягнення наперед визначеної мети.

Головне завдання системного аналізу – це управління та прийняття рішень.

Головна концепція системного аналізу – це системний підхід.

Системний підхід – це методологія вирішення складних проблем.

Суть системного підходу, який є методологією рішення складних проблем, реалізується в три великих етапи:

· Систематизація (цілей задач, моделей, методів і т.д.) на базі проведення класифікації та упорядкування (м.б. декомпозиції);

· Використання формалізованого поняття «система» (<вхід>- <перетворення> - <вихід>) і проведення математичних і комп'ютерних експериментів;

· Застосування методології цілеориєнтування системи (<цілі>↔<засоби>), що деталізується в більш конкретну структуру:

(<цілі> ↔ <задачі моделі> ↔ <методи алгоритми> ↔ <завдання технічні засоби>).

Використання поняття “система”. Вище було визначене поняття “система”. Для опису системи повинні бути точно визначені категорії і поняття, що дозволяють уявити її формальними засобами. З одного боку, система являє собою відособлену частину середовища, що може бути розглянута як окремий об'єкт, що виконує визначені функції. З іншого боку, система є сукупністю елементів і зв'язків між ними.

Елементи системи в ряді випадків можуть бути розчленовані на більш “дрібні” елементи і т.д. Внутрішній розподіл системи на елементи і зв'язки дозволяє спростити процес створення або дослідження системи.

При створенні (дослідженні) системи відповідно до системного підходу необхідно використовувати поняття “цілеорієнтованість”, що розуміє проходження визначеної цілі протягом усього процесу створення або дослідження.

Реалізація даної методології дозволяє модельовані процеси представити у вигляді деякої сукупності моделей:

· «частина-ціле», тобто машинобудівна модель (морфологічна структура), що відбиває властивості будови системи – машини, пристрою, агрегату, виробу і т.д.(цільова категорія);

· функціонування – модель функціональної динаміки, що відбиває властивості функціонування як процесу досягнення цілей (стійкість, оптимальність, надійність і т.д.);

· витрати ресурсів – модель ресурсної динаміки (процесів використання - експлуатації);

· модель розвитку (адаптаціz, пристосування, самоорганізаціz, функціонування з використанням усіх видів змін, спрямованих на підтримку працездатності (значень величин, параметрів структури, функції, мети і т.д.)).

Уся сукупність відносин як у межах кожної з моделей, так і між ними може бути представлена системною моделлю.

Наприклад, процес будови (розбирання) складного виробу з погляду цілеполягання (ціледосягнення) може бути представлений моделлю у виді деякої деревоподібної мережі (граф), що складається з дуг відносин <частина> – <ціле>, результатів застосування операції об'єднання (зборки):

E= UE_i,

^iєІ

де і – пробігає індексну множину І, що представляє сукупність об’єднаних частин E_i у ціле (систему виробу).

Існує два підходи до дослідження систем або наступні дві задач:

Пряма задача

Дано:

- мета функціонування системи;

- елементи системи і їх властивості;

- елементарні (неподільні) операції, що дозволяють вирішити завдання або виконати функції за допомогою елементів, що беруть участь в них, відповідно до їх властивостей.

Необхідно визначити сукупність і послідовність системних операцій, складових функціонування системи або її структуру і що дозволяють досягати мета системи.

Відзначимо, що для прямого завдання формулювання мети функціонування системи залежить від складу системи, тобто від кількості елементів і їх властивостей. Дуже часто при цьому виникають протиріччя між складом системи і можливістю створити структуру, що дозволяє досягти певну заздалегідь мету. Тому при рішенні прямої задачі доводиться коректувати мету функціонування, яку можна досягти, виходячи із заданого складу системи.

Як правило, пряме завдання вирішується при дослідженні існуючих систем, коли відомий склад і необхідно удосконалювати її структуру так, щоб підвищити, наприклад, ефективність функціонування системи.

Обернена задача

Дано:

- мета функціонування системи;

- сукупність і послідовність системних операцій тих, що виконують функції системи і складових її структуру, що дозволяє досягти мети функціонування системи.

Необхідно визначити:

- елементарні (неделимые) операції, що становлять системні (складені) операції;

- властивості елементів, що дозволяють їм виконувати елементарні операції;

- елементи системи, що мають вибрані властивості.

Зворотне завдання вирішується в основному при створенні нових, до цих пір, не існуючих систем.

ТЕМА 7:ОСНОВИ СИСТЕМНОГО ПРОЕКТУВАННЯ

Системне проектування — це методологія побудови проектів складних ОНТ як цілеспрямованих систем у базисах системних властивостей, системних ресурсів та структурах життєвих циклів ОНТ.

Під цілеспрямованою системою слід розуміти таку систему, результат функціонування якої спрямований на досягнення певної цілі (або деякої сукупності цілей).

Визначаючи "рішення проблеми" як "цілеспрямовану систему", системний підхід тим самим дозволяє уявити процес рішення проблеми як процес конструювання і використання системи відповідно до етапів її життєвого циклу.

При цьому ефективність рішення проблем залежить у першу чергу від методів, застосовуваних для виконання функцій рішення складових проблеми. "Пропускна спроможність", точність й інші характеристики методів, що входять у дану цілеспрямовану систему, повинні бути збалансовані між собою, а витрати на них повинні відповідати виграшу.

У будь-якій системі існує два основних і різноманітних по ролі підпроцеса:

- основний процес;

- зворотній зв'язок, а також вхід, вихід і обмеження.

Поняття процесу є центральним поняттям системного підходу в рішенні проблеми, що являє собою різницю між існуючою і бажаною системою.

Основний зміст системного підходу полягає не стільки у формальному математичному апараті, що описує "системи", "рішення проблеми" і не в спеціальних математичних методах, а в його концептуальному, тобто понятійному апараті, у його ідеях, підході й установках.

У загальному випадку, виходячи з концепцій системного проектування, рішення проблеми включає наступні етапи:

- ідентифікація (виявлення) проблеми;

- оцінка актуальності проблеми;

- визначення цілі (установлення критеріїв і обмежень);

- виявлення (розкриття) структури системи і її дефектних елементів;

- визначення структури системи для побудови набору варіантів;

- перебування, оцінка і вибір варіанта (альтернативи);

- складання рішення (визначення процесу реалізації);

- узгодження знайденого рішення (визнання рішення колективом виконавців і керівників);

- запуск процесу реалізації рішень (реалізація рішення);

- керування процесом реалізації рішення;

- оцінка реалізації і її наслідків (прочерки ефективності).

Сформульовані етапи рішення проблеми носять загальний характер, тому що поняття "складна система" містить у собі на тільки технічні системи, але і підприємства, різноманітні промислові організації як системи (біологічні системи, системи знань і ін).

ТЕМА 8: КОМПЛЕКС МОДЕЛЕЙ ОБ'ЄКТІВ НОВОЇ ТЕХНІКИ В ЗАДАЧАХ СИСТЕМНОГО ПРОЕКТУВАННЯ

Модель логіко-динамічної системи зі структурою, що змінюється

Дослідженню задач складових процесів проектування складних систем присвячено чимало праць у вітчизняній та зарубіжній літературі. В класі складних систем виділено системи з багатьма рівнями і складним характером взаємодії підсистем, що мають дискретну природу функціонування типу мереж, складні системи, які зображено моделями з імовірнісними характеристиками, дискретно-неперервні системи та ін.

Перелічені різновиди моделей складних систем розглядалися для опису законів функціонування окремих класів ОНТ. Але математично пристосувати їх для дослідження інших процесів (наприклад, витрачання та відновлення ресурсів ОНТ) і властивостей (досяжності цілей, надійності виконання операцій та ін.) не було можливості. Моделі, що пропонуються нижче, дають змогу розв'язувати багато прикладних задач моделювання ОНТ, в яких знайдено достатньо адекватні умови математичного узгодження диференціаль­них динамічних моделей з автоматними, а також їх «гібридів» зальтернативними мережами, дістаючи, таким чином, моделі динамічних операцій М_ДО^ОБ. Це дає змогу побудувати й дослідити пакети останніх.

Розглянемо динамічну диференціальну систему (ДДС), яка описується упорядкованою шісткою елементів:

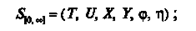перші чотири з них — множини, в категоріях яких задається відображення

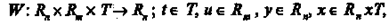інтерпретоване відношеннями між властивостями вимірю­ваних величин (ract, (вхід и (t), стан х (t), вихід у (t))

Отже, аксіоматика ЛДС дає змогу «вирватися» зі сфери дослідження внутрішніх властивостей асинхронних автоматів і розв'язувати задачі «зовнішнього» проектування ДЦС та синтезу керованої структури складних об'єктів з використанням апарату моделювання областей досяжності ЛДС і дискретних переходів на множинах F{f_s } і U{и_к(t)}.

У задачах системного проектування ОНТ в широкому розумінні моделі ЛДС використовуються для дослідження агрегатів чи підсистем S_i Î S. Кожну із сукупностей підсистем ОНТ (i = 1, 2,..., N) можна визначити за допомогою домінуючої підсистеми S_i, категорії якої визначають процес і факт досягнення мети G (наприклад, підсистеми керування рухом у просторі для саморушних машин).

Задача керування ЛДС об'єднує і математично узгоджує дві ієрархічно упорядковані і математично різнорідні задачі:

- синтез вхідного и_к(t) впливу, и_кÎU, для локального структурного стану q_vi зі стаціонарною функцією (нижній рівень);

- повна упорядкованість дискретних переходів на скінченній множині структур функцій f_sÎF (верхній рівень).

Слід зазначити, що відомий принцип Беллмана «(керування и_к є функція фазового стану х(t), тобто и_к = к(x))» недостатній в разі «ієрархічних систем виділеного логіко-динамічного класу». Він може мати таку форму: «керування є функція упорядкованої послідовності структурних станів q_v (верхній рівень) та фазових станів х(t) (нижній рівень)».

Задача повного упорядкування (керування верхнього рівня) зводиться до синтезу закону функціонування ініціального скінченного автомата А{А",А^f) як комбінованої і частини системи S(S_i). Вона розв'язується апаратом моделювання систем ЛДР.

Задача глобальної оптимізації ЛДС включає в себе дві ієрархічні упорядковані підзадачі:

- оптимальне упорядкування скінченної сукупності структур f_s системи F{f_s } (верхній рівень);

- синтез оптимальних керуючих впливів и_к (t), и_кÎU при локальній стаціонарності структури f_s (нижній рівень).

Сумісне дослідження методами моделювання цих задач виключає необхідність повного перебору переходів на множині F{f_s }. Цілеспрямованість процесів керування в ЛДС, що вводиться в закон функціонування системи S(S_i) шляхом упорядкування підцілей G_μ, конструктивно виражається перетином підобластей існування локальних розв'язань системи ЛДР. Ця властивість ЛДС, отримана як наслідок їх аксіоматичного визначення, виділяє із множини логічних автоматів ініціальний автомат Мура в складі комбінаторної частини ЛДС.

«Машинобудівна» модель (морфологічна структура ОНТ)

У «машинобудівній» конструкції об'єкта М_МБ^ОБ одним із основних відношень є відношення <частина — ціле>, яке можна зобразити теоретико-множинною операцією об'єднання А = U А_і, де і пробігає індексну множину І, іÎІ, що становить сукупність частин, які об'єднують А_і в одне ціле — А. Для «машинобудівної» моделі ОНТ характерною є багатоярусна піраміда таких відношень.

При багаторазовому вкладенні операцій об'єднання М_МБ^ОБ зручніше зобразити графом

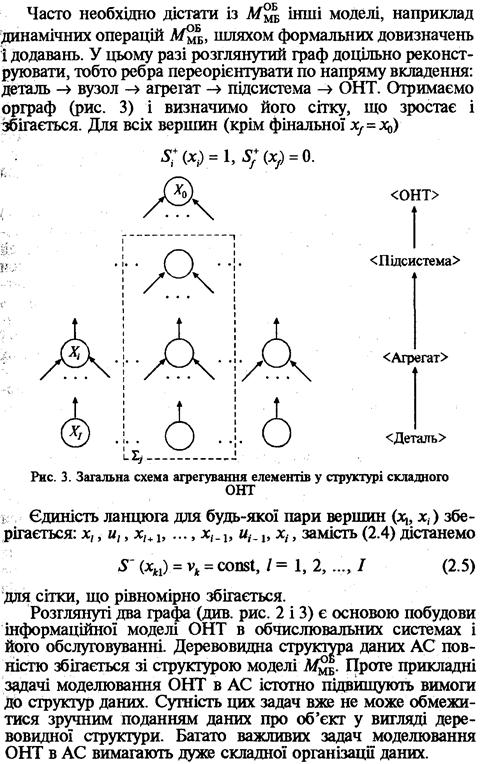
Виділимо дві фундаментальні категорії моделей ОНТ, що визначені структурою об'єкта («ОНТ складається із...») та його функціональним призначенням («ОНТ створений для...»).

Для першої категорії («ОНТ складається із...») характерними є точність опису та точність, досяжні завдяки класифікаціям елементів, починаючи із деталей — висячих вершин х_і — і закінчуючи фінальною вершиною х_f — ОНТ в цілому. Використовуючи апарат теорії інформа­ції, можна ввести ступінь структурної складності ОНТ для моделей типу М_МБ^ОБ.

Для другої категорії моделей («ОНТ створений для...») опис має велику різноманітність, оскільки мовою цих створених моделей повинні бути представлені категорії цілей функціонування програми використання ОНТ і процеси функціонування ОНТ, процеси витрачання ресурсів, внутрішні властивості ОНТ (керованість, стійкість, досяжність та ін.) та інтегральні (технічна готовність, надійність, відновлюваність та ін.). Звідси ясно, що комплекс моделей цієї категорії вимагає адекватної різноманітності структур даних для моделювання й надто їх складної організації.

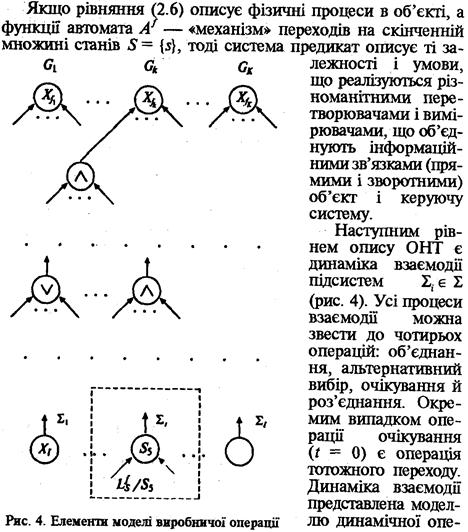
Моделі функціональної динаміки

ТЕМА 9. МЕТОД АНАЛІЗУ ІЄРАРХІЙ

У процесі розв’язання складних проблем застосовуються систематичні процедури, однією з яких є метод аналізу ієрархій. Загальним для цих процедур є використання декомпозиції, щоб зменшити число можливих помилок у процесі отримання інформації від експерта. Справа в тому що експерт має обмежені можливості щодо оцінювання якості багатьох альтернатив, значно краще буде, якщо процедура отримання необхідної інформації складатиметься з нескладних кроків. Метод аналізу ієрархій приводить до структури у вигляді мультидерева, дозволяє уникнути складних порівнянь, замінивши їх попарними, і, крім того, має засоби для перевірки послідовності (несуперечливості) тверджень експерта. Цим пояснюється широка розповсюдженість методу, його дійсно системний характер та велика кількість практичних застосувань.

9.1 Ієрархічне представлення складної проблеми

Метод аналізу ієрархій (МАІ) –це систематична процедура, що ґрунтується на ієрархічному представленні елементів, які визначають суть проблеми. Проблема розбивається на простіші складові з наступним оцінюванням особою, що приймає рішення (ОПР), відносного ступеня взаємодії елементів отримуваної ієрархічної структури. В МАІ використовуються жорсткі оцінки в шкалі відношень. МАІ будується на принципі ідентичності та декомпозиції і включає процедури синтезу множинних тверджень, отримання пріоритетності критеріїв та знаходження альтернативних рішень.

Принцип ідентичності та декомпозиції – передбачає структурування проблем у вигляді ієрархії або мережі як першого етапу МАІ.

Можна виділити ряд модифікацій МАІ, що визначаються характером зв’язків між критеріями й альтернативами (сценаріями), розташованими на найнижчому рівні ієрархії, а також методом порівняння альтернатив. За характером зв’язків між критеріями й альтернативами визначається два типи ієрархій: перший та другий.

У МАІ є три методи порівняння альтернатив:

- попарне порівняння;

- порівняння альтернатив щодо стандартів;

- порівняння альтернатив копіювання.

Останні два методи використовуються в тому випадку, коли з тих чи інших причин відсутні оцінки деяких альтернатив за деякими критеріями.

Проблема, що її потрібно вирішити, у більшості випадків зводиться до обґрунтування вибору певної альтернативи з числа можливих, які характеризуються складною ієрархією аспектів та критеріїв. Останнім рівнем цієї ієрархії - по суті мультидерева - є рівень листя, на якому знаходяться власне альтернативи, а передостаннім, безпосередньо з ним пов’язаним – рівень критеріїв оцінювання якості альтернатив. Вищі рівні відображають агреговані критерії та аспекти проблеми, а кореневі дерева відповідає власна проблема, що повинна бути розв’язана.

Основним варіантом представлення проблеми є ієрархія з однаковим числом та функціональним складом альтернатив під критеріями (перший тип ієрархій), тобто ієрархія, в якій альтернативні варіанти оцінюються за всіма критеріями передостаннього рівня. У тих випадках, коли з тих чи інших причин не всі альтернативи можуть бути оцінені за всіма критеріями, використовуються модифікації методу аналізу ієрархій.

У загальному випадку МАІ побудова ієрархії починається з окреслення проблеми дослідження. Далі будується власне ієрархія, що включає мету (призначення), якій відповідає корінь ієрархії, проміжні рівні (аспекти мети, метакритерії, критерії) і альтернативи, що формують найнижчий ієрархічний рівень (листя). На рис. 9.1 наведений загальний вигляд ієрархії, де Q –елементи ієрархії, B – альтернативи. Верхній індекс в елементів указує рівень ієрархії, а нижній індекс – їхній порядковий номер.

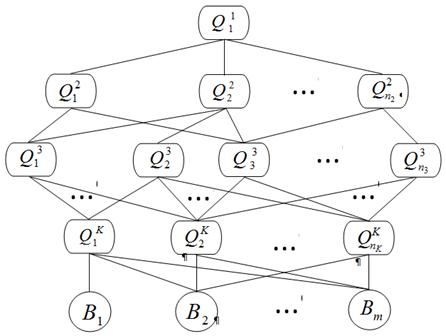
Рисунок 9.1. Загальний вигляд ієрархії в МАІ

9.2 Локальні пріоритети та методи їх отримання

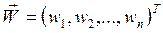Елементи задачі в МАІ порівнюються попарно відносно їх дії (ваги, інтенсивності) на спільну для них характеристику. Якщо - множина елементів, а - вектор відповідних їм ваг або інтенсивностей, то елементи матриці їх порівняльної важливості визначаються за формулою: 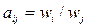. Якщо 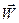невідомий, то попарні порівняння реалізуються на основі суб’єктивних тверджень, що оцінюються за певною шкалою, і за цими даними знаходиться.

У випадку ієрархічного представлення проблем матриця А складається для порівняння відносної важливості критеріїв наступного рівня відносно елементів попереднього, тобто процес побудови матриць попарних порівнянь шляхом опитування експертів реалізується «згори-донизу».

В ієрархії виділяють елементи двох типів: елементи-предки і елементи-нащадки. Елементи-нащадки впливають на відповідні елементи попереднього рівня ієрархії, що є стосовно них елементами-предками. Матриці парних порівнянь А будуються для елементів-нащадків, що належать до відповідного елемента-предка. Елементами-предками можуть бути елементи, що належать будь-якому ієрархічному рівню, крім останнього, на якому розташовані, як правило альтернативи (див. рис. 9.1). Парні порівняння реалізуються в термінах домінування одного елемента над іншим. Отримані твердження висловлюються в цілих числах з урахуванням дев’ятибальної шкали. Значення елементів цих матриць визначаються в результаті опитування експертів. Як результат, після порівнянь в МАІ для множини нащадків кожного предка отримується позитивна обернено-симетрична матриця А.

Для реалізації суб’єктивних парних порівнянь в МАІ використовується наступна дев’ятибальна шкала (табл. 9.1).

Таблиця 9.1

Шкала відносної важливості МАІ

Бал k	Визначення	Примітка
	Рівна важливість	Рівний вклад двох видів діяльності в мету
	Помірна перевага	Легка перевага одного виду діяльності над іншим
	Суттєва перевага	Відчутна перевага одного виду діяльності над іншим
	Значна перевага	Практично значна перевага одного виду діяльності над іншим
	Дуже велика перевага	Очевидна перевага-домінування одного виду діяльності над іншим
2,4, 6,8	Проміжні значення	Застосовуються в перехідних випадках
	Обернені величини	Використовуються для оцінки непереважаючих видів діяльності

Заповнення квадратної матриці попарних порівнянь А відбувається наступним чином:

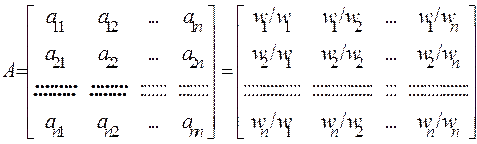. (9.1)

Матриця А будується для кожного елемента-предка, її розмір визначається кількістю безпосередніх нащадків n у цього елемента-предка. Якщо елемент-нащадок 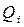домінує (є кращий ніж інший елемент-нащадок цього предка), то експерт визначає ступінь домінування, використовуючи наведену вище шкалу в термінах визначень, і відповідне значення в балах (див. табл 9.1) розраховується і присвоюється елементу 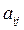, а значення 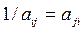-- елементу (оскільки природним чином, якщо 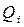є кращий ніж в 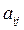разів, то «кращий» за 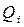в 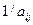разів, або, що еквівалентно, «гірший» за 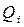в разів). 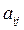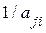Отже, матриця попарних порівнянь є обернено-симетричною, тобто для всіх її елементів = , а елементи головної діагоналі є одиницями.

При порівнянні критеріїв зазвичай питають, який з критеріїв є важливішим; при порівнянні альтернатив за критеріями -- яка з альтернатив є бажанішою; при порівнянні сценаріїв, які отримуються з критеріїв,-- який зі сценаріїв є більш ймовірним.

У тих випадках, коли важко розрізнити стільки проміжних градацій (див .табл. 9.1), може використовуватися шкала з меншим числом градацій.

Локальним завданням для нас є визначення «ваги» кожного з нащадків відносно всіх вершин ієрархії (за винятком листя). Звичайно, було б ідеальним варіантом, якщо б особа, що приймає рішення, чи експерт могли б безпосередньо вказати ці ваги. Однак, якщо елементів-нащадків більше, ніж три, твердження експерта будуть суперечливими та дуже ненадійними, що викликано психологічними особливостями людини-експерта та підтверджене багатьма дослідженнями. Для експерта значно простіше здійснити ряд попарних порівнянь нащадків між собою, а ніж спробувати відразу ж присвоїти їм певні значення «ваг», які відображають вклад того чи іншого елемента–нащадка в елемент-предок. Цим і пояснюється необхідність застосування методу попарних порівнянь, тому що ця інформація надалі використовується для отримання значень «ваг» та оцінювання послідовності тверджень експерта.

Цей крок і є кроком формування локальних пріоритетів на основі матриць попарних порівнянь А, які відображають відносний вплив множини елементів наступного рівня на елемент безпосередньо попереднього рівня. Змістовно цьому відповідає знаходження бажаності, сили впливу, цінності чи ймовірності для кожного окремого об’єкта-нащадка відносно безпосереднього об’єкта - предка.

Локальні пріоритети отримуються шляхом обчислення множини X головних власних векторів для кожної з обернено-симетричних матриць ієрархії та нормалізації результату.

Обчислення головного власного вектора позитивної квадратної матриці реалізується на підставі визначення-рівності

,

де - максимальне власне значення матриці А.

Для позитивної квадратної матриці А правий власний вектор , що відповідає максимальному власному значенню , можна обчислити з точністю до постійного співмножника за формулою:

k=1,2,…,

де 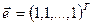- одиничний вектор; с -константа.

Обчислення власного вектора за цією формулою проводяться до досягнення заданої точності обчислення за співвідношенням

,

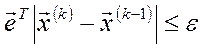де k - номер ітерації обчислення; ε - припустима точність обчислення. З достатньою для практики точністю можна вважати, що ε=0,01 незалежно від порядку матриці А.

Максимальне власне значення обчисляється за формулою:

. (9.2)

За наведеними формулами можна сконструювати ітераційний алгоритм, що обчислюватиме значення головного власного вектора матриці попарних порівнянь А. Для цього можна також використати відповідний математичний програмний пакет, наприклад, Mathcad.

Існує простіший спосіб наближеного обчислення пріоритетів шляхом обчислення середнього геометричного рядків матриці попарних порівнянь з наступною нормалізацією всіх складових отриманого вектора за формулою:

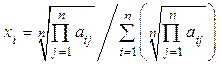
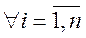(9.3)

Після отримання значень власного вектора вони використовуються для подальших обчислень.

9.3 Оцінювання послідовності тверджень експерта

У процесі формування матриці попарних порівнянь А на матрицю накладається обмеження оберненої симетричності, тобто за умовою а_ij = 1/ а_ij, що сприяє поліпшенню однорідності та послідовності тверджень експерта. Тобто в числових твердженнях, якщо один елемент в m разів переважає інший, то останній в 1/ m разів переважає перший (або в m разів гірший). У практичних задачах кількісна (кардинальна) і транзитивна (порядкова) однорідність (узгодженість) порушується, оскільки експерт оцінює переваги шляхом попарних порівнянь, а тому рівність

а_ij а_jk = а_ik,

що повинна була б виконуватись для всіх i,j,k з урахуванням формули (9.1), буде порушуватися. Чим більше порушення цих рівностей, тим меншою мірою ми можемо довіряти результатам опитування експерта, і це свідчитиме, насамперед, про суперечливість тверджень експерта або ж про некомпетентність в даній предметній області.

При порушенні однорідності ранг матриці попарних порівнянь А відмінний від одиниці (rank A >1), і вона буде мати декілька власних значень, а умова оберненої симетричності забезпечить невід’ємність всіх компонент головного власного вектора 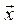. Однак при невеликих відхиленнях тверджень від однорідності одне з власних значень буде істотною більше за інші і приблизно дорівнюватиме порядку n матриці. Отже, для оцінки однорідності тверджень експерта доцільно використати відхилення величини максимального власного значення λ_max (9.2) від порядку матриці n.

Отримана в результаті опитування експерта матриця А буде неузгодженою, тобто відображати повну непослідовність тверджень експерта, яка в реальних умовах наявна завжди. Корисним результатом для оцінювання неузгодженості є індекс узгодженості, який дає інформацію про ступінь порушення числової та транзитивної (порядкової) узгодженості. Якщо відхилення від узгодженості перевищують межі, то доцільно їх перевірити в матриці. Індекс узгодженості розраховуємо за формулою:

I_u = 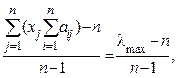(9.4)

звідки значення λ_max замість формули (9.2) може бути розраховано за формулою:

(9.5)

Обчислений індекс I_u (9.4) порівнюємо зі значенням, яке утримується за умови випадкового вибору кількісних значень з шкали 9, 8, 7, …, 2, 1, 1/2, 1/3, …, 1/7, 1/8, 1/9 зі збереженням умови оберненої симетричності випадкової матриці. Ці значення отримані з використанням генератора псевдовипадкових чисел програмним шляхом: генерується випадкова матриця заданого розміру n, в якій діагональ заповнюється одиницями, а верхня трикутна частина – числами послідовності 9, 8, 7, …, 2, 1, 1/2, 1/3, …, 1/7, 1/8, 1/9, що розподілені рівномірно з ймовірністю виникнення кожного значення, рівною 1/17. Нижня трикутна складова заповнюється, виходячи зі співвідношення а_ij = 1/ a_ji, що визначає обернено-симетричну матрицю. Для згенерованої таким чином випадкової матриці А розраховується значення індексу узгодженості тверджень експерта I_u. Процедура повторюється велику кількість разів з розрахунком середнього значення (математичного очікування), яке й вноситься до таблиці. Середні значення індексу узгодженості [М(I_u)] для випадкових матриць різного розміру наведені в табл.9.2.

Таблиця 9.2

Значення індексу узгодженості для випадкових матриць

Розмір матриці
Випадкова узгодженість			0,58	0,90	1,12	1,24	1,32	1,41	1,45	1,49	1,51	1,48	1,56	1,57	1,59

Відношення узгодженості є часткою від ділення індексу узгодженості I_u на відповідне значення випадкової узгодженості М(I_u):

I₀ = I_u /М(I_u), (9.6)

де М(I_u) – середнє значення (або математичне очікування) індексу узгодженості для випадкової матриці.

Якщо отримане значення є меншим ніж 10%, то рівень узгодженості може вважатися задовільним. У деяких випадках можна обмежитися 20%.

9.4 Алгоритм синтезу глобальних пріоритетів альтернатив

Основним завданням МАІ є розрахунок глобальних пріоритетів альтернатив, тобто пріоритетів альтернатив відносно всієї ієрархії. Вихідними даними при цьому є результати опитування експертів у вигляді матриць попарних порівнянь А при всіх вузлах ієрархії за винятком рівня листа - альтернатив.

Ієрархічний синтез використовується для зважування власних векторів матриць парних порівнянь альтернатив вагами критеріїв (елементів Q_j), що наявні в ієрархії, а також для обчислення загальних пріоритетів альтернатив. У результаті побудови ієрархії та реалізації парних порівнянь для всіх вершин ієрархії Q_j⁽ⁱ⁾ окрім листя (що відповідає множині альтернатив) побудовані матриці парних порівнянь А _j⁽ⁱ⁾, де i (i =) – номер рівняння ієрархії (корінь ієрархії відповідає 1-му рівню, s – номер передостаннього рівня ієрархії, останній рівень s+1 – є рівнем альтернатив); j (j =) – індекс вершини всередині i- го рівня.

Обчислення глобальних пріоритетів відбувається згідно наступного алгоритму, який узагальнює описане вище.

АЛГОРИТМ СИНТЕЗУ ГЛОБАЛЬНИХ ПРІОРИТЕТІВ АЛЬТЕРНАТИВ:

1. Визначаємо головні власні вектори для всіх матриць парних порівнянь ієрархії з заданою точністю . Для цього використовуємо наведені вище в п.9.2 співвідношення для конструювання відповідного алгоритму та написання програми, або ж формулу (9.3) для найближчого розрахунку, або ж математичний спеціалізований пакет типу Mathcad.

Для s-го рівняння (j є J ^(S)) вже є векторами пріоритетів альтернатив відносно елементів цього рівня ієрархії, і тому виконується початкове присвоювання:

де – вектор пріоритетів альтернатив відносно елементу Q_j^(S); J^(S) – множина індексів елементів s-го рівня. Для вершин інших рівнів відповідні головні власні вектори відображають переваги (пріоритети) елементів певного ієрархічного рівня відносно елементів наступного вищого рівня ієрархії, з якими вони пов'язані безпосередньо.

2. Починаємо ієрархічний синтез з рівня s-1 (тому що для s-го рівня є векторами пріоритетів альтернатив відносно цього рівня ієрархії), тому номер поточного рівня ієрархії (початкове присвоювання) і = s-1.

3. Для всіх вершин і -го рівня розраховуємо вектори пріоритетів альтернатив 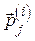(j є J ^{( i )}). Для цього для кожного елементу будуємо прямокутну матрицю Р _j⁽ⁱ⁾ з векторів пріоритетів альтернатив елементів ієрархії, що є прямими нащадками елементу :

P _j⁽ⁱ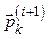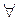⁾ ={} (k є J^{(i+ 1)}), (9.7)

де J ^{(i +1)} – множина індексів елементів (і+1)-го рівня, які є безпосередніми нащадками елементу Q_j^(і).

Розраховуємо вектори глобальних пріоритетів альтернатив відносно елементу Q_j^(і) ієрархії:

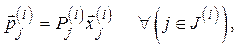(9.8)

де

=

4. Присвоюється і=і- 1. Якщо і > 0, то переходимо до п.3, продовжуючи розрахунки. В іншому випадку (і =0) досягнутий корінь ієрархії Q ₁⁽¹⁾, і вектор пріоритетів альтернатив є результуючим вектором пріоритетів альтернатив відносно ієрархії, тобто вектором глобальних пріоритетів альтернатив.

Перерахунок векторів пріоритетів 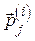можна здійснювати як перерахунок головних власних векторів елементів ієрархії, якщо немає необхідності зберігати їх для подальшого аналізу.

Оцінювання однорідності ієрархії

Після розв'язання задачі ієрархічного синтезу оцінюється однорідність ієрархії загалом за допомогою підсумовування показників однорідності (узгодженості) всіх рівнів, приведених шляхом «зважування» до першого ієрархічного рівня, де знаходиться коренева вершина. Число кроків алгоритму по обчисленню однорідності (узгодженості) визначається конкретною ієрархією.

Визначення відношення однорідності (відношення узгодженості) для всієї ієрархії здійснюється за формулою

I₀ = I_u /М(I_u),

де М(I_u) – підсумковий індекс однорідності (узгодженості) ієрархії при випадковому заповненні матриць попарних порівнянь. Розрахунок М(I_u) при випадковому заповненні матриць виконується за формулою аналогічною до формули визначення підсумкового індексу однорідності I_u (див. приклад 9.5.5).

При практичній реалізації методу МАІ слід мати на увазі, що для обґрунтованих числових порівнянь оптимальною кількістю є 7±2 елемента в рівні ієрархії. Якщо є більша кількість об'єктів, то необхідно застосовувати ієрархічну декомпозицію. У цьому випадку елементи ґрунтуються по ≈7 елементів у групі. Елемент з найбільшою вагою в класі включається також в наступний клас елементів з більшими вагами і забезпечує однорідність шкали.

Перевагами МАІ є його вклад в аналіз структури проблеми та чітке висловлення тверджень. Загальна мета (фокус) проблеми відповідає вищому рівню ієрархії. Наступний рівень – найважливіших критеріїв, далі - підкритеріїв, і нарешті рівень альтернатив. Окрім того, в деяких випадках після рівня загальних критеріїв можливе включення рівнів акторів, цілей акторів, політик акторів.

Дата добавления: 2014-01-07