
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклади
|
|
|
|
9.5.1 Приклад 1. (Побудова матриці попарних порівнянь А).
Для порівняльного оцінювання чотирьох моделей комп'ютерів (А,В,С,D) експерт провів попарні порівняння та дав такі оцінки у вигляді тверджень (див. табл..9.1):
1. Модель С помірно переважає модель А.
2. Модель В помірно поступається моделі С.
3. Модель А значно переважає модель D.
4. Превага моделі С над D знаходиться між значною та дуже великою.
5. Модель А помірно поступається моделі В.
6. Модель В помірно переважає модель D.
Необхідно побудувати матрицю попарних порівнянь.
Розв'язання.
Перевіримо, чи на основі цих тверджень можна побудувати повну матрицю попарних порівнянь А. Серед порівнянь немає симетричних, тобто якщо елемент а порівнюється з елементом b, то немає жодного такого твердження, щоб елемент b порівнювався з елементом а. Якщо такі твердження зустрічаються, то вони рахуються як одне твердження, а пряма оцінка такого порівняння обчислюється у вигляді середнього геометричного прямої та оберненої до оберненої оцінок. Оскільки незалежних стосовно симетрії тверджень є 6; а потрібною є така ж кількість порівнянь (розраховується за формулою: n 2/2 - n /2, де n – кількість альтернатив, що оцінюються), то матрицю А можна побудувати повністю.
Побудуємо матрицю А, в якій рядки та стовпчики будуть відповідати моделям А,В,С та D відповідно. Оскільки об'єкт є рівно важливим сам до себе, то на головній діагоналі будуть значення, рівні 1. Надалі заповнюємо матрицю парами елементів, симетричних відносно головної діагоналі, що відображатимуть кожне твердження експерта. Використовуючи табл. 9.1 та враховуючи формулу (9.1) при перегляді тверджень експерта, отримаємо матрицю попарних порівнянь:
А = 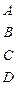
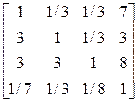 .
.
9.5.2 Приклад 2. (Побудова ієрархії МАІ).
Розглянемо ілюстративний приклад. Родині з середнім достатком необхідно придбати автомобіль. У результаті аналізу виявилися наступні критерії, які необхідно при цьому врахувати: престижність; вартість; питомі витрати пального; комфортність; надійність; максимальна швидкість; розміри; технічне обслуговування; гарантійні зобов'язання.
Необхідно побудувати ієрархію розв'язання цієї проблеми методом МАІ.
Розв'язання
Подальший розгляд дозволив обрати у якості кандидатів три моделі автомобілів та представити задачу у вигляді ієрархії (рис. 9.2).


Рисунок 9.2 – Декомпозиція задачі купівлі автомобіля в
ієрархії
У випадку прикладу первинна множина критеріїв після аналізу була звужена до наступних суттєвих: Q1 – комфортність; Q2 – надійність; Q3 – швидкість; Q4 – вартість; Q5 - престижність; Q6 –обслуговування; Q7 – гарантії; Q8 – витрати пального.
Шляхом опитування членів родини побудована наступна матриця попарних порівнянь для рівня 2 – критеріїв (табл. 9.3).
Таблиця 9.3 – Матриця попарних порівнянь критеріїв Q1- Q8 купівлі автомобіля
| Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | |
| Q1 | 1/3 | 1/4 | ||||||
| Q2 | 1/5 | 1/3 | 1/5 | 1/7 | ||||
| Q3 | 1/3 | 1/5 | ||||||
| Q4 | 1/7 | 1/5 | 1/6 | 1/3 | 1/4 | 1/7 | 1/8 | |
| Q5 | 1/6 | 1/3 | 1/3 | 1/2 | 1/5 | 1/6 | ||
| Q6 | 1/6 | 1/3 | 1/4 | 1/5 | 1/6 | |||
| Q7 | 1/6 | 1/2 | ||||||
| Q8 |
Після цього, порівнюючи попарно три автомобілі (А, В, С) за кожним з восьми критеріїв (рівень 3), отримаємо вісім матриць (для кожного з критеріїв) розміром 3х3 (за кількістю альтернатив до вибору) (табл. 9.4).
Таблиця 9.4 – Матриці попарних порівнянь альтернатив А, В, С за критеріями
| Q1 | А | В | С | Q2 | А | В | С | Q3 | А | В | С | Q4 | А | В | С |
| А | А | 1/5 | А | А | |||||||||||
| В | 1/6 | В | 1/7 | 1/8 | В | 1/8 | 1/4 | В | |||||||
| С | 1/8 | 1/4 | С | С | 1/6 | С | |||||||||
| Q5 | А | В | С | Q6 | А | В | С | Q7 | А | В | С | Q8 | А | В | С |
| А | А | А | 1/2 | 1/2 | А | 1/7 | 1/5 | ||||||||
| В | 1/5 | 1/3 | В | 1/8 | 1/5 | В | В | ||||||||
| С | 1/4 | С | 1/6 | С | С | 1/3 |
ТЕМА 10. РОЗШИРЕННЯ МЕТОДУ АНАЛІЗУ ІЄРАРХІЙ
МАІ є достатньо універсальним і за певних умов може використовуватися й для узагальнених випадків дослідження складних проблем, а саме, коли участь в опитуванні приймають не один, а декілька експертів (в цьому випадку необхідно розробити та обґрунтувати процедуру агрегації тверджень декількох експертів, щоб отримати агреговані оцінки для кожної вершини ієрархії) а також за умов, коли не всі альтернативи порівнюються чи можуть бути порівняні за всіма критеріями, чи не всі критерії можуть бути застосовані для оцінювання якості альтернатив. В останніх варіантах йдеться не про агрегування, а про методи усунення цієї додаткової невизначеності таким чином, щоб за певних припущень перетворити задачу до стандартного вигляду, що дозволяє застосування розглянутого в темі 9 алгоритму методу МАІ. Окрім того, коли переваги елементів ієрархії за тим чи іншим критерієм 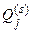 змінюються в часі, необхідно також розширити МАІ і на цей динамічний випадок. За певних припущень такі узагальнення можна зробити і успішно застосувати метод аналізу ієрархій і до нестандартних ситуацій.
змінюються в часі, необхідно також розширити МАІ і на цей динамічний випадок. За певних припущень такі узагальнення можна зробити і успішно застосувати метод аналізу ієрархій і до нестандартних ситуацій.
10.1 Динамічні переваги і пріоритети
Переваги експерта, на основі яких будувалися матриці попарних порівнянь А 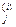 та обиралася найкраща альтернатива, є «прив’язаними» до певного моменту часу, і результати такого вибору можуть застосовуватися в майбутньому лише за умови стаціонарності середовища. В той же час в більшості випадків переваги експерта мають тенденцію до зміни в часі, тобто бажано знати, якими будуть переваги експерта в той чи інший момент часу t.
та обиралася найкраща альтернатива, є «прив’язаними» до певного моменту часу, і результати такого вибору можуть застосовуватися в майбутньому лише за умови стаціонарності середовища. В той же час в більшості випадків переваги експерта мають тенденцію до зміни в часі, тобто бажано знати, якими будуть переваги експерта в той чи інший момент часу t.
Отже, задача прогнозування експертних переваг пов’язана з одержанням оцінок пріоритетності альтернатив Bj 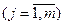 у формі залежності від часу. Оцінка переваги може бути задана не константою, а функцією, залежно від часу t. Підбір таких функцій можна здійснити, надавши в розпорядження експерта деяку функціональну шкалу, або шляхом апроксимації експертних оцінок, отриманих у різні моменти часу. Приклад функціональної шкали, де функції переваги містять параметри, підбір яких дозволяє більш-менш точно описати твердження, що змінюються, і установити область припустимих значень функції у межах дев’ятибальної шкали наведені в табл.10.1. Ці функції є такими, що в більшості випадків дозволяють достатньо точно прогнозувати зміну переваг експерта на певному проміжку часу. Достовірність таких оцінок буде достатньо високою у випадку короткочасних прогнозів зменшується зі збільшенням горизонту часу прогнозування.
у формі залежності від часу. Оцінка переваги може бути задана не константою, а функцією, залежно від часу t. Підбір таких функцій можна здійснити, надавши в розпорядження експерта деяку функціональну шкалу, або шляхом апроксимації експертних оцінок, отриманих у різні моменти часу. Приклад функціональної шкали, де функції переваги містять параметри, підбір яких дозволяє більш-менш точно описати твердження, що змінюються, і установити область припустимих значень функції у межах дев’ятибальної шкали наведені в табл.10.1. Ці функції є такими, що в більшості випадків дозволяють достатньо точно прогнозувати зміну переваг експерта на певному проміжку часу. Достовірність таких оцінок буде достатньо високою у випадку короткочасних прогнозів зменшується зі збільшенням горизонту часу прогнозування.
Ці функції (див. табл.10.1) відображають інтуїтивні представлення ОПР про зміни в тренді (тенденції розвитку): відсутні, лінійні, логарифмічні й експоненціальні, з наявністю екстремумів, коливальні і, нарешті, такі, що припускають катастрофічні зміни.
Для динамічних задач матриця парних порівнянь А містить функції часу t у якості елементів, тому максимальне власне значення λmax, а також власний вектор 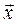 також будуть залежати від часу t, тобто
також будуть залежати від часу t, тобто
А 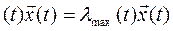 , (10.1)
, (10.1)
де А (t) – матриця парних порівнянь об’єктів, що містить інформацію про зміну переваги однієї альтернативи над іншою на деякому проміжку часу.
У випадку невеликого розміру матриці парних порівнянь А (t) (до 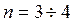 ) та простої функції переваг, що апроксимує динаміку переваг експерта, розв’язання рівняння (10.1) можна отримати в аналітичному вигляді, в більшості ж випадків розв’язання отримується за допомогою чисельних методів. Окрім того, можливе створення системи, що накопичує інформацію про реальні переваги експерта в минулих періодах та шляхом екстраполяції прогнозує їх на близьке майбутнє.
) та простої функції переваг, що апроксимує динаміку переваг експерта, розв’язання рівняння (10.1) можна отримати в аналітичному вигляді, в більшості ж випадків розв’язання отримується за допомогою чисельних методів. Окрім того, можливе створення системи, що накопичує інформацію про реальні переваги експерта в минулих періодах та шляхом екстраполяції прогнозує їх на близьке майбутнє.
Таблиця 10.1 – Функції, що апроксимують динамічні твердження
| Вид функції | Описання функції | Випадок застосування |
| const | Для всіх t: 1≤const≤9 | Сталість переваг |
| at + b | Лінійна функція від t на деякому відрізку; обернена функція – гіпербола | Лінійне зростання переваги однієї альтернативи перед іншою в часі |
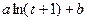
| Логарифмічне зростання | Швидке зростання переваги однієї альтернативи перед іншою до деякого t, після якого повільне зростання |
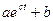
| Експоненціальний ріст (c>0) чи убування (c<0), в останньому випадку зворотна величина– S- подібна логістична крива. | Повільне збільшення чи зменшення переваги в часі, після якого надходить швидке збільшення (зменшення) |
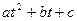
| Парабола з максимумом чи мінімумом в залежності від того, негативне чи позитивне значення приймає параметр a | Зростання до максимуму, а потім убування (чи навпаки) |
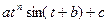
| Коливна функція | Коливання переваг у часі зі зростаючою (n>0) чи убуваючою (n<0) амплітудою |
| Катастрофи | Функції, що мають розриви, які потрібно вказати | Украй різкі зміни інтенсивності переваг |
10.2 Врахування тверджень декількох експертів
Для підвищення ступеня об’єктивності і якості процедури прийняття рішень доцільно враховувати думки декількох експертів. З цією метою проводиться групова експертиза, причому множина експертів може бути поділена на декілька множин у залежності від області експертизи, обумовлена характером критеріїв, що використовуються в ієрархії. Оцінка вагомості критеріїв Qі і альтернатив Bj з урахуванням такого підходу припускає залучення фахівців – керівників (користувачів), маркетологів, виробничників, фахівців – теоретиків, фахівців в галузях бізнес – реінженерії та консалтингу і т.п.
Агрегування тверджень експертів в багатьох випадках здійснюється за допомогою середнього геометричного, і елементи агрегованої матриці порівнянь А А =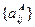 обчислюються за формулою:
обчислюються за формулою:
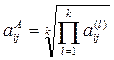
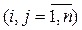 , (10.2)
, (10.2)
де k – кількість експертів. Причому
А 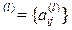 – матриця парних порівнянь l -го експерта.
– матриця парних порівнянь l -го експерта.
Логічність такого способу агрегування ґрунтується на наступному твердженні: якщо два рівноцінних експерти вказують при порівнянні об’єктів відповідно оцінки h і 1/ h, це при обчисленні агрегованої оцінки дає 1 і свідчить про еквівалентність порівнюваних об’єктів.
Усереднення тверджень експертів може бути здійснене і на рівні власних векторів 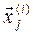 матриць парних порівнянь А
матриць парних порівнянь А 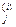 . При цьому результати будуть еквівалентні тим, що отримані на рівні елементів матриць (10.2), якщо однорідність складених матриць достатня і відповідає умові I0 < 0,1 (I0% < 10%).
. При цьому результати будуть еквівалентні тим, що отримані на рівні елементів матриць (10.2), якщо однорідність складених матриць достатня і відповідає умові I0 < 0,1 (I0% < 10%).
В багатьох випадках існує необхідність зважування тверджень та оцінок експертів з метою врахування їх кваліфікації. У цьому випадку і для отримання обґрунтованих ваг експертів можна застосувати МАІ на ґрунті побудови ієрархічної системи критеріїв оцінювання кваліфікації експертів (рис. 10.1).
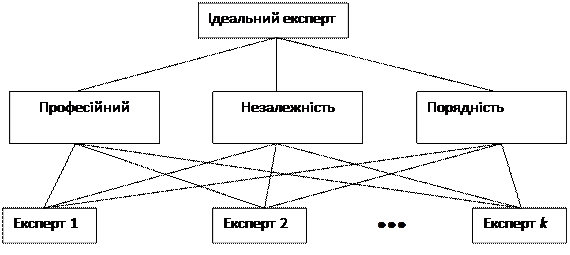 |
Рисунок 10.1 – Приклад ієрархії для оцінювання ваги експертів
У випадку, коли ваги експертів розраховані і різні, агрегування здійснюється за допомогою співвідношення:
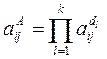
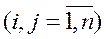 , (10.3)
, (10.3)
де k – кількість експертів; dl > 0 – „вага” l -го експерта 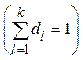 .
.
10.3 Порівняння об’єктів зі стандартами
Модифікацією МАІ є метод порівняння об’єктів зі стандартами, який виник у результаті наявності певних обмежень методу попарного порівняння альтернатив. Метод попарного порівняння альтернатив Bj 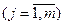 не може бути ефективно застосований у деяких практичних ситуаціях: експерту може бути запропоновано для аналізу більше, ніж дев’ять альтернатив; при надходженні нових альтернатив може змінюватися порядок, встановлений на множині вже порівняних альтернатив; альтернативи можуть надходити експерту для порівняння не одночасно, а через певні проміжки часу, і в такій ситуації неможливо попарно порівняти всі об’єкти.
не може бути ефективно застосований у деяких практичних ситуаціях: експерту може бути запропоновано для аналізу більше, ніж дев’ять альтернатив; при надходженні нових альтернатив може змінюватися порядок, встановлений на множині вже порівняних альтернатив; альтернативи можуть надходити експерту для порівняння не одночасно, а через певні проміжки часу, і в такій ситуації неможливо попарно порівняти всі об’єкти.
Для розв’язання проблеми порівняння й оцінювання альтернатив у зазначених ситуаціях застосовується метод порівняння альтернатив зі стандартами. Стандарт установлює рівень якості об’єкта щодо критерію якості. Кожен стандарт (H – high, M – medium, L – little і т.п.) ототожнюється зазвичай з деяким існуючими на практиці еталоном якості. Як такі еталони, приймаються об’єкти, аналогічні до альтернатив, що порівнюються. Наприклад, для видів забезпечення банківських кредитів високий, середній та низький стандарти за критерієм „ліквідність” можуть бути ототожнені відповідно з дорогоцінними металами, цінними паперами та нерухомістю.
В ієрархічній структурі стандарти присвоюються елементам (критеріям), що мають безпосередній зв’язок з альтернативами. При цьому число стандартів для кожного такого елементу (критерію якості) може бути різним і визначається експертом з урахуванням конкретної ситуації. Для кожного стандарту експертом установлюється відносний ступінь переваги, що відображає значимість стандарту для експерта. Чисельне значення кожного стандарту визначається їхнім попарним порівнянням за дев’ятибальною шкалою та визначенням вектору пріоритетів шляхом опрацювання відповідної матриці попарних порівнянь.
Розглянемо правила побудови ієрархії (рис. 10.2), що враховує стандарти й алгоритм обчислення векторів пріоритетів альтернатив.
Вважатимемо, що 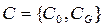 - множина стандартів, причому С0={H, M, L} – шкала основних та CG={HH, HM, ML, LL} – шкала проміжних значень (H, M, L – відповідно високий, середній і низький рівень стандартів за визначеним критерієм; HH, HM, ML, LL – відповідно дуже високе, проміжне між високим і середнім, проміжне між середнім і низьким; дуже низьке значення стандартів). Отже, у повному вигляді шкала стандартів буде мати 7 значень.
- множина стандартів, причому С0={H, M, L} – шкала основних та CG={HH, HM, ML, LL} – шкала проміжних значень (H, M, L – відповідно високий, середній і низький рівень стандартів за визначеним критерієм; HH, HM, ML, LL – відповідно дуже високе, проміжне між високим і середнім, проміжне між середнім і низьким; дуже низьке значення стандартів). Отже, у повному вигляді шкала стандартів буде мати 7 значень.
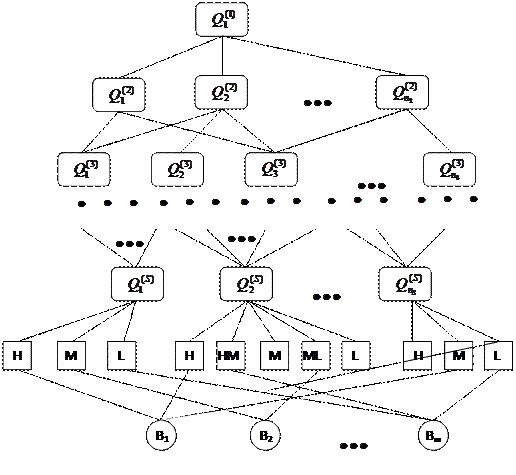 |
Рисунок 10.2 – Вигляд ієрархії з врахуванням стандартів
Для конкретного елемента ієрархії 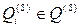 визначається підмножина стандартів
визначається підмножина стандартів 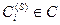
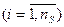 . Так, для елементів ієрархії на рис.10.2
. Так, для елементів ієрархії на рис.10.2 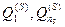 визначені стандарти H, M, L, а для елемента
визначені стандарти H, M, L, а для елемента 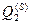 - стандарти H, HM, M, ML, L. Слід зазначити, що експертом можуть бути призначені різні значення для тих самих за найменуванням стандартів, що стосуються відповідно елементів
- стандарти H, HM, M, ML, L. Слід зазначити, що експертом можуть бути призначені різні значення для тих самих за найменуванням стандартів, що стосуються відповідно елементів 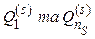 .
.
Обчислення векторів пріоритетів альтернатив 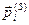
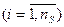 щодо елементів ієрархії, що враховує стандарти, здійснюється в такий спосіб.
щодо елементів ієрархії, що враховує стандарти, здійснюється в такий спосіб.
1. Для кожного елемента 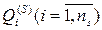 ієрархії, безпосередньо зв’язаного зі стандартами, визначається підмножина стандартів
ієрархії, безпосередньо зв’язаного зі стандартами, визначається підмножина стандартів 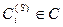 . Стандарти, що є елементами підмножини
. Стандарти, що є елементами підмножини 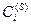 , сформовані відносно
, сформовані відносно 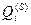 , порівнюються попарно за дев’ятибальною шкалою переваг (див. табл.9.1). Відносні переваги стандартів фіксуються в квадратних матрицях попарних порівнянь стандартів C
, порівнюються попарно за дев’ятибальною шкалою переваг (див. табл.9.1). Відносні переваги стандартів фіксуються в квадратних матрицях попарних порівнянь стандартів C 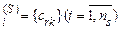 , опрацювання яких за формулами виду (9.3) дозволяє визначити для них головні власні вектори
, опрацювання яких за формулами виду (9.3) дозволяє визначити для них головні власні вектори 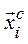 , що відображають пріоритети стандартів відносно критеріїв
, що відображають пріоритети стандартів відносно критеріїв 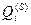 нижнього рівня ієрархії, з якими вони пов’язані безпосередньо, і є числовими оцінками значень стандартів для кожного з вказаних вище критеріїв
нижнього рівня ієрархії, з якими вони пов’язані безпосередньо, і є числовими оцінками значень стандартів для кожного з вказаних вище критеріїв  (див. рис.10.2). У власному векторі
(див. рис.10.2). У власному векторі 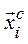 верхній індекс „c” вказує на належність вектора рівню стандартів в ієрархії.
верхній індекс „c” вказує на належність вектора рівню стандартів в ієрархії.
2. ОПР присвоює кожній альтернативі Bj 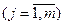 значення одного стандарту для кожного з елементів (критеріїв)
значення одного стандарту для кожного з елементів (критеріїв) 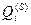 , що безпосередньо пов’язані зі стандартами, виміряними у відповідній шкалі (множині)
, що безпосередньо пов’язані зі стандартами, виміряними у відповідній шкалі (множині) 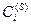 елемента
елемента 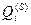 . В результаті чого будується агрегована матриця стандартів А С:
. В результаті чого будується агрегована матриця стандартів А С:

 А С =
А С = 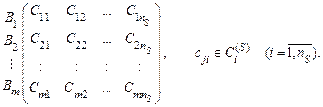 (10.4)
(10.4)
3. Після цього матриця А С перетворюється до числового вигляду з використанням векторів 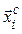
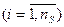 : кожному значенню
: кожному значенню 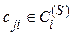 відповідає значення однієї і лише однієї компоненти вектора
відповідає значення однієї і лише однієї компоненти вектора 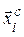 . В результаті отримуємо
. В результаті отримуємо 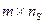 ненормалізовану матрицю U числових значень стандартів, що відповідають альтернативам Bj та елементам ієрархії
ненормалізовану матрицю U числових значень стандартів, що відповідають альтернативам Bj та елементам ієрархії 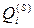 , безпосередньо пов’язаними зі стандартами. На основі матриці U формуємо нормуючу матрицю S та здійснюємо нормування матриці U за формулою:
, безпосередньо пов’язаними зі стандартами. На основі матриці U формуємо нормуючу матрицю S та здійснюємо нормування матриці U за формулою:
U N = U 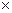 S -1, (10.5)
S -1, (10.5)
де
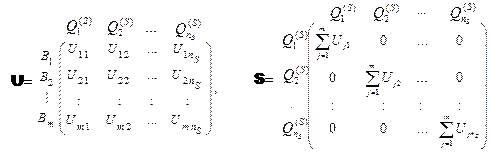 |
(10.6)
4. В результаті стовпчики матриці U N = U 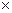 S -1 будуть нічим іншим, як векторами пріоритетів альтернатив
S -1 будуть нічим іншим, як векторами пріоритетів альтернатив 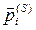
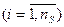 відносно елементів
відносно елементів 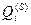 ієрархії:
ієрархії:
U N 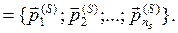
5. Отже, ми реалізували крок 1 алгоритму синтезу пріоритетів альтернатив, що враховує стандарти. Надалі алгоритм працює згідно викладеної в методі МАІ послідовності кроків без змін (див. підрозд.9.4).
10.4 Порівняння об’єктів методом копіювання
Метод копіювання застосовується в тих випадках, коли серед альтернатив Bj 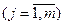 наявні такі, котрі мають одну або декілька ідентичних властивостей (значень критерію (- їв) якості). Нехай наявна множина альтернатив B={Br}, тобто
наявні такі, котрі мають одну або декілька ідентичних властивостей (значень критерію (- їв) якості). Нехай наявна множина альтернатив B={Br}, тобто 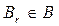
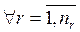 , кожна з яких відрізняється від інших за значенням певного критерію
, кожна з яких відрізняється від інших за значенням певного критерію 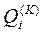 , а також множина альтернатив
, а також множина альтернатив 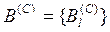 , тобто
, тобто 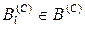
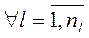 , значення яких за критерієм
, значення яких за критерієм 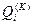 рівні між собою для всіх альтернатив множини
рівні між собою для всіх альтернатив множини 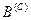 , і крім того, дорівнюють значенню за цим критерієм альтернативі
, і крім того, дорівнюють значенню за цим критерієм альтернативі 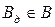 (див. рис.9.1). У цьому випадку множину альтернатив
(див. рис.9.1). У цьому випадку множину альтернатив 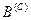 можна розглядати як копії альтернативи
можна розглядати як копії альтернативи 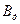 за критерієм
за критерієм 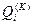 .
.
При застосуванні методу копіювання експерт порівнює між собою за критерієм 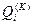 методом парних порівнянь лише альтернативи множини В з наступним розрахунком нормованого власного вектора матриці парних порівнянь
методом парних порівнянь лише альтернативи множини В з наступним розрахунком нормованого власного вектора матриці парних порівнянь 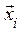 , що забезпечує ранжування альтернатив. Всі альтернативи множини
, що забезпечує ранжування альтернатив. Всі альтернативи множини 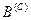 отримують те ж значення, що дорівнює значенню компоненти власного вектора
отримують те ж значення, що дорівнює значенню компоненти власного вектора 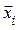 для альтернативи
для альтернативи 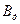 . Загальна множина альтернатив
. Загальна множина альтернатив 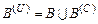 , і новий ненормований вектор пріоритетів альтернатив для множини
, і новий ненормований вектор пріоритетів альтернатив для множини  матиме вигляд:
матиме вигляд:
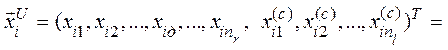
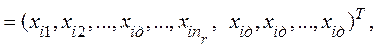
і переіндексовуючи компоненти отримуємо:
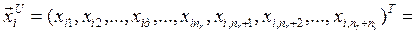
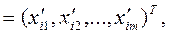 (10.7)
(10.7)
де m = nr + nl – загальна кількість альтернатив 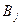 в ієрархії.
в ієрархії.
Після цього виконуємо нормування:
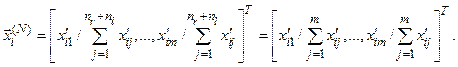 (10.8)
(10.8)
Як і метод порівняння об’єктів зі стандартами (див. підрозд.10.3), метод копіювання також не порушує порядок раніше проранжованих альтернатив при додаванні нових, що є копіями раніше проранжованих. Крім того, число альтернатив при додаванні копій може перевищувати граничне значення рівне дев’яти для методу МАІ попарного порівняння.
Метод копіювання дозволяє істотно скоротити час експертів на підготовку вихідних даних для аналізу і зменшити ймовірність внесення в них як випадкових, так і логічних помилок.
10.5 Багатокритеріальний вибір на ієрархіях з різним числом і складом критеріїв оцінювання альтернатив
У практиці прийняття рішень зустрічається також задача, коли альтернативи Bj 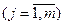 , що можуть бути оцінені за певною множиною критеріїв, з тих чи інших причин оцінюються експертом не за всіма критеріями. Ця задача характерна для ситуацій, у яких множина критеріїв є надлишковою що до однієї чи декількох альтернатив. У випадку ієрархії (рис.10.3) експерт має різну кількість альтернатив під кожним (чи під частиною) критеріїв.
, що можуть бути оцінені за певною множиною критеріїв, з тих чи інших причин оцінюються експертом не за всіма критеріями. Ця задача характерна для ситуацій, у яких множина критеріїв є надлишковою що до однієї чи декількох альтернатив. У випадку ієрархії (рис.10.3) експерт має різну кількість альтернатив під кожним (чи під частиною) критеріїв.
Зрозуміло, що у цьому випадку різні альтернативи оцінюються за різною кількістю критеріїв, і існує принципова невизначеність в тому, яким чином враховувати цю ситуацію. Розглянемо алгоритм визначення вектора пріоритету альтернатив 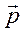 для випадку, коли ієрархія має один рівень критеріїв, об’єднаних фокусом (див. рис.10.3) з урахуванням значимості критеріїв, і різної кількості альтернатив у кожного критерію
для випадку, коли ієрархія має один рівень критеріїв, об’єднаних фокусом (див. рис.10.3) з урахуванням значимості критеріїв, і різної кількості альтернатив у кожного критерію 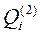
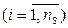 .
.
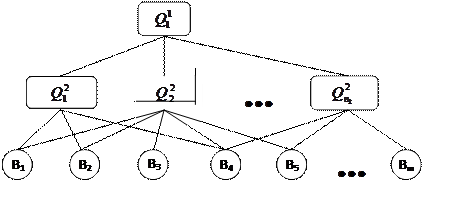 |

Рисунок 10.3 – Ієрархія з різним складом критеріїв оцінювання
альтернатив
Алгоритм побудови вектора пріоритету альтернатив при оцінюванні їх різною кількістю критеріїв:
Крок 1. Первісна проблема структурується у виді ієрархії Q={Q1,Q2,…,Qn} – передостанній рівень ієрархічної структури, та альтернатив B={B1,B2,…,Bm} – останній рівень ієрархічної структури (рівень листя).
Крок 2. На основі ієрархічної структури проблеми що розглядається, визначається бінарна матриця Н
Н = { hij }, hij 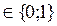
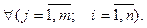 (10.9)
(10.9)
Якщо альтернатива Bj оцінюється за критерієм Qi, то hij = 1, якщо ні, то hij = 0.
Крок 3. Здійснюється експертна оцінка альтернатив Bj 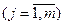 за відповідними критеріями, використовуючи метод МАІ попарного порівняння (можуть також використовуватися розширення МАІ – порівняння за стандартами (див. підрозд.10.3) чи метод копіювання (див. підрозд.10.4)). На основі матриці парних порівнянь альтернатив А i
за відповідними критеріями, використовуючи метод МАІ попарного порівняння (можуть також використовуватися розширення МАІ – порівняння за стандартами (див. підрозд.10.3) чи метод копіювання (див. підрозд.10.4)). На основі матриці парних порівнянь альтернатив А i 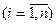 за критеріями Qi будується матриця головних власних векторів А, стовпці якої є векторами пріоритетів альтернатив
за критеріями Qi будується матриця головних власних векторів А, стовпці якої є векторами пріоритетів альтернатив 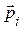
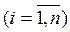 відносно критеріїв, тобто
відносно критеріїв, тобто
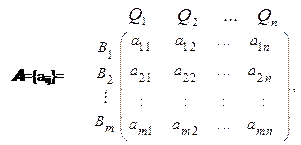
(10.10)
де 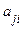 = 0, якщо альтернатива Bj не оцінюється за критерієм Qi. Вектори (стовпці) в матриці А мають різне число ненульових (
= 0, якщо альтернатива Bj не оцінюється за критерієм Qi. Вектори (стовпці) в матриці А мають різне число ненульових (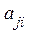
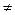 0) значень, можуть бути нормованими чи ненормованими в залежності від використаного методу порівняння альтернатив.
0) значень, можуть бути нормованими чи ненормованими в залежності від використаного методу порівняння альтернатив.
Крок 4. Формується матриця парних порівнянь критеріїв А (Q), та розраховується нормований вектор пріоритетів критеріїв 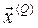 .
.
Крок 5. Формується нормуюча 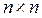 матриця S для матриці векторів пріоритетів альтернатив А (10.10) та
матриця S для матриці векторів пріоритетів альтернатив А (10.10) та 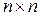 матриця структурного критерію L за зразком:
матриця структурного критерію L за зразком:
 |
(10.11)
де ri 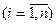 - число альтернатив множини В, що порівнюється за критерієм Qi;
- число альтернатив множини В, що порівнюється за критерієм Qi; 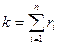 - загальна кількість альтернатив, що порівнюються за всіма критеріями
- загальна кількість альтернатив, що порівнюються за всіма критеріями 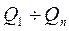 .
.
Використання структурного критерію L дозволяє експерту змінювати при необхідності вагу альтернатив, пов’язаних з відповідними критеріями.
Крок 6. Визначається вектор 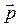 пріоритетів альтернатив Bj
пріоритетів альтернатив Bj 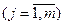 відносно критерію-фокусу
відносно критерію-фокусу 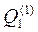 (див. рис.10.3):
(див. рис.10.3):
а) для випадку, коли матриця А (10.10) ненормована:
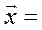 A
A 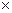 S
S 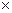 L
L 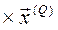 ;
; 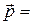 B
B 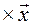 , (10.12)
, (10.12)
де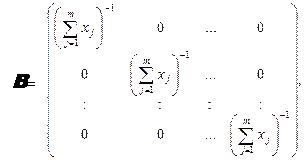
(10.13)
-  діагональна матриця, призначена для остаточного нормування значень вектора пріоритетів альтернатив;
діагональна матриця, призначена для остаточного нормування значень вектора пріоритетів альтернатив;
б) для випадку, коли матриця А (10.10) нормована:
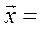 A
A 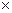 L
L 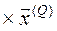 ;
; 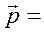 B
B 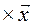 , (10.14)
, (10.14)
де матриця В формується у вигляді (10.13).
Стоп. Закінчення алгоритму.
Використання структурного критерію L змінює вагу альтернатив Bj, пов’язаних з відповідними критеріями Qi, пропорційно до відношення ri/k, чим забезпечується підвищення пріоритету альтернатив, що утворюють великі групи, і зниження пріоритету альтернатив у групах з їх відносно невеликим числом (група утворюється альтернативами, що порівнюються за певним критерієм). Можливість застосування структурного критерію L обумовлена тим, що в критеріїв-предків з високим пріоритетом в ієрархії припускається наявність великого числа альтернатив-нащадків, а в критеріїв-предків з низьким пріоритетом - значно менше число альтернатив-нащадків. В такій ситуації бажане підвищення пріоритетів альтернатив у великій групі, оскільки, якщо альтернатив багато, кожна з них одержить менший складений пріоритет, ніж кожна альтернатива, що входить у меншу групу з низьким пріоритетом критерію.
У протилежному випадку, коли потрібно підвищити пріоритет рідких альтернатив-нащадків, що утворюють щодо критеріїв-предків маленькі групи, доцільно розраховувати значення діагональних елементів матриці L за формулою 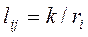
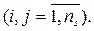 Спосіб формування структурного критерію може бути і іншим, довільним, і це є головною проблемою в обґрунтуванні такого підходу.
Спосіб формування структурного критерію може бути і іншим, довільним, і це є головною проблемою в обґрунтуванні такого підходу.
ТЕМА 11. ІНШІ МЕТОДИ СИСТЕМНОГО АНАЛІЗУ
11.1 Методи дерева цілей, функціонального аналізу та формування ё
експертних висновків
Метод дерева цілей – орієнтований на одержання повної і відносно стійкої структури цілей, проблем, функцій, напрямків, тобто такої структури, яка мало змінюватиметься протягом певного періоду часу при неминучих змінах, що відбуваються в будь-якій системі, яка розвивається. Для досягнення цього при побудові варіантів структури варто враховувати закономірності цілеутворення, і використовувати принципи і методики формування ієрархічних структур цілей і функцій. Структурування дає можливість деталізувати цілі і шляхи їхнього досягнення, виявити існуючі між ними взаємозв’язки, забезпечити визначену логіку розв’язання проблеми. Структуру дерева цілей доцільно формувати шляхом уявлення його у вигляді піраміди з послідовним обходженням всіх її граней, повертаючись на новому витку до вже структурованих раніше гілок з врахуванням нового бачення проблеми, а також використовувати загальні ознаки структурування для різних рівнів системи.
Розкриваючи одну й ту ж глобальну мету, різні аналітики можуть отримати різні ієрархічні структури, і це є природним, оскільки системний аналіз гарантується не лише на формальних процедурах та прийомах, але й на використанні інтуїції та досвіду фахівців. З іншого боку, рекомендації кваліфікованих системних аналітиків будуть близькими між собою. Особливий клас методів, що пов’язані безпосередньо з опитуванням експертів, утворюють методи експертних оцінок.
Методи експертних оцінок – широко використовуються в системному аналізі при необхідності одержання інформації про складну проблему, що характеризується великим ступнем невизначеності. Експертні оцінки - це певна „суспільна точка зору”, що залежить від рівня науково-технічних знань суспільства щодо предмета дослідження і може змінюватися під час розвитку системи і наших уявлень про неї. Експертне опитування в більшості випадків не є одноразовою процедурою, воно повинне бути вбудованим у складну систему, тобто необхідно створити регулярну систему роботи з експертами. Метод Дельфі (чи „дельфійського оракула”) був розроблений для розв’язання складних стратегічних проблем з метою отримання інформації про майбутнє, гранично зменшити вплив суб’єктивного фактору, стимулювати способи мислення спеціалістів шляхом створення інформаційної системи з оберненими зв’язками, усунути завади в обміні інформацією між фахівцями, тиск авторитету та інші форми тиску, забезпечити підвищення достовірності прогнозів шляхом спеціальних процедур кількісного оцінювання думок експертів та їх опрацювання. Анонімність та можливість поповнити інформацію про предмет експертизи створюють умови, що забезпечують найбільш продуктивну працю експертної комісії. Крім того, наявність зворотного зв’язку, що реалізується в декілька турів, дозволяє експертам корегувати свої висловлювання з врахуванням проміжних усереднених оцінок та пояснень експертів, які висловили полярні точки зору.
Для того, щоб знизити витрати, врахувати в більшій мірі побажання споживачів, і скоротити терміни розроблення і виходу на ринок продукції, застосовують наступні технології розроблення нових й аналізу розроблених виробів і процесів:
· функціонально-вартісний аналіз (ФВА);
· технологію аналізу, можливості виникнення і впливи дефектів на споживача - FMEA;
· функціонально-фізичний аналіз (ФФА);
· технологію розгортання функцій якості - QFD.
Метою функціонально-фізичного аналізу (ФФА) – є аналіз фізичних принципів дії, технічних і фізичних суперечностей у технічних об’єктах (ТО) для того, щоб оцінити якість прийнятих технічних рішень і запропонувати нові технічні рішення.
При застосуванні методу мозкової атаки – реалізується процес колективної генерації ідей, забезпечується якнайбільша свобода мислення учасникам і висловлення ними нових ідей, що сприяє виявленню нетривіальних шляхів розв’язання складних проблем. У методі сценаріїв побудова сценарію дозволяє створити попереднє представлення про проблему (систему) у ситуаціях, коли не вдається відразу відобразити її за допомогою формальної моделі.
Метод комісії – полягає в організації та проведенні відкритої дискусії з метою отримання єдиного узгодженого висновку експертів, причому висновок визначається шляхом відкритого або таємного голосування. Ділові ігри дозволяють за допомогою моделювання й імітації процесів вийти на аналіз, розв’язання складних практичних задач, забезпечити формування розумової культури, керування, майстерності спілкування, прийняття рішень, інструментальне розширення управлінських навичок, є по суті засобом аналізу систем керування і підготовки фахівців.
(Більш детальне вивчення питання виноситься на самостійну проробку).
11.2 Методи комбінаторно-морфологічного аналізу і синтезу
Морфологія – це структурна форма системи, організована відповідно до її функцій. Фактично морфологічний аналіз є методом розвитку творчих здібностей, або, точніше, систематичним допоміжним засобом для творчості. Він зовсім не виключає творчої праці людини, а стимулює її, і розширює її можливості, поширюючи на більше число ідей, ніж це було б можливим при класичному підході. Основна ідея морфологічного підходу полягає в тому. Щоб знаходити найбільшу кількість, а гранично й всі можливі шляхи розв’язання поставленої проблеми шляхом комбінування основних структурних елементів систем або ознак рішень. У цьому випадку система або проблема може бути піддана декомпозиції різними способами і розглядатися в різних аспектах.
Метод морфологічного дослідження реалізується в два якісно різних етапи.
Перший етап – полягає в одержанні описів всіх систем, що належать до досліджуваного класу, тобто є класифікацією множини систем - морфологічним аналізом.
На етапі морфологічного синтезу – проводяться оцінювання описів різних систем класу, що досліджується, і вибір тих, які у тому або іншому наближенні відповідають умовам задачі. Отримується цілісний опис усієї досліджуваної системи на рівні описів окремих підсистем і відношень між ними.
Формування первісної мети синтезу може здійснюватися з різним ступенем повноти та визначеності і значною мірою визначає підходи з формування пошукових завдань і морфологічних таблиць. Пошукові завдання формуються: на ґрунті якісних класифікаційних ознак і їхніх значень, що характеризують окремі підсистеми варіанта системи; на ґрунті кількісної експертної шкали у вигляді деякої кількості критеріїв якості і необхідного рівня їхнього досягнення в рішенні, що шукається.
Морфологічні таблиці – дозволяють систематизувати досить великий обсяг знань про морфологію систем у компактному вигляді і розробляються на етапі морфологічного аналізу. На підставі функціонально-елементарного аналізу формуються рядки морфологічної таблиці, у які записуються функції системи або узагальнені функціональні підсистеми, з яких складається система загалом. Рядки морфологічної таблиці визначаються з функцій або узагальнених функціональних підсистем, що належать до одного ієрархічного рівня. Найменуваннями стовпців є альтернативи-варіанти реалізації функцій. Після формування класифікацій здійснюється опис альтернатив кожної функції відповідними ознаками і значеннями цих ознак, тобто складаються класифікаційні образи альтернатив, а опрацювання таких морфологічних таблиць реалізується методами кластерного аналізу.
Морфологічний синтез – раціональних варіантів за критеріями якості починається із незалежної оцінки альтернатив, що належать відповідним функціональним підсистемам. Кількість елементів первісної морфологічної множини попередньо зменшується шляхом відсічення нераціональних варіантів. Підмножина раціональних варіантів яка залишилася після відсічення, досліджується на предмет їх ефективності та сумісності окремих альтернатив. Для повнішого аналізу множин досліджуваних об’єктів можуть розрахуватися мірі подібності, відмінності та включення для всіх пар об’єктів, а для визначення кількості класів та класифікацій - алгоритми кластерного аналізу. Функціональні підсистеми, із котрих складається деяка функціональна система, можуть вносити різний внесок у її ефективність та новизну, а тому у таких випадках необхідно оцінювати відносний внесок функціональних підсистем.
Відмінною особливістю морфологічних методів деревовидного, лабіринтного та блочно-лабіринтного синтезу раціональних варіантів систем – є те, що у них оцінка міри відповідності синтезованого варіанта початковій меті синтезу здійснюється безпосередньо під час процедури побудови варіанта, що шукається, по мірі нарощування функціональних підсистем. Використання цих методів найвиправданіше для багатофункціональних складних організаційних та соціально-економічних систем і дозволяє суттєво зменшити число операцій вибору у порівнянні із повним перебором варіантів, що містяться у морфологічній таблиці.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 7459; Нарушение авторских прав?; Мы поможем в написании вашей работы!