Зображення процесів на фазовій площині

Якщо рівняння системи представлені у нормальній формі, то вектор стану системи однозначно визначає її стан. Кожному стану системи в просторі станів відповідає точка. Точка, яка відповідає поточному стану системи називається зображуючою точкою. При зміні стану зображуюча точка описує траекторію. Ця траекторія називається фазовою траекторією. Сукупність фазових траекторій, яка відповідає різним можливим початковим умовам, називається фазовим портретом.

Наочно фазову траекторію та фазовий портрет можна представити у випадку двомірного фазового простору. Двомірний фазовий простір називається фазовою площиною.

Фазова площина – це координатна площина, в якій по осях координат відкладаються дві змінні (фазові координати), які однозначно визначають стан системи другого порядку. Метод аналізу та синтезу системи управління, який базується на побудові фазового портрета, називається методом фазової площини.

Через будь-яку точку фазового простору може проходити лише одна траекторія. Однак, на фазовій площині існують особливі точки – точки в яких фазова швидкість рівна нулю, а отже це точки які є положенням рівноваги системи. Через особливі точки може проходити більше одної фазової траекторії.

Часто при зображенні процесів на фазовій площині за фазову координату 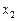, яку відкладають по осі ординат, приймають похідну координати , що відкладається по осі абсцис. В цьому випадку диференціальне рівняння фазових траекторій матиме вигляд:

.

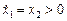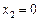Тоді фазові траекторії матимуть наступні властивості. У верхній півплощині зображуюча точка рухається зліва направо, оскільки та зростає. В нижній півплощині, навпаки, зображуюча точка рухається справа наліво так як та спадає. На осі абсцис () похідна 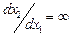(за винятком точок рівноваги), і тому фазові траекторії перетинають вісь абсцис під прямим кутом.

Фазові портрети нелінійних систем характеризуються більшим різномаїттям, ніж фазові портрети лінійних систем. Однак типи особливих точок лінійних та нелінійних систем співпадають. Тут маються на увазі ті особливі точки, в околі яких рівняння нелінійних систем допускають лінеаризацію.

Фазові портрети та типи особливих точок лінійних систем. Нехай лінійна система другого порядку описується рівнянням

,

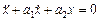або в нормальній формі,

. (*)

Розв’язок, фазовий портрет та типи особливих точок залежать від коренів характеристичного рівняння

.

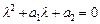З рівняння (*) випливає, що система що розглядається має одну особливу точку в початку координат. В залежності від вигляду фазового портрету в околі особливих точок, останні поділяються на різні типи.

В табл. 1.2 наведені часові характеристики, фазові портрети та типи особливих точок при різних коренях характеристичного рівняння.

Таблиця 1.2

Тип коренів	Крива перехідного процесу	Фазовий портрет	Тип особливої точки
Чисто уявні			Центр
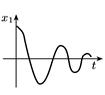
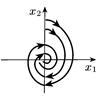
Комплексні з від’ємною дійсною частиною			Стійкий фокус
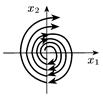
Комплексні з додатньою дійсною частиною			Нестійкий фокус
Дійсні від’ємні			Стійкий вузол
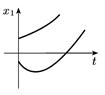
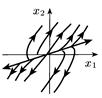
Дійсні додатні			Нестійкий вузол
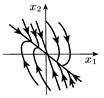
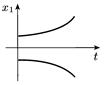
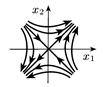
Дійсні різних знаків			Сідло

Коли корені характеристичного рівняння є чисто уявними,фазові траекторії є еліпсами або колами, тобто вони є замкнутими.

Замкнутим фазовим траекторіям відповідають незатухаючі коливання. Однак ці коливання не є автоколиваннями, так як їх амплітуда залежить від початкових умов і вони не є асимптотично орбітально стійкими.

Фазові портрети нелінійних систем. Нелінійні системи можуть мати декілька положень рівноваги (особливих точок) і характеризуються більшим різномаїттям фазових портретів. Якщо праві частини нелінійних рівнянь допускають лінеаризацію в околі особливих точок, то ці особливі точки можуть бути лише тих самих типів, що й особливі точки у випадку лінійних систем.

При наявності декількох точок рівноваги можливі різні типи фазових траекторій. Особливі криві, що розділяють фазову площину на області з різними типами фазових траекторій, називаються сепаратрисами.

Фазові портрети нелінійних систем можуть мати інший тип особливої кривої – ізольовані замкнуті траекторії. Ці криві називаються граничними циклами. Якщо зсередини та зовні фазові траекторії сходяться до граничного циклу (рис. 1.3*,а), то такий граничний цикл називається стійким граничним циклом. Стійкому граничному циклу відповідає асимптотично орбітально стійкий періодичний рух (автоколивання). В системі, у якої фазовий портрет має вигляд, представлений на рис. 1.3*,а, автоколивання виникають самовільно при будь-яких початкових умовах.

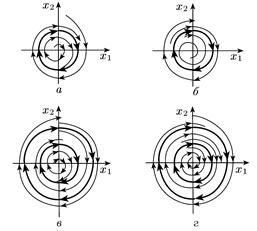
Рис. 1.3*. Граничні цикли

Якщо фазові траекторії зсередини та зовні граничного цикла віддаляються від нього (рис. 1.3*,б), такий граничний цикл називається нестійким граничним циклом. Періодичний процес що відповідає нестійкому граничному циклу неможливо спостерігати. Якщо рух починається всередині такого граничного цикла, то процес зходиться до положення рівноваги. Якщо рухпочинається зовні такого граничного циклу, то процес розходиться. Нестійкий граничний цикл є границею області притягання, або границею стійкості положення рівноваги (початку координат).

Можливі два граничні цикли (рис. 1.3*,в,г). Внутрішній граничний цикл на рис. 1.3*,в стійкий, і йому відповідають автоколивання, а зовнішній граничний цикл нестійкий і є границею області автоколивань: автоколивання виникають при будь-яких початкових відхиленнях, що не виходять за зовнішній граничний цикл.

Зовнішній граничний цикл на рис. 1.3*,г є стійким і відповідає автоколиванням, а внутрішній граничний цикл є нестійким і є границею області притягання положення рівноваги. В системі з таким фазовим портретом автоколивання виникають при досить значному відхиленні системи від положення рівноваги – відхиленні, яке виходить за межі внутрішнього граничного цикла. Якщо рух системи починається всередині нестійкого граничного цикла, то вона наближається до положення рівноваги.

Дата добавления: 2014-01-07