Корекція цифрових систем

Раніше розглядалися основні поняття про корекцію імпульсних систем, для здійснення якої є більш широкі можливості порівняно з безперервними САК, оскільки коректувальні пристрої можуть бути безперервними або дискретними.

Одним з шляхів підвищення якості процесу керування ЦС є застосування цифрових коректуючих пристроїв або цифрових коректуючих фільтрів. Ці фільтри можуть бути диференційними та інтегруючими.

Диференційний фільтр першого порядку реалізує різницеве рівняння:

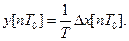(3.68)

Це відповідає наближеному різницевому виразу похідної від вхідної величини. Передаточна функція диференціювального фільтра першого порядку:

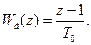(3.69)

Для практичної реалізації цю функцію перетворюють до вигляду:

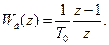(3.70)

Для більш точної реалізації похідної від вхідної величини передаточну функцію подають у такому вигляді:

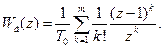(3.71)

де m – скінчена кількість членів суми, що вибирається з бажаної точності реалізації похідної.

Аналогічно будується диференційний цифровий фільтр будь-якого порядку r з передаточною функцією:

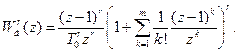(3.72)

Такі фільтри дають суттєвий ефект як при послідовному включенні, так і в місцевих зворотних зв’язках. Вони також дозволяють забезпечувати інваріантність за зовнішнім вхідним впливом.

Інтегруючий цифровий фільтр першого порядку імітує інтеграл у вигляді наближеної рівності:

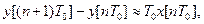(3.73)

що відповідає наближеному інтегруванню за методом прямокутників.

Передаточна функція такого фільтра має вигляд:

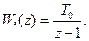(3.74)

Оскільки розв’язок різницевого рівняння (3.73) дає:

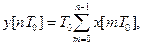(3.75)

то такий фільтр називають накопичувачем.

Існує також інший вираз передаточної функції інтегруючого фільтра першого порядку, який відповідає інтегруванню за методом трапецій:

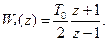(3.76)

Для цифрового інтегруючого фільтра другого порядку (при інтегруванні за правилом Симпсона) передаточна функція має вигляд:

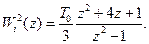(3.77)

Послідовне включення інтегруючого фільтра підвищує порядок астатизму системи, тобто її точність. Однак, як і для безперервних систем, при цьому можливе погіршення стійкості системи. Тому застосовують ізодромну корекцію. Передаточна функція у цьому разі має вигляд:

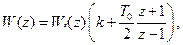(3.78)

де передаточна функція 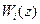відповідає (3.74) або (3.76), а значення k дорівнює сталій часу компенсуючого диференціювального пристрою першого порядку.

Існують ще цифрові фільтри іншого типу, які забезпечують бажані показники якості процесів керування в ЦС при тих чи інших зовнішніх впливах.

Дата добавления: 2014-01-07