Синтез цифрових коректуючих пристроїв методом ЛАЧХ

Під час розробки цифрових систем керування зручно використовувати метод синтезу, що базується на логарифмічних частотних характеристиках. Передаточна функція розімкнутої ЦС є добутком дискретних передаточних функцій приведеної безперервної частини і цифрового регулятора: 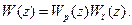Якщо перейти до логарифмічних характеристик, як функцій абсолютної псевдочастоти l, то можна записати:

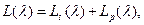(3.79)

де 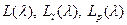- амплітудні логарифмічні характеристики розімкнутої системи, приведеної безперервної частини і цифрового регулятора.

Звідси ЛАЧХ цифрового регулятора:

(3.80)

Як зауважувалось раніше за умови wТ₀ < 2 псевдочастоту l можна замінити дійсною частотою w, тому для низьких частот (w < 2/Т₀) побудова ЛАЧХ і ЛФЧХ дискретної системи зводиться по суті до побудови відповідних характеристик початкової (не приведеної) безперервної частини системи з передаточною функцією

Розглянемо побудову логарифмічних характеристик у зоні високих частот (при w > 2/Т₀). Якщо сталі часу передаточної функції 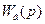такі, що всі частоти спряження асимптотичної ЛАЧХ лежать ліворуч від частоти w = 2/Т₀ і ЛАЧХ при цій частоті має нахил (-20×n) дБ/дек, то високочастотна частина ЛАЧХ апроксимується інтегруючою ланкою де 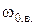- базова частота високочастотної частини ЛАЧХ, яка визначається як частота перетину її першої асимптоти з віссю нуля децибел (горизонтальною віссю) (рис. 3.17).

Нехай, наприклад, низькочастотна частина ЛАЧХ на частоті w = l = 2/Т₀ має нахил –60 дБ/дек (тобто n=3). Тоді і, коли імпульсний елемент є екстраполятором нульового порядку, дискретна передаточна функція має вигляд:

(3.81)

За даними таблиці 3.1 отримуємо:

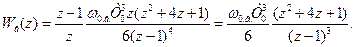
Виконуємо w-перетворення:

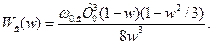
Переходимо до частотної функції:

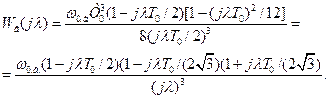(3.82)

Високочастотну частину ЛАЧХ, побудовану за виразом (3.82), наведено на рис. 3.17 праворуч від лінії l=2/Т₀: на частоті l=2/Т₀ нахил ЛАЧХ змінюється на +20дб/дек, а на частоті 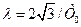- на +40 дБ/дек, оскільки передавальна функція W_в(jl) у чисельнику містить дві ланки з однаковою сталою часу .

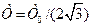Збіг ЛАЧХ для дискретної передаточної функції безперервної частини системи в зоні низьких частот дає можливість виконувати синтез корегуючих пристроїв (цифрових регуляторів) відомими методами синтезу корегуючих пристроїв неперервних систем і використовувати розроблені для них номограми, графіки і таблиці.

Внаслідок синтезу методом ЛАЧХ знаходять ЛАЧХ корегуючого пристрою L_к(l) і за її виглядом визначають комплексну частотну функцію W_к(jl). Після цього виконують підстановку:

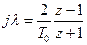, (3.83)

визначають дискретну передаточну функцію W_к(z), а потім різницеве рівняння корекції, яке реалізується цифровим регулятором.

Запитання для самоперевірки

1. Дайте визначення цифрової системи автоматичного керування.

2. Що таке АЦП? ЦАП?

3. Наведіть спрощену функціональну схему ЦС.

4. Які методи застосовують для дослідження цифрових систем?

5. Сформулюйте критерій абсолютної стійкості ЦС.

6. Чому періодичні режими у ЦС не можна називати автоколиваннями?

7. У чому полягає особливість побудови логарифмічних характеристик цифрових систем у низькочастотній і високочастотній зонах?

8. Наведіть передавальні функції цифрових фільтрів.

9. Поясніть методику синтезу коректувального пристрою в цифрових системах за допомогою ЛАЧХ.

4. Одноконтурні та багатоконтурні системи

Одноконтурна система (рис.4.1) є найбільш простим та самим розповсюдженим типом систем, які забезпечують управління вихідною величиною об’єкта управління, тобто вирішення простих задач стабілізації та слідкування. До складу пристрою управління одноконтурної системи автоматичного управління входить задаючий блок ЗБ та регулятор вихідної величини Р. ЗВ – блок зовнішніх впливів. Задача системи полягає в мінімізації відхилення 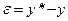, чому перешкоджає збурення та ненульове початкове розузгодження . Задача вирішується за допомогою регулятора виходу.

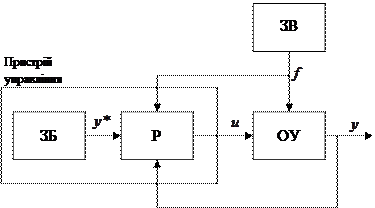Рис.4.1. Одноконтурна система

Замкнута система називається одноконтурною, якщо при її розмиканні в будь-якій точці замкнутого контуру отримаємо коло без паралельних та зворотніх з’єднань.

Замкнута система називається багатоконтурною, якщо при її розмиканні в будь-якій точці замкнутого контуру отримаємо коло, в якому наявні паралельні або зворотні з’єднання.

Багатоконтурна система не має перехресних зв’язків, якщо будь-які два контури, утворені паралельними або зворотніми з’єднаннями, не мають спільних ділянок, або якщо якісь два контури мають спільну ділянку, то один з них знаходиться всередині другого.

Багатоконтурна система має перехресні зв’язки, якщо вона містить два контури, які мають спільну ділянку, і при цьому жоден з них не розміщується всередині другого.

Одноконтурні системи регулювання використовують зазвичай для регулювання одного параметру технологічного процесу а також для стабілізації певного параметру.

Більшість об’єктів хімічної технології характеризуються значними збуреннями та наявністю запізнення. Використання одноконтурних систем при автоматизації таких об’єктів не дозволяє забезпечити високих показників якості регулювання, тому для підвищення якості регулювання таких об’єктів використовують більш складні системи регулювання. Зокрема до таких систем відносяться й багатоконтурні системи автоматичного регування. До багатоконтурних систем відносяться каскадні системи, системи комбінованого регулювання, каскадно-комбіновані системи, системи співвідношення потоків та ін.

Комбіноване управління

Під комбінованим управлінням розуміють такий метод побудови замкнутих систем автоматичного управління, коли разом з управлінням за відхиленням чи за похибкою, використовують управління за задаючою чи збурюючою дією. Таким чином в системі комбінованого управління здійснюється вплив на об’єкт по двох каналах: розімкнутому та замкнутому. За допомогою розімкнутого каналу забезпечується швидкий вплив на об’єкт ще до відхилення регульованої величини, а за допомогою замкнутого контуру зворотнього зв’язку здійснюється якісне підтримання регульованої величини на заданому рівні шляхом поточного контролю похибки регулювання. Структурна схема комбінованої системи управління представлена на рис. 4.2

Рис. 4.2. Структурна схема комбінованої системи управління:

ОР- об’єкт регулювання; ИП, ИПв - вимірювальні перетворювачі; АР – автоматичний регулятор; АРв – автоматичний регулятор за збуренням: ИУ – виконавчий механізм

Впровадження коректуючого імпульсу за найсильнішим збуренням уможливлює істотне зниження динамічної помилки регулювання за умови правильного вибору та розрахунку динамічного пристрою, який формує закон зміни цього впливу.

Основою розрахунку подібних систем є принцип інваріантності.

Принцип інваріантності

Реалізація принципу інваріантності є ефективним засобом усунення протиріч між умовами точності в усталених та перехідних режимах шляхом компенсації зовнішніх збурень.

Термін інваріантність означає незалежність однієї фізичної величини від іншої. В системах управління розглядають незалежність вихідних величин від (керованої величини чи сигнала помилки) від вхідних впливів. В системах стабілізації прагнуть отримати незалежність керованої величини від збурюючих впливів, а в слідкуючих – незалежність сигнала помилки від задаючого впливу. В багатомірних системах з декількома контурами управління прагнуть незалежності кожної керованої величини від "чужих" керуючих впливів, які в контурі управління обраною величиною є збуреннями.

Система є інваріантною по відношенню до збурюючої дії, якщо після завершення перехідного процесу, який визначається початковими умовами, керована величина і похибка системи не залежать від цього впливу. Система є інваріантною відносно до задаючого впливу, якщо після завершення перехідного процесу, що визначається початковими умовами, похибка системи не залежить від цього впливу.

Багатомірні системи управління

До багатомірних відносяться системи управління, які мають кілька керованих величин . Це зустрічається в багатьох сучасних складних системах. До них відносяться, наприклад, системи стабілізації напруги та частоти синхронних генераторів, системи управління рухомих об’єктів, багато систем управління технологічними процесами та ін.

Багатомірна система передбачає наявність багатомірного об’єкта управління (рис. 4.3), який характеризується наявністю кількох входів (точок прикладання управляючих та збурюючих дій) та кількох виходів, які визначаються керованими величинами.

Рис. 4.3. Схема багатомірного об’єкта управління

Багатомірний об’єкт описується системою рівнянь, якку зручно представляти в матричній формі.

Введемо 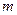-мірну матрицю-стовпець керованих величин

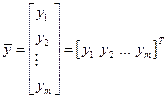, (4.1)

-мірну матрицю-стовпець керуючих впливів

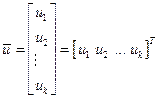, (4.2)

та -мірну матрицю-стовпець збурюючих впливів

. (4.3)

Тут індексом "Т" позначено операцію транспонування матриці.

Якщо керовані величини мають однакову фізичну розмірність і можуть трактуватися як проекції певного вектора на осі координат, то матриця-стовпець може бути тотожною цьому вектору. Тоді можна говорити про вектор керованих величин.

Якщо керовані величини мають різну фізичну розмірність, то перехід від матриці-стовпця до вектора можливий, якщо ввести в матрицю-стовпець вагові коефіцієнти, які б урівнювали розмірності окремих складових. Однак такий перехід не є єдиним і має безліч варіантів.

Аналогічно при рівності фізичних розмірностей окремих складових матриць-стовпців керуючих впливів та збурень можна ввести вектор управління та вектор збурень. При різних фізичних розмірностях окремих складових матриць-стовпців перехід до вектора можливий, але не буде єдиним.

Лінеаризовані рівняння руху багатомірного об’єкта можуть бути записані у матричному вигляді:

. (4.4)

Тут введено квадратну матрицю операторних коефіцієнтів розміром

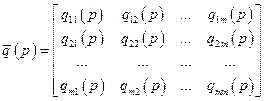(4.5)

та прямокутні матриці операторних коефіцієнтів розміром 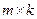та

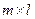
; (4.6)

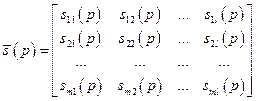. (4.7)

Якщо у виразах (4.1) – (4.7) перейти до зображень Лапласа при нульових початкових умовах, то матричне рівняння (4.4) можна записати для зображень в наступному вигляді:

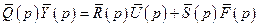. (4.8)

Тут 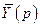, та - матриці-стовпці зображень керованих величин, керуючих впливів та збурень.

В рівняння (4.8) входять також квадратна матриця 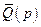та прямокутні матриці 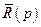та 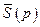розмірами , 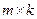та 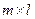відповідно.

Якщо матриця 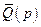не особлива, тобто її визначник не рівний нулю, то, домноживши ліву і праву частини (4.8) зліва на обернену матрицю отримаємо

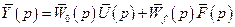. (4.9)

Тут введено матриці передаточних функцій об’єкта для керуючих впливів

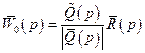(4.10)

та для збурень

. (4.11)

В (4.11) символом 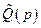позначено матрицю, приєднану для матриці 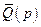. Формули (4.9) – (4.11) дозволяють отримати зв’язок між керованими величинами та керючими і збурюючими впливами.

На рис. 4.4. зображено умовну структурну схему замкнутої багатомірної системи.

Рис. 4.4. Структурна схема замкнутої багатомірної системи

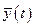На схемі всі вказані символи відповідають матрицям: - задаючих впливів, - керованих величин, - похибок для кожної керованої величини, 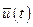- керуючих впливів, - збурень, 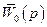- передаточних функцій для управління, - передаточних функцій для збурень. Крім того введено прямокутну матрицю передаточних функцій керуючого пристрою , яка визначає алгоритми управління. Вона дає зв’язок між зображеннями керуючих впливів та похибок:

. (4.12)

Рівняння багатомірної системи (рис. 4.4) можна отримати наступним чином.

Матриця передаточних функцій розімкнутої за всіма каналами системи

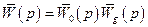. (4.13)

Характеристична матриця системи являє собою квадратну матрицю розміром :

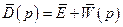. (4.14)

Тут - одинична матриця розміром , тобто квадратна матриця, у якої всі елементи головної діагоналі рівні одиниці, а решта – нулю.

Характеристичне рівняння системи отримуємо, прирівнявши до нуля визначник характеристичної матриці:

. (4.15)

Зазначимо, що у випадку, коли багатомірна система є сукупністю 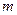незалежних одномірних систем, характеристична матриця буде діагональною і визначник системи тоді рівний добутку окремих визначників кожної з систем, тобто 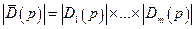. В цьому випадку загальне характеристичне рівняння розпадається на 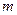незалежних характеристичних рівнянь , .

Матриці передаточних функцій замкнутої системи, за помилкою та за збуреннями, за умови, що матриця 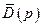не особлива, що означає незалежність вихідних диференціальних рівнянь, можуть бути визначені з виразів

, (4.16)

, (4.17)

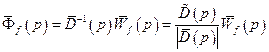. (4.18)

Тут 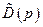- матриця, приєднана для матриці .

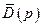7 ОПТИМАЛЬНІ СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ

Одним з видів автоматичного керування є оптимальне керування, яке застосовують у технічних системах для підвищення ефективності виробничих процесів, і в системах організаційного управління для вдосконалення діяльності підприємств та організацій. Ідея оптимізації в останні десятиріччя була центральною ідеєю, яка визначала розвиток теорії керування.

Слово “оптимальний” походить від латинського optimus, що значить – найкращий, досконалий. Оптимізація – це отримання найкращого можливого рішення.

Сучасна постановка задач оптимального керування (з точністю до термінології) була виконана у роботі російського вченого Д.Є. Охоцимського “К теории движения ракет” (1946 р.). Теорію оптимальної швидкодії вперше було викладено в роботах О.А. Фельдбаума, який у 1953-1956 роках запровадив поняття оптимальних за швидкодією процесів. Видатна роль у розвитку теорії оптимального керування належить академіку Л.С. Понтрягіну, який 1956 року сформулював принцип максимуму, що являє собою єдиний математичний апарат теорії оптимальних за швидкодією процесів для систем з декількома керуючими органами у разі обмежених за модулем координат керування. Після робіт Понтрягіна та його школи в теорії оптимального керування відбулася та канонізація методів і мови, яка свідчить про появу нової дисципліни “Теорія оптимального керування”.

Дата добавления: 2014-01-07