Обмеження фазових координат і керувань

Постановка й класифікація задач оптимізації

Під час розробки автоматичних систем насамперед ставиться задача виконання функціонального призначення системи, що визначається метою керування. Більш складною є задача розробки системи з найкращими показниками якості – оптимальної системи. Оцінку досяжності мети у процесі керування об’єктом, яка подана у формалізованому вигляді, називають критерієм оптимальності або цільовою функцією. Розробка оптимальної системи - це задача синтезу або задача оптимізації.

Розв’язання цієї задачі починають з її постановки, яка містить опис заданих реальних елементів системи математичними співвідношеннями (складення математичної моделі системи), визначення існуючих обмежень для координат системи й аналіз характеристики сигналів зовнішніх впливів, а також складення математичного виразу заданого критерію якості. Далі задачу розв’язують відповідними математичними методами, у результаті чого знаходять функцію керування за умови мінімуму чи максимуму показника якості, що визначає оптимальний режим роботи об’єкта.

Об’єкт керування можна подати у вигляді, що наведений на рис. 10.1. Величини u₁(t), …, u_m(t) зручно вважати координатами деякого вектора u = (u₁, u₂, …u_m) у m-мірному просторі керування. Вектор u називають вектором керування або керуванням.

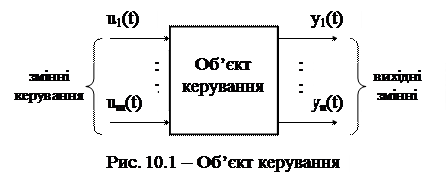Величини y₁(t), …, y_n(t) розглядають як координати вектора y = (y₁, …, y_n) у n-мірному просторі, який називають фазовим простором об’єкта, що розглядають. Вектор y називають фазовим вектором або вектором стану. Він визначає стан об’єкта у даний момент часу. Якщо стан об’єкта характеризується двома фазовими координатами, то кажуть про фазову площину. Розмірність векторів u і y може бути однаковою або відрізнятися одна від одної (m£n). Пару векторних функцій [ u (t), y (t)] називають процесом керування або просто процесом.

Під час розробки оптимальних систем автоматичного керування необхідно враховувати різні обмеження, що накладають на координати і показники якості процесу.

Усі обмеження координат і керувань можна розділити на два типи: природні та умовні.

Природні обмеження фазових координат обумовлені принципом роботи об’єкта. Наприклад, частота обертання асинхронного електродвигуна не може бути більшою за синхронну частоту; вихідні сигнали підсилювача обмежені через явище насичення і т.д.

Умовні обмеження координат уводять свідомо. Наприклад, величину струму якоря електродвигуна постійного струму обмежують умовами нормальної комутації на колекторі, нагрівом струмопровідних частин, граничною температурою ізоляції обмоток. Наявність умовних обмежень координат звичайно обумовлює введення обмежень на керування.

Іншими словами, вектори u (t) і y (t) можуть змінюватись лише у деякій зоні, що допускається:

u (t) 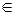G_u; y (t) 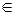G_y. (10.1)

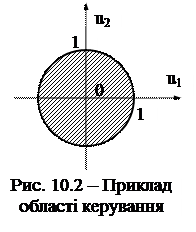Першу умову називають обмеженням на керування, другу – фазовим обмеженням. G_u і G_y – деякі задані множини. Множину G_u називають областю керування. Її вказують у математичному описі об’єкта. Наприклад, якщо параметри u₁ і u₂ характеризують на площині векторну величину, модуль якої не перевищує одиниці, а напрямок довільний, то ці параметри підкоряються умові 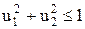, а область керування G_u являє собою круг одиничного радіусу (рис. 10.2).

У загальному випадку область керування може мати геометрично більш складний характер, оскільки через конструкцію об’єкта між керуючими параметрами u_i можуть існувати зв’язки, що виражаються рівняннями вигляду:

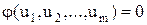. (10.2)

Для технічних систем особливо важливим і характерним є випадок замкнутої множини G_u, тобто випадок, коли точка може знаходитись не тільки всередині цієї множини, а і на її межі.

Важливо зробити ще одне припущення: значення керуючих параметрів можуть змінюватися стрибком, тобто ці параметри є безінерційними. Тому необхідно розглядати не тільки безперервні, а й кусково-безперервні керування.

Функція u(t) при t₀ £ t £ t₁ називається кусково-безперервною, якщо складається зі скінченної кількості безперервних кусків, тобто є безперервною для всіх моментів часу t, за винятком лише скінченної кількості цих моментів, де функція u(t) може мати розрив першого роду (рис. 10.3).

Кусково-безперервні керування дозволяють отримати для достатньо широкого класу прикладів точний математичний розв’язок оптимальної задачі та є достатньо наочними і зручними для технічної реалізації.

Дата добавления: 2014-01-07