Метод найшвидшого спуску

За цим методом напрямок градієнта визначається у початковій точці, а потім здійснюється рух у цьому напрямку доти, доки похідна вздовж цього напрямку dI/dt не дорівнюватиме нулю. Потім знову визначається напрямок градієнта і здійснюється рух за новим напрямком до наступного нульового значення похідної і т.д.

Метод найшвидшого спуску характеризується відносно малим часом досягнення екстремуму при великих кроках на початковому етапі пошуків.

Приклад 11.1 Задано показник екстремуму:

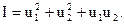(11.6)

Визначити мінімум функції I(u₁, u₂) методом найшвидшого спуску з початкової точки u₁₀ = 4; u₂₀ = 6.

Функції I(u₁, u₂) відповідає сім’я еліпсів для різних I = const (рис. 11.10). Початковий стан визначається точкою М₁.

Знайдемо напрямок градієнта у початковій точці. Частинні похідні для цієї точки:

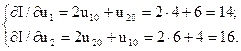(11.7)

Через те, що відшукуємо мінімум функції І, будемо рухатись у напрямку, зворотному до градієнта, і визначимо координати u₁₁, u₂₁ наступної точки:

(11.8)

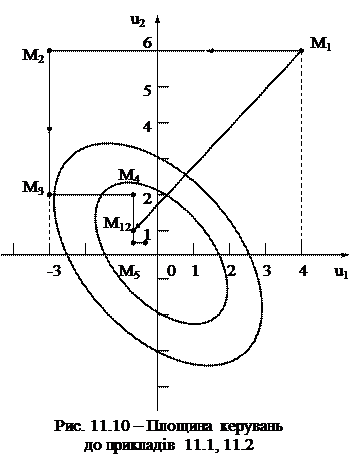де L – поки ще невідомий крок переходу з точки (u₁₀, u₂₀) до точки (u₁₁, u₂₁).

Для визначення кроку L підставимо знайдені значення u₁₁, u₂₁ у вираз (11.6):

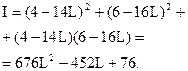
Прирівняємо до нуля похідну і отримаємо:

звідки L = 0,334.

Підставимо це значення у вираз (11.8) і визначимо координати u₁₁ і u₂₁:

u₁₁ = -0,68; u₂₁ = 0,65 (точка М₁₂ на рис. 11.10).

Виконавши аналогічні обчислення для наступного кроку за умови, що вихідним станом системи є стан, у який вона прийшла у кінці першого кроку, дістанемо: u₁₂ = 0,0229; u₂₂ = 0,0362. Отже, практично за два кроки система опиняється у точці, досить близькій до точки мінімуму.

Метод Гаусса-Зейделя (метод почергового змінювання параметрів)

За цим методом рух уздовж кожної координати відбувається по черзі. Спочатку здійснюється рух уздовж координати u₁, а решта координат u₂, u₃, … залишаються незмінними. Цей рух триває доти, доки похідна функції І по координаті u₁ не дорівнюватиме нулю, тобто 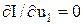. З останньої умови визначається u₁. Після цього значення u₁ і решта координат, крім u₂, залишаються незмінними, а координата u₂ змінюється доти, доки не буде виконана умова . З цієї умови визначається u₂. Потім змінюється координата u₃ і т.д. У такій спосіб визначаються частинні екстремуми по всіх координатах. Після цього виконується повторний цикл змінювання координат по черзі, починаючи з u₁. Процес пошуку триває, доки всі частинні похідні не дорівнюватимуть нулю (доки всі похідні не будуть меншими за поріг чутливості системи).

Приклад 11.2 Розв’язати задачу (приклад 11.1) методом Гаусса-Зейделя.

Початковий стан об’єкта визначається точкою М₁ (рис. 11.10). Починаємо пошук, змінюючи координату u₁ при u₂ = 6. Тоді

Визначимо частинну похідну даної функції за u₁ і прирівняємо її до нуля:

звідки для першого частинного екстремуму u₁ = -3. Йому відповідає точка М₂ з координатами u₁ = -3, u₂ = 6.

Фіксуємо параметр u₁ = -3 і змінюємо координату u₂:

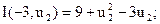
u₂ = 1,5.

Цьому значенню координати u₂ відповідає точка М₃.

Повторимо обчислення для координати u₁ при u₂ = 1,5:

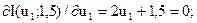u₁ = -0,75.

Отримали точку М₄(-0,75;1,5).

Наступний цикл:

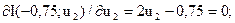u₂ = 0,375.

Цьому циклу відповідає точка М₅.

Отже, пошукові рухи становлять ламану лінію, яка складається з взаємно перпендикулярних відрізків. Точки зламу є точками дотику цих відрізків до кривих I(u₁,u₂)=const.

Метод змінювання параметрів зручний тим, що для його реалізації можна застосовувати відомі типи однопараметричних екстремальних систем, якщо додати пристрій, що перемикає канали параметрів u₁, u₂, …, u_m. Проте, як видно з рис. 11.10, рух системи до екстремуму відбувається далеко не найкоротшим шляхом.

Дата добавления: 2014-01-07