Динаміка екстремальних систем

Метод статистичного найшвидшого спуску

Метод статистичного градієнта

Метод випадкових сліпих пошуків

Суть методу полягає у пошуку екстремуму за рахунок випадкового змінювання параметрів u_i. У початковому стані системи координатам u_i дається випадковий приріст і визначається приріст функції І. Якщо він від’ємний (при пошуках максимуму), то система повертається у початковий стан і робиться наступний пробний крок. Так повторюється доти, доки не дістанемо додатний приріст. Тоді система переводиться у цей новий стан, з якого робляться нові випадкові кроки.

Цей метод полягає у тому, що з початкового стану системи робиться кілька пробних випадкових кроків і для кожного з них знаходиться приріст функції І. За цими приростами, як за складовими вектора, визначається напрямок найбільш інтенсивного змінювання функції І. У цьому напрямку виконується робочий крок, а потім цикл пошуків повторюється.

Початок пошуків такий самий, як у попередньому методі, але після визначення напрямку робиться не один крок, а рух відбувається, доки не зміниться знак приросту І.

Під час випадкових пошуків немає потреби визначати залежності І від кожної координати u_i окремо. Це особливо важливо при великій кількості координат, тому що при збільшенні їх кількості, на відміну від розглянутих детермінованих методів пошуку, процедура пошуків не ускладнюється. Доведено, що при і>3 випадкові пошуки перевершують детерміновані за швидкістю досягнення екстремуму.

Іншою перевагою методу випадкових пошуків є можливість відшукати глобальний екстремум при наявності кількох екстремумів, а також при наявності особливих точок, для яких grad I = 0. Детерміновані методи, що базуються на пошуках точки з нульовим градієнтом, у цих випадках непридатні, тому що система може припинити пошуки на будь-якому локальному екстремумі або в особливій точці.

У деяких випадках найефективніше об’єднувати різні методи пошуків. Зокрема, на початку пошуків далеко від точки екстремуму можна застосувати метод найшвидшого спуску, а поблизу екстремуму перейти до градієнтного методу.

Екстремальні системи повинні задовольняти таким вимогам:

- стійкості, під якою розуміють збіжність процесу пошуку в деякому околу екстремуму;

- точності – забезпечення заданого відхилення критерію ефективності від екстремального значення в усталеному режимі;

- швидкодії – забезпечення можливо меншого часу пошуку екстремуму.

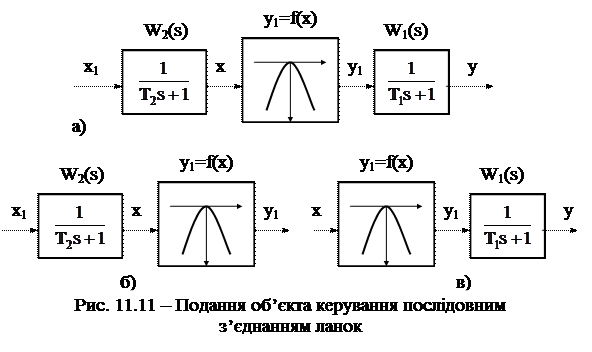
Під час дослідження динаміки СЕК керований об’єкт можна апроксимувати послідовним з’єднанням трьох ланок з коефіцієнтом підсилення, що дорівнює одиниці. Візьмемо, що кожну інерційну ланку описують лінійним диференціальним рівнянням першого порядку (рис. 11.11,а).

У цьому випадку об’єкт описують системою рівнянь:

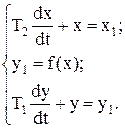(11.9)

де х₁ – вхідна координата об’єкта, y – вихідна координата об’єкта.

Інерційна ланка зі сталою часу Т₂ (на вході об’єкта) звичайно з’являється у структурній схемі об’єкта керування тоді, коли виконавчий механізм діє на об’єкт оптимізації через інерційну ланку, наприклад, якщо входом х об’єкта, що оптимізується, є температура, а виконавчий механізм діє на неї через теплообмінник.

Якщо стала часу виходу об’єкта значно менше за сталу часу на його вході, тобто Т₁<<Т₂, то інерцією виходу об’єкта можна знехтувати, а об’єкт апроксимувати послідовним з’єднанням двох ланок (рис. 11.11, б).

Якщо Т₂<<Т₁, то можна знехтувати інерцією входу, і тоді структурна схема матиме вигляд, наведений на рис. 11.11, в. Диференціальне рівняння такого об’єкта можна записати у вигляді:

(11.10)

Дата добавления: 2014-01-07