Сигналы с ограниченным спектром

При построении метода дискретизации аналогового сигнала необходимо сформулировать критерий выбора дискретных отсчетов, установить процедуру восстановления по ним исходного сигнала и иметь возможность определять возникающую при этом ошибку. Решение указанной задачи возможно лишь на базе выбора определенной математической модели дискретизируемого сигнала. Наибольшее распространение получила модель сигнала с ограниченным спектром. В этом случае величина шага дискретизации ставится в соответствие с наивысшей частотой, присутствующей в спектре сигнала.

Сигналом с ограниченным спектром называют сигнал, математическая модель которого обладает следующим свойством – спектр сигнала принимает ненулевые значения лишь в ограниченной полосе частот от нуля до граничной частоты 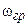. С физической точки зрения такая модель сигнала оправдана тем, что вклад спектральных составляющих при 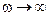пренебрежимо мал в силу ограниченности энергии сигналов. Необходимо учесть и то, что любое реальное устройство, предназначенное для передачи и обработки сигналов, имеет конечную ширину полосы пропускания.

Примером сигнала с ограниченным спектром может служить идеальный низкочастотный сигнал (рисунок 3), спектральная плотность которого описывается функцией:

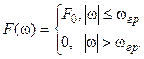
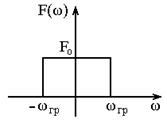
Рисунок 3 – Спектр идеального низкочастотного сигнала

Математическую модель идеального низкочастотного сигнала (ИНС) во временной области можно получить из формулы обратного преобразования Фурье:

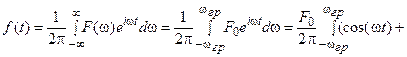
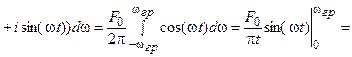
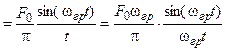. (1)

Для построения графика функции (1) рассмотрим несколько частных случаев:

1) ;

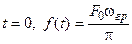2) ;

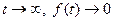3) 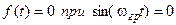, откуда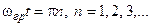

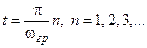
График ИНС (рисунок 4) имеет вид осциллирующей кривой, четной относительно начала отсчета времени. С увеличением граничной частоты спектра возрастают как центральный максимум, так и частота осцилляций.

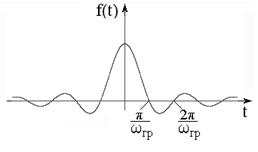
Рисунок 4 – Идеальный низкочастотный сигнал

Дата добавления: 2014-01-07