Производственные функции

Производство товаров можно подразделить на несколько направлений:

1. Производство товаров материальных.

2. Энергетических.

3. Услуги (перевозки, химчистки)

Эти товары проходят и стадии:

1. Производство.

2. Потребление.

3. Обмен.

4. Распределение.

Каждое из этих производств может быть описано в одной из измерительных систем и представлено аналитически. Модельно зависящей от факторов, порождающих тот или иной вид операций с товарами. При моделировании в первую очередь на 1-ом этапе формулируют все наименования товара, выбор единицы измерения. Далее производится производство, потребление и т.д. Производственная декомпозиция на подсистемы с описанием потоков этих товаров. После определения факторов, влияющие на товары для формирования модели, формируется балансное отношение. Поскольку потребление этих благ не может превышать их производство. И далее формируются ограничения на суммарном производстве товаров. Поскольку производство не может быть ограничено. Эти 3 компонента: модель, баланс и ограничения составляют основу анализа производства. Под производственной функцией будем называть соотношение между используемыми в производстве фактами и выпускаемой продукцией. Измерение фактов приводит либо к одним единицам, либо к относительным величинам. Вектор производственных факторов определяется ресурсами производства.

Соответствие продукции производства

Производственная функция может быть определена следующим образом:

,

где 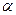- вектор параметров некоторой аналитической зависимости между Y и X.

Различают производственные функции в следующих формах:

1. В форме функции выпуска продукции.y=f (x, ).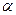

2. x=h(y,ά) как функция производственных затрат.

Вторая форма используется в том случае, когда не допустимо замещение одного ресурса другим. Обе функции подразумевают, что имеется некоторое множество производственных возможностей:

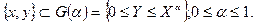
При анализе производственной функции, анализируют граничные значения, поскольку именно там достигаются оптимальные величины.

Производственные функции имеют следующие свойства:

1. Производство невозможно при отсутствии хотя бы одного ресурса.

Это свойство обозначает, что отсутствие одного из ресурсов не может быть заменено другим ресурсом.

2. При увеличении производственных затрат выход продукции не уменьшается.

Если производственная функция дифференцируема, то можно выразить следующие зависимости:

,

где 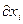- предельная эффективность. Она характеризует отношение прироста выпускной продукции к малому приросту i-го ресурса. При постоянных значениях остальных ресурсов. Эффективность характеризует производственную функцию в одной точке. Поэтому часто используют интегральную или среднюю эффективность i-го ресурса, который определяется как

Для производственной функции нашего примера представленная эффективность будет определяться:

Кроме предельной и средней эффективности, в качестве характеристики изменения выпуска продукции при изменении затрат используют отношения этих величин, которая называется эластичностью выпуска продукции по отношению к изменению количества i-го ресурса. Эта величина тоже является предельной. Формально ее можно определить как предел отношения приращения выходного продукта к приращению продукта.

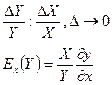
В общем виде: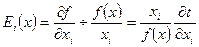

Величину эластичности для каждого ресурса можно определить по-другому:

Эластичность выпуска, по какому либо ресурсу, показывает, насколько изменится % выпуска продукции, если объект соответствующего ресурса изменился на 1%.

3. По мере увеличения одного ресурса и постоянном количестве других,

предельная эффективность этого ресурса не возрастает. Математически это свойство производственной функции будет означать, что производство по этому ресурсу будет

не >0.

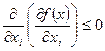
Это свойство обозначает, что рост факторов производства, т.е. рост ресурсов приводит к росту выпуска продукции, но темп производства падает. Содержательная интерпретация заключается в том, что с увеличением одного из фактора при постоянных других, соотношение между ними увеличивается, и каждая единица других этого фактора работает с меньшим количеством единиц других факторов. Таким образом, получается, что эффективность использования этого фактора уменьшается.

4. При пропорциональном изменении всех видов ресурсов, изменения выпуска

продукции характеризуется возрастающей постоянной или убывающей отдачей от расширения масштабов производства. Математически производство этой функции предполагает однородность производственной функции.

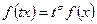
Если σ > 1 будет возрастать производство.

σ =1 и σ < 1 –убывающее.

Для нашей функции:

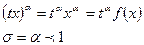
Например, для функции:

При возрастании производственной функции отдача производства будет увеличиваться. Для характеристики изменения масштаба производства, используют предельную величину Е (х), которую называют эластичностью производства.

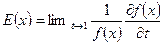
Между эластичностью производства и эластичностями выпуска по каждому ресурсу имеются соотношения.

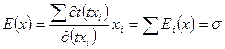
Таким образом, эластичность всего производства, определяется суммой эластичностей выпуска продукции, по отношению к каждому ресурсу.

Предельные величины для описания возможности замещения ресурсов.

Для аналитического описания возможности замещения одного ресурса на другой, при получении такого же количества продукции, вводится понятие изокванты.

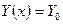
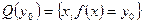
Изокванты обладают следующими свойствами:

1. Они не пересекаются между собой.

2. Изокванта развивает не отрицательный ортант на 2 области:

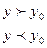
3. Большему выпуску продукции, соответствует изокванта более удаленная от

начала координат. Изокванта может быть представлена, как зависимость 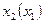и эту зависимость можно не явно определить. В явном виде она будет выглядеть:

Зависимость 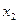от не всегда однозначно определяется исходной производной функцией. Зависимость (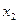) монотонно убывающая функция.

Если по каждой переменной дадим незначительные приращения, а в силу малости этого приращения функция будет равна значению функции в исходной точке. Из равенства можно вывести следующее уравнение:

Величина называется предельной нормой замещения одного ресурса другим. Для функции 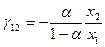с уменьшением одного ресурса на предельную норму, другой ресурс должен увеличиваться на эквивалентную предельную норму. Предельная норма может быть в функции либо от ресурсов, либо от величины замещения по ресурсам. Если для элементов факторной модели, то эта величина будет const 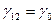,то 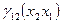называют изоклинами.

Для количественной характеристики скорости изменения предельной нормы вдоль изокванты, вводится предельная величина, которая называется- эластичность замещения ресурсов.

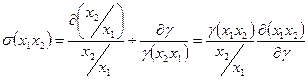
Содержательный смысл этой величины сводится к тому, что ее значение показывают, на сколько процентов должно уменьшится отношение ресурсов и сохранении постоянного выпуска продукции, чтобы при этом предельная норма замещения одного ресурса другим изменилась на 1%.

Эластичность замещения также можно определить по следующей формуле:

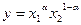
Дата добавления: 2014-01-07