Структурные схемы измерения

1. прямого преобразования

2. компенсационного преобразования

2.1 с астатической характеристикой

2.2 со статической характеристикой

3. с автоматической коррекцией погрешности

1.Структурные схемы измерения прямого преобразования

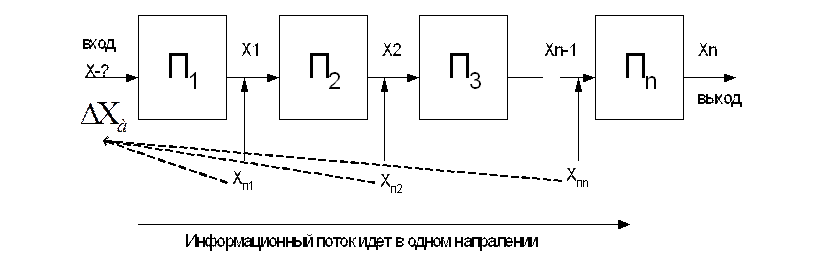Найти: Хп=F(x) – функция всего устройства в целом.

Функции преобразования отдельных блоков могут быть линейными и нелинейными. Пусть все функции линейные:

…

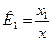
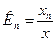
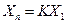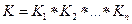Функции преобразования: , где (1)

Возникают погрешности:

1. 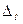←←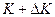←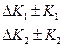влияние внешних факторах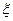

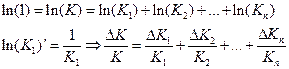
Идеальный случай: Хп=КХ при всех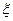

Реальный случай: 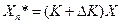при всех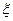

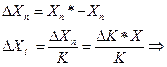
При последовательном включении блоков их число ограничено.

Можно подобрать блоки с различным

2. 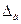←внешние помехи и внутренние дрейфы←Хп

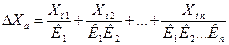
ПРИМЕР:

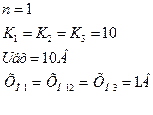
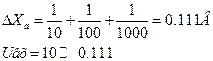
При наличие помехи, первый каскад нужно делать очень тщательно (экранирование, заземление, использование качественных кабелей). Фильтры не всегда помогают, так как они влияют на динамику.

2. Структурные схемы измерения компенсационного преобразования

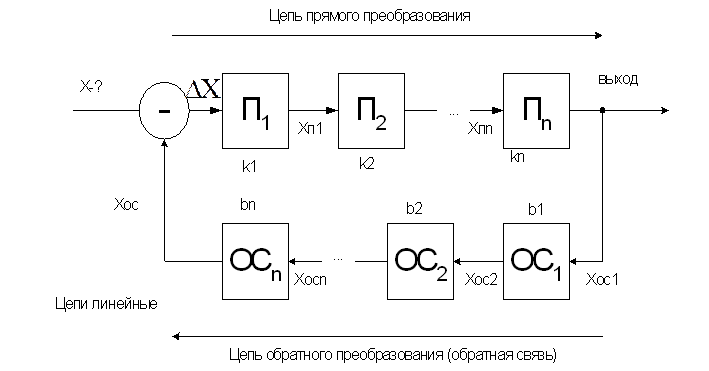
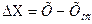
2.1 Структурные схемы измерения компенсационного преобразования с астатической характеристикой

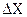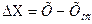=0

=0

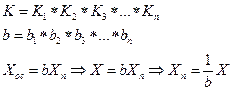- функция преобразования всего устройства

S=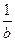- коэффициент преобразования всего устройства

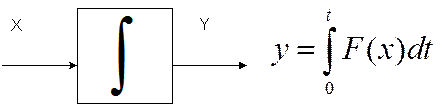Чтобы реализовать такой режим работы, в любом месте цепи прямого преобразования должно стоять запоминающее интегрирующее звено.

В связи с тем, что современные интегрирующие устройства обладают невысокой чувствительностью, то обычно их ставят в конце цепи.

Возникают погрешности:

1.

Цепь отрицательной обратной связи выполняется на пассивных элементахее можно сделать более стабильнойвведение отрицательной обратной связи всегда уменьшает .

2.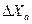←внешние помехи

внутренние дрейфы

порог чувствительности интегратора

Будем считать, что помехи воздействуют на цепь прямого преобразования, так как цепь обратной связи низкоомная. Приведем помехи на вход:

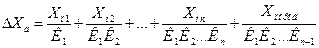
Введение отрицательной обратной связи 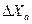не уменьшает.

2.2 Структурные схемы измерения компенсационного преобразования со статической характеристикой

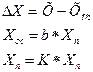
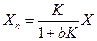- функция преобразования всего устройства

bK-петлевое усиление.

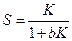- коэффициент S зависит только от b и K.

Возникают погрешности:

1.

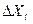
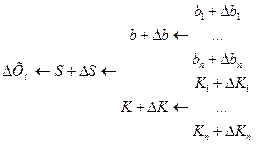
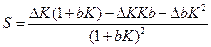
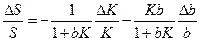
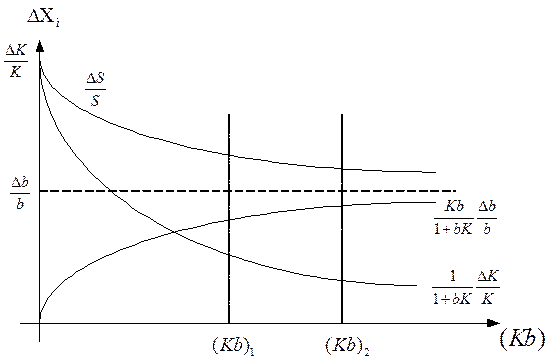
ВЫВОДЫ:

1. при больших Kb, 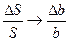, т.е нестабильность всего устройства определяется нестабильностью цепи обратной связивведение отрицательной обратной связи .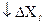

2. При больших Kb, замкнутая система может потерять устойчивость, т.е система будет реагировать не на сигнал, а на внутренние флуктуации

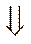
Компромисс между точностью и устойчивостью может быть найден при:

2. вешние помехи, внутренние дрейфы→Хп

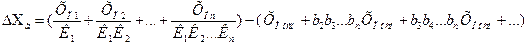
Введение отрицательной обратной связи не уменьшает аддитивную погрешность.

Дата добавления: 2014-01-07