Теория Погрешностей. 1. причины появления погрешностей результата измерений

1. причины появления погрешностей результата измерений

2. погрешности систематические и случайные, описание случайных погрешностей

3. идеи суммирования погрешностей

4. обработка ряда прямых наблюдений для получения результатов измерений

1. причины появления погрешностей результата измерений

схема измерения эксперимента

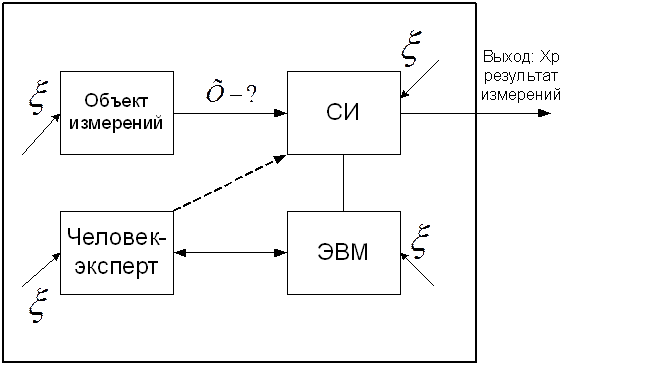
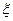-помехи и влияющие факторы

Результат нужен для того, чтобы иметь однозначную информацию об измеряемой величине.

Погрешность результата измерений:

Хр – истинное значение

Хn – результат измерений

Причины:

-погрешность методанесоответствие модели методу

ПРИМЕР:

Объект измерений – генератор

А) модель

V-вольтметр, измеряющий действующее значение

Б) реально:

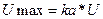
если

если не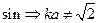

не учитывается, что сигнал отличается от синусоидального

- инструментальная погрешность (ею обладает средство измерения)

- погрешность от влияния средства измерения на объект измерения.

ПРИМЕР:

Есть 3 амперметра:

, т.е если сопротивление амперметра разное, то и ток будет азным, но разность токов эксперимент произведен неверно.

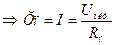- истинное

- погрешность человека-экпериментатора

- погрешность, связанная с ЭВМ (погрешность округления)

2. погрешности систематические и случайные, описание случайных погрешностей

Погрешность результата формируется под воздействием факторов:

I. факторы, которые в процессе измерения остаются постоянными или меняются по закону, следовательно, формируются систематические погрешности

II. факторы, которые в процессе измерения меняются случайным образом с

интенсивностью, которую трудно предсказать, следовательно, формируются

случайные погрешности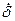

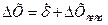, где 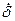- учитывается методами математической статистики

- уменьшается до нуля

ПРИМЕР 1:

можно свести к минимуму

ПРИМЕР 2:

Делая многократные измерения одной и той же величины, можно получить (выявить)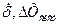

ПРИМЕР 3:

Если устранена, то 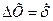, тогда рассчитывается методами теории вероятности.

Как свести к минимуму?

Методы:

1. правильная постановка эксперимента.

2. введение поправочных кривых, графиков и т.д

3. специальные методы

ПРИМЕР:

Случайная величина полностью описывается законами распределения интегрирующими и дифференцирующими (плотностью распределения вероятности). На практике – дифференцирующими законами.

ПРИМЕР:

Известен дифференцирующий закон распределения, следовательно, можно найти вероятность того факта, что измеряемая величина находится между Х1 и Х2.

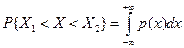
Во многих случаях измеряемая величина распределяется около истинного значения Q (но не всегда).

Плотность распределения погрешностей:

ПРИМЕР:

На практике вместо законов распределения пользуются их оценками числовых параметров (оценки моментов) или числовыми параметрами (моменты)

Как с помощью вероятностных характеристик оценить погрешность?

Оценку погрешности производят с помощью доверительных интервалов и доверительной погрешности:

- доверительный интервал

k- коэффициент, зависящий от р(х) и Рдов

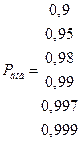применяются такие значения в измерительной технике

3. идеи суммирования погрешностей

1. первый подход

2. второй подход: суммируются погрешности на основании вероятностных характеристик

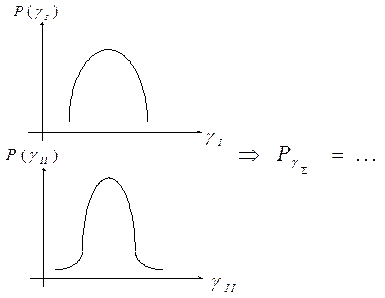
1. если законы распределения не Гауссов, то при n>3 возникают сложности

2. может возникать трансформация закона суммарного распределения.

ПРИМЕР:

при Рдов = …

- суммарное СКО

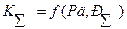
- суммарный закон распределения

На практике существует только 2 значения доверительной вероятности.

ПРИМЕР:

r-коэффициент корреляции (коэффициент связи)

r = 0 – некоррелированы

- коррелированы ()

На практике:

ПРИМЕР:

Примечание:

При суммирование погрешностей обычно аддитивные и мультипликативные составляющие суммируются отдельно друг от друга.

4. обработка ряда прямых наблюдений для получения результатов измерений

Обработка результатов предполагает, что одну и ту же величину измеряют много раз в одинаковых условиях.

Х - измеряемая величина

n>40 – количество измерений - ряд наблюдений

Из ряд наблюдений нужно исключить промахи (по определенным методам).

Ранжирование: Хmin … Xmax

Ищем оценки числовых параметров:

1). оценка математического ожидания

2). оценка СКО:

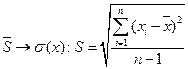
3). найти закон распределения:

гистограмма

1. делится на нечетное число

2. из всех n находим частоту попадания на интервал

3.

3. По виду гистограммы выдвигается гипотеза, какому закону распределения она соответствует.

4. Критерий согласия: например,

Для подсказки в измерительной технике говорится, какие законы распределения наиболее используются:

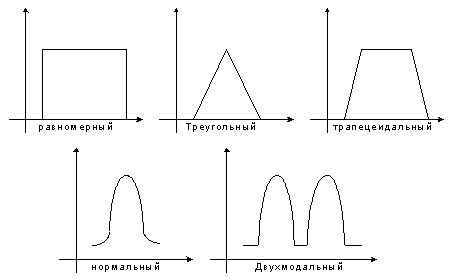
4).

- гарантия разброса относительно среднего с определенной вероятностью

Примечание:

Существуют случаи, когда не нужно строить гистограмму для определенного закона распределения:

- когда имеются статистические данные

- когда закон распределения уже известен

- если результат измерений формируется под действием большого числа независимых факторов, причем вклад каждого фактора в результат одинаков, то можно считать, что закон нормальный (N>5).

- Если закон распределения нормальный, а n>10, то можно пользоваться распределением Стьюдента:

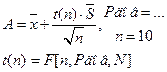
Дата добавления: 2014-01-07