
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Y2\ 122JLt/cJ _ L^2
|
|
|
|
найдём необходимые для (5.1) проводимости. В рассматриваемом случае в схеме нет активных сопротивлений, поэтому Ytj = ytj и а7/- = 0 (см. п.
2.4).
Работу по заполнению матрицы Y уравнений (5.2) и по преобразованию (5.2) к (5.3) необходимо выполнить для каждой из приведённых схем.
Начальными условиями интегрирования при расчётах переходных процессов в электроэнергетических системах являются значения параметров режима и проводимостей схемы после приложения возмущения, но при t = 0. Исходя из составленного описания переходных процессов (5.1), начальными условиями интегрирования будут:
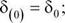
|
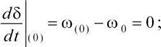
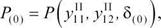
Ю(0) ® 0 ’

|
где 50 - угол ротора в исходном (доаварийном) режиме.
Для интегрирования системы уравнений, описывающей переходные процессы, выберем метод последовательных интервалов. Метод не является особо точным и рекомендуется обычно для ручных вычислений. В (5.1) входит только одно дифференциальное уравнение, поэтому формулы численного интегрирования применяются только для расчёта приращений угла 5 за каждый интервал времени At (шаг интегрирования).
Первый интервал времени. Небаланс мощности на валу ротора генератора в начале интервала времени:
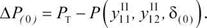
|
Приращение угла за первый интервал времени: Д5т=0,5-С-ДЛ0); С
(V ~ ^ ^ ^(0)-' т
1 j
Значение угла к концу первого интервала времени:
= S(oj +
Приращение и новое значение угла к концу интервала к > 1:
^P(k-i) = Р, ~р{у{\ ’ У\г >
^(к) =)+С ' АР(к- 1) >
^(к) = ^(к-\) + ^ (к)'
Исключение составит интервал времени m первый после отключения повреждённого элемента системы. В этом интервале времени в расчёт должны быть введены проводимости схемы в послеаварийном режиме
У1\\> Уп • Происходит скачкообразный переход с характеристики мощности аварийного режима уЦ, б) на характеристику мощности по-
слеаварийного режима Z5^ v''1, у™, 8 j. Расчёт первого интервала времени
после скачка в методе последовательных интервалов отличается от других интервалов:
^Р(т-\) = Р\ ~Р[У\\> У\2> ^(т- 1;)’
ЬС-и = Рт-р(Уп’Уи.Ь1т-иУ’
= &Ь(т-ч + 0,5-С-(дР(” _v + ДРД'.и);
^(т) ~ ^(т-1) т) ■
Выполняя последовательно интервал за интервалом описанные расчёты, строится зависимость 5(7) (рис. 5.6).
 Рис. 5.6. Изменение угла 5 в переходном режиме
Рис. 5.6. Изменение угла 5 в переходном режиме
|
Заключение об устойчивости. При составлении математического описания переходных процессов (5.1) был принят целый ряд допущений. В результате система уравнений (5.1) описывает поведение не реальной, а некоторой идеализированной системы. При этом оказалось, что правая часть дифференциального уравнения не зависит от производных режимных параметров, а определяется только их величинами (позициями). Системы, поведение которых описывается такими уравнениями, называются позиционными. Для позиционных систем характерно то, что колебания в них, однажды возникнув, не затухают с течением времени. В действительности, при более полном учёте факторов, влияющих на движение ротора генератора, например, переходных процессов в обмотке возбуждения, возникшие колебания затухнут, и в системе наступит установившийся режим.
Таким образом, в рассматриваемом случае колебательные изменения угла 8 будут свидетельствовать об устойчивости электроэнергетической системы. Если же при t —> со и 8 —» оо, то электроэнергетическая система в рассматриваемом режиме при заданном возмущающем и управляющем воздействии неустойчива.
5.3. Энергетические соотношения, характеризующие движение ротора генератора. Способ площадей
Для простейшей электроэнергетической системы (см. рис. 5.1) при описании переходных процессов в ней уравнениями (5.1) характер относительного движения ротора эквивалентного генератора станции после отключения КЗ можно установить, рассматривая энергетические соотношения сил, действующих на ротор.
Определив проводимости схемы уп, у12 для нормального, аварийного и послеаварийного режимов, можно построить характеристики мощности эквивалентного генератора станции для этих режимов:
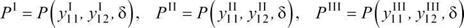
|
| (рис 5.7). |
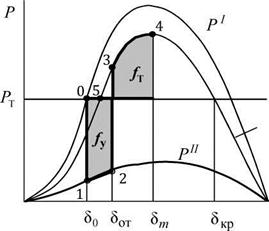
Нормальный режим будет соответствовать точке 0, в которой уравновешены электромагнитная мощность генератора и мощность турбины. В первый момент КЗ угол 8 (инерционная координата) скачком измениться не может, 8^ = 80, и поэтому новый режим будет отвечать точке 1 на
характеристике мощности Ри режима КЗ. Так как теперь генератор будет
отдавать меньшую мощность, чем он получает от турбины, то под действием избыточного момента ДМ* = AR, = PT,f - R, ротор генератора начнёт ускоряться.
|
| рШ |
Относительные перемещения ротора отражаются уравнением движе-
j, dА© _ др
J dt
Учитывая, что
dAa> JAco db А dA&
------ =----------- = А©-------,
dt db dt db уравнение движения можно записать так:
Tj • A© -dAcd = АР ■ db.
Интегрируя это уравнение, найдём кинетическую энергию, полученную ротором при его ускорении:
1 ^от
Ay = — Tj • А©2 = J(PT-Pn(5))-d5.
2 s0
Кинетическая энергия, приобретённая ротором в процессе ускорения численно равна заштрихованной на графике площадке /у, которая получила название площадки ускорения.
После отключения КЗ генератор будет отдавать в сеть мощность большую, чем он получает от турбины (точка 3 на характеристике после- аварийного режима Ри]). Ротор начнёт тормозиться, теряя приобретённую им кинетическую энергию и скорость. Энергия торможения будет равна:
.
At=-Tj-A(o2 = |(рш(5)-/>т)-б/5.
2 8от
Она представлена на рис. 5.7 площадкой торможения /т
В точке 4 относительная скорость ротора А© становится равной 0. Но так как генератор будет по-прежнему отдавать большую мощность, чем он получает от турбины, то в следующий момент его относительная скорость станет меньше 0, и угол 5 начнёт уменьшаться.
Так как принятое математическое описание переходных процессов соответствует позиционной системе, то рассеяния энергии колебаний (избыточной энергии) не будет происходить, и поэтому энергии ускорения и торможения в этом случае будут равны, Ау = Ат. Равны будут и площадки ускорения и торможения.
Максимально возможная площадка торможения /тв в рассматриваемом случае будет ограничена верхней частью характеристики мощности послеаварийного режима Р1П и характеристикой мощности турбины от 80т до 8 кр. Очевидно, что если /тв > /у, то электроэнергетическая система устойчива. Чем больше /тв по сравнению с /у, тем больше запас динамической устойчивости.
5.4. Представление процесса на фазовой плоскости
Для качественного анализа может оказаться полезным рассмотрение зависимости относительной скорости ротора от угла Асо (8) (рис. 5.8). При этом плоскость координат Асо и 8 называется фазовой плоскостью.
В рассматриваемом случае при отсутствии рассеяния энергии колебаний характеристика Асо (8) имеет вид замкнутой кривой, а характер процесса во времени 8(t) представляет собой незатухающие колебания.
В действительности имеет место рассеяние энергии колебаний, и характеристика Асо (8) будет иметь форму спирали, скручивающейся к точке, отвечающей новому установившемуся режиму, а процесс во времени - затухающие колебания.
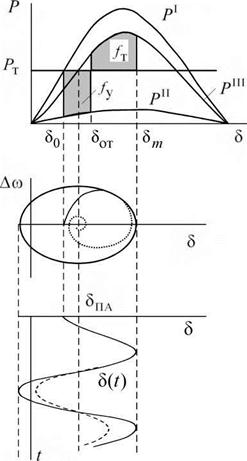 Рис. 5.8. Фазовая и временная переходные характеристики
Рис. 5.8. Фазовая и временная переходные характеристики
|
5.5. Динамическая устойчивость сложной электроэнергетической системы
Расчёты динамической устойчивости выполняются либо на стадии проектирования развития той или иной части ЭЭС, либо на стадии эксплуатации ЭЭС. В первом случае расчёты устойчивости выполняются проектными организациями с целью выбора наилучшего варианта развития ЭЭС, обладающего требуемым запасом устойчивости. При этом одновременно выбираются и средства противоаварийной автоматики. Границ энергопредприятий, как правило, не придерживаются. Схема берётся такого размера, который позволит правильно решить все вопросы. Во втором случае расчёты устойчивости выполняются системным оператором. При этом расчётные схемы составляются для операционных зон каждого ОДУ с присоединением специально рассчитанных эквивалентов соседних регионов. Целью выполнения расчётов устойчивости здесь является настройка существующей противоаварийной автоматики для обеспечения устойчивости ЭЭС.
В расчётную схему входят обычно все источники рассматриваемого региона и сети напряжением, как правило, 220 кВ и выше с их нагрузками. Расчётная схема может насчитывать до 3000 узлов и более.
Рассмотрим электроэнергетическую систему, схема замещения которой содержит N узлов. При составлении математического описания переходных процессов в ней для простоты будем считать, что все генераторы (генерирующие блоки) одной станции в расчёте могут быть представлены одним эквивалентным генерирующим блоком. Разобьём все узлы схемы замещения электроэнергетической системы на четыре группы:
1) узлы, близкие к местам приложения возмущающих воздействий, имеющие генерирующие блоки;
2) узлы, достаточно удалённые от мест приложения возмущающих воздействий, имеющие генерирующие блоки;
3) узлы, близкие к местам приложения возмущающих воздействий, имеющие нагрузки;
4) остальные узлы.
Для генерирующих блоков в узлах группы 1) необходимо взять более точные математические модели, учесть действие регуляторов возбуждения и скорости. Поэтому в качестве моделей элементов одного генерирующего блока возьмём уравнения (1.42) - (1.45), (1.72) - (1.78), (1.81) - (1.82).
Для генерирующих блоков в узлах группы 2) возьмём более простые математические модели. Генераторы будем учитывать с помощью (1.52). Действием регуляторов возбуждения и скорости пренебрегаем, считая Е' = const, РТ = const.
Нагрузку каждого узла группы 3) разобьём на две части: «двигательную» и статическую. Первую будем моделировать уравнениями (1.63) с учётом (1.61), (1.62). Вторую представим постоянной проводимостью
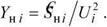
|
Нагрузку каждого узла группы 4), если она есть, представим постоянной проводимостью.
Электрическую сеть в общей модели ЭЭС представим уравнениями узловых напряжений. При этом могут учитываться все активные и реактивные сопротивления и проводимости на землю элементов сети и фактические коэффициенты трансформаций. С учётом принятых моделей генерирующих блоков и нагрузок узлов уравнения узловых напряжений будут выглядеть так:

|
| %1 | Щ | |||
| _ | Уе2 | . | Е\ | (5.4) |
| Ё з | ||||
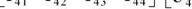
|
Здесь все матрицы блочные. Размерность блоков определяется числом узлов в соответствующей группе узлов. Первая строка относится к группе узлов 1), вторая - к группе узлов 2) и т. д. Блочные матрицы Yek - диагональные. Диагональными элементами этих матриц являются проводимости ветвей, которыми представлены соответствующие генераторы или двигатели в схеме замещения системы. Собственные проводимости узлов Yц
должны включать в себя проводимости ветвей с ЭДС Yej и проводимости
ветвей нагрузок YHi, если соответствующие ветви подключены к узлу i.
Будем считать, что параметры моделей генерирующих блоков в узлах группы 1) в расчёте будут представлены в относительных номинальных единицах соответствующих блоков, а параметры схемы и режима всех остальных элементов системы - в именованных единицах. (Можно было бы принять и другое решение.)
Примем, что все векторные параметры режима элементов сети (напряжения и токи) будут определены в системе координат (qc, dc) угловую скорость которой выберем равной со0, соответствующей частоте 50
Гц. Принятые модели генераторов в узлах группы 2) и модели двигателей определены именно в такой системе координат. Что касается генераторов, подключенных к узлам группы 1), то принятые для них модели определены в системе координат их собственных роторов, которые могут вращаться в переходных режимах с различными скоростями. В связи с этим в расчётах необходимо производить пересчёт некоторых параметров режима генераторов в узлах группы 1) из системы координат (с/, с/) их роторов в
систему координат (qc, dc) и обратно. В рассматриваемом случае пересчитывать необходимо только напряжения и ЭДС генераторов:
(«,/+>л) = С>(/®'; d = {E"q!+jE’d,)h> (5.5)
где Q; — Uj ном ■ с.
Следует помнить, что в принятых моделях в уравнения движения роторов моменты необходимо подставлять в относительных номинальных единицах.
В целом составленная система уравнений, описывающая переходные процессы в сложной ЭЭС, будет подобна (1.86), (1.87).
Для определения параметров установившегося режима, в котором необходимо проверить устойчивость ЭЭС, вначале рассчитывается режим работы электрической сети при заданных, например, узловых потоках мощности и напряжении в базисном узле. Затем, зная напряжения всех узлов сети, определяются параметры режима всех генерирующих блоков и нагрузок. Для этого следует использовать принятые для описания переходных процессов в них уравнения, положив все производные по времени равными 0. Следует использовать также соотношения (5.5).
Задав возмущающее и управляющие воздействия, определяются начальные условия интегрирования. При этом все параметры режима х,
входящие под знак дифференцирования, являются инерционными координатами и в первый момент времени остаются неизменными. Остальные параметры режима у - определяются через них путем решения системы алгебраических уравнений, входящей в (1.86).
Численное интегрирование системы уравнений (1.86), описывающей переходные процессы, часто осуществляется методом Рунге-Кутта четвертого порядка. Расчёт параметров режима на очередном к-м шаге интегрирования продолжительностью At производится в следующей последовательности.
1. 5 = 0.
xi(k) ~ xi(k-\)> i — ■>
Xj — Xj{j, i -\,п,
У j = У j(k-\)’ j = lm.
2. s:= s + 1.
Axi =Fi(xl,...,xn,yl,...,ym)At, i = 1,n;
xi(k) •'= xUk) + a,v - i = l’K.
3. Если s = 4, то перейти к п. 4.
xi = xi(k-\) + fisAxi > i = ln.
Определить yj,j = \,m, решив систему уравнений
ф](х1,...,хп,у1,...,ут) = 0, j = I,т.
Перейти к п. 2.
4. Определить yj(k),j = \,m из системы уравнений
Фj {х\(к)’--->хп(к)’У\(к)’---’Ут(к)) = °- J = l’m-
Здесь а и Р ■ массивы коэффициентов:
а = [1/6, 2/6, 2/6, 1/6], р = [1/2, 1/2, 1].
Так как расчёт одного шага в методе Рунге-Кутта состоит из четырёх
вспомогательных шагов (s = 1,4), то на одном шаге четыре раза необходимо решать систему алгебраических уравнений из (1.86), которая в основном состоит из уравнений узловых напряжений (5.4).
Величина шага интегрирования At зависит от наименьшей постоянной времени из всех элементов системы и может составлять 0,01-^ 0,001 с. Для того чтобы вынести заключение об устойчивости системы, необходимо увидеть, как будут изменяться взаимные углы роторов генераторов 5ij (7) в течение 3 ^ 5 с. Из этого следует, что трудоемкость процесса численного интегрирования очень высока. Затраты времени на численное интегрирование составляют основное время расчётов динамической устойчивости.
Контрольные вопросы
5.1. Динамическая устойчивость ЭЭС. Этапы анализа динамической устойчивости и их характеристика.
5.2. Формирование математической модели ЭЭС для исследования динамической устойчивости.
5.3. Определение начальных условий.
5.4. Что такое возмущающие и управляющие воздействия?
5.5. Как осуществляется наблюдение за переходным режимом ЭЭС?
5.6. По каким параметрам можно сделать заключение о динамической устойчивости большой ЭЭС?
5.7. Энергетические соотношения, характеризующие движение ротора генератора, работающего в простейшей системе. Метод площадей.
6. АСИНХРОННЫЕ РЕЖИМЫ И РЕЗУЛЬТИРУЮЩАЯ УСТОЙЧИВОСТЬ
6.1. Общая характеристика асинхронных режимов
Практически важное значение имеют режимы работы электроэнергетических систем, когда скорости роторов отдельных генераторов отличаются от остальных и их взаимные углы изменяются на 360° и более. Эти генераторы называются работающими асинхронно. Режимы электроэнергетических систем, в которых имеются асинхронно работающие генераторы, называются асинхронными. К таким режимам относятся режимы после нарушения статической или динамической устойчивости отдельных генераторов или групп генераторов, некоторые пусковые режимы генераторов и режимы с АПВ, режимы генераторов при потере возбуждения и др.
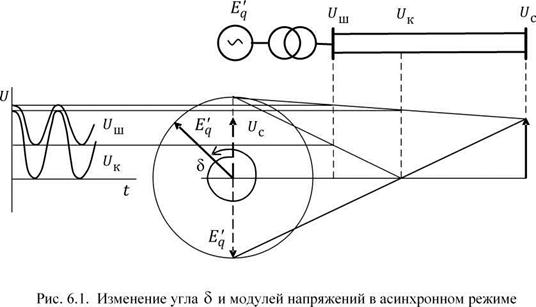
Представим, что в простейшей системе (рис 6.1) генераторы удалённой станции работают асинхронно по отношению к генераторам приёмной части системы. Тогда вектор E'q эквивалентного генератора станции, совпадающий с осью q ротора, будет вращаться по отношению к вектору напряжения Uc шин приёмной части системы со скоростью, пропорциональной скольжению.
|
Угол 8 будет непрерывно нарастать. Слева на рис. 6.1 показано, как будут изменяться модули напряжений на шинах станции и в так называемом центре качаний. Минимальные напряжения в рассматриваемой схеме будут в тот момент, когда вектор E'q займёт положение, противоположное
вектору Uc. В это время в центре качаний величина напряжения станет равной 0, ток генераторов станции будет таким же, как и при трехфазном КЗ в центре качаний. Очевидно, что в случае сложных систем глубокие снижения напряжения, характерные для асинхронных режимов, если это коснется нагрузочных узлов, могут вызвать массовый останов двигателей.
Таким образом, асинхронные режимы - это особые режимы, и допускать тот или иной асинхронный режим можно только после тщательного анализа.
6.2. Возникновение асинхронного режима
Рассмотрим возникновение асинхронного режима в простейшей системе (рис. 6.2) при нарушении динамической устойчивости.
I Uc= const
GKID^---------- а
Рис. 6.2. Схема ЭЭС с приложенным возмущающим воздействием
Предположим, что отключение КЗ произошло недостаточно быстро, и полученный ротором генератора толчок оказался настолько велик, что генератор, ускоряясь, выпал из синхронизма (рис. 6.3).
В начальной стадии процесса скольжение генератора будет достаточно мало, и поэтому анализ процесса можно провести с помощью метода площадей.
После возникновения и отключения короткого замыкания площадка ускорения / оказалась больше площадки торможения /т. Ротор, пройдя участок, где на него действуют тормозящие силы, при 8 > 8кр вновь получает ускорение.
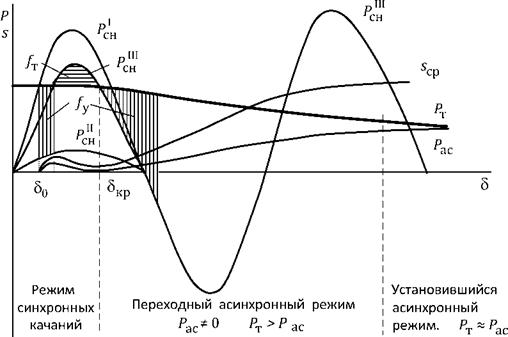 Рис. 6.3. Процесс возникновения асинхронного режима
Рис. 6.3. Процесс возникновения асинхронного режима
|
Поскольку поле статора генератора, созданное внешней системой, вращается со скоростью © 0, то ротор генератора, вращаясь со скоростью
© > ю q, будет пересекать линии поля статора, и в обмотках ротора появятся дополнительные токи с частотой скольжения. Генератор кроме основной синхронной составляющей мощности Рсн начнёт отдавать в сеть дополнительную активную мощность, величина которой будет тем больше, чем больше скольжение. Эту мощность называют асинхронной Рас.
Как только скорость ротора генератора станет больше уставки регулятора скорости турбины, регулятор скорости начнет действовать, уменьшая поступление энергоносителя в турбину. При некоторой скорости вращения ротора мощность турбины и асинхронная мощность генератора уравновесятся. Наступит установившийся асинхронный режим.
Восстановить нормальную работу системы можно быстро, если окажется возможным не отключать выпавший из синхронизма генератор, а заставить его снова войти в синхронизм. При этом говорят, что система сохраняет результирующую устойчивость, так как нарушения энергоснабжения потребителей не произошло.
6.3. Задачи, возникающие при исследовании асинхронных режимов
Допуская в системе асинхронный режим, необходимо проверить как поведение машины, работающей асинхронно, так и поведение остальных машин системы.
Для машины, работающей асинхронно, необходимо проверить допустимость максимальной величины момента (с учетом синхронной и асинхронной составляющей), развиваемого генератором, нагрев обмоток статора и ротора, допустимость напряжения на кольцах ротора (при большом скольжении).
В асинхронном режиме благодаря наличию регуляторов скорости генератор будет отдавать меньшую активную мощность, чем до выпадения из синхронизма. Так как в асинхронном режиме реактивная мощность генераторов обычно велика, то, несмотря на снижение активной мощности, ток статора может стать больше номинального значения и с течением времени вызвать недопустимый нагрев обмоток статора. Обмотки ротора, в которых благодаря скольжению наводятся дополнительные токи, также могут оказаться перегруженными по току. Перегруз по току обмоток статора и ротора будет тем больше, чем больше скольжение ротора генерато-
Асинхронный режим турбогенераторов обычно устанавливается при скольжении порядка десятых долей процента. При этом турбогенераторы могут работать в асинхронном режиме до 15-30 мин в зависимости от системы охлаждения. Скольжение гидрогенераторов в асинхронном режиме больше, чем у турбогенераторов, и поэтому продолжительность асинхронного режима у них более кратковременна - 3 - 4 мин.
Наличие асинхронного режима одной или нескольких машин может оказать влияние на поведение системы в целом. В связи с этим необходимо проверить режим той части системы, которая продолжает синхронную работу. Здесь надо выяснить: не перегрузятся ли генераторы по активной мощности, в связи со сбросом активной мощности асинхронно работающими генераторами, не будет ли недопустимо большого снижения напряжения в узлах нагрузок, что может привести к потере ее устойчивости. Важным также является вопрос о поведении устройств автоматики и релейной защиты, которые без специальной настройки в асинхронных режимах могут работать неправильно.
6.4. Определение параметров асинхронных режимов
Если речь идёт о проверке возможности ресинхронизации генераторов после нарушения устойчивости, допустимости применения АПВ, тех или иных условий пуска генераторов и т. п., то во всех таких случаях задача состоит в расчёте переходного режима электроэнергетической системы и проверке допустимости параметров режима. В целом в этих случаях расчёты переходных режимов аналогичны тем, которые проводятся при исследовании динамической устойчивости. Отличия состоят в требованиях к точности описания переходных процессов в генераторах и двигателях, а также в электрической сети.
Для генераторов, работающих асинхронно, а также для генераторов и двигателей, находящихся сравнительно недалеко (электрически) от асинхронно работающих генераторов желательно использовать полные уравнения Парка-Еорева с учетом насыщения стали и зависимости активных сопротивлений демпферных контуров от скольжения ротора.
Моделирование электрической сети уравнениями узловых напряжений становится менее обоснованным. Элементы матрицы Y уравнений узловых напряжений определяются обычно при номинальной частоте. В асинхронном режиме электрической системы может возникнуть две или более групп генераторов, работающих с разными частотами. Из этой ситуации может быть два выхода:
1. По-прежнему моделирование электрической сети осуществлять уравнениями узловых напряжений и мириться с неизбежными погрешностями. Это может быть приемлемым, если частоты асинхронно работающих групп генераторов отличаются мало (несколько процентов).
2. Каждый элемент электрической сети представлять пофазно дифференциальными уравнениями в мгновенных значениях, которые затем преобразовать, например, в систему координат (d,q, 0). В результате система уравнений, описывающая состояние электроэнергетической системы увеличится на несколько сот (а может быть тысяч) дифференциальных уравнений. Решение задачи значительно усложнится.
Следует отметить еще одну трудность, связанную с расчётом переходного асинхронного режима. Слежение за асинхронным режимом необходимо осуществлять на отрезке времени 10 с и более. Поскольку слежение осуществляется с помощью методов численного интегрирования, то требуется очень большое количество шагов, особенно при учете переходных процессов в статорной цепи, так как шаг интегрирования в этом случае должен быть не более 0,001 с. В любых методах численного интегрирования от шага к шагу накапливается методическая погрешность и, таким образом, чем дольше ведется интегрирование, тем с меньшей точностью определяются параметры режима.
Отдельной задачей является задача определения параметров установившегося асинхронного режима электроэнергетической системы. В теории электрических машин решена задача определения параметров асинхронно
го режима для отдельной электрической машины. Эти результаты можно распространить и на простейшую электроэнергетическую систему (см. рис. 6.2). Для сложных систем предлагается воспользоваться методом наложения (справедливом только для линейных задач). Рассмотрим применение метода наложения для определения момента и мощности генератора, работающего в асинхронном режиме в простейшей системе.
Приближенно считают, что наличие возбуждения не влияет на асинхронную составляющую момента или мощности (не считаются с насыщением стали). Полное значение момента и мощности при этом записывают в виде суммы синхронной и асинхронной составляющих:
М — Мся + Мас, р = р +р
1 1 сн ~ 1 ас •
Ток статора генератора определяют методом наложения (рис 6.4).
Здесь
Z — R + jX; Z0) — R + jX • со *; X-X'd+XBH; Ёа=Ё- со”; Ё = Ё'0; оо*=оо/с
'С00
|
| |||||||||||||
| ||||||||||||||
 | ||||||||||||||
Рис. 6.4. Полная схема замещения системы и схемы замещения для каждого источника
При независимом возбуждении п = 1 ? при наличии возбудителя и подвозбудителя, сидящих на одном валу с генератором, п = 3.
Синхронные составляющие мощности и момента генератора будут равны
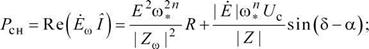
|
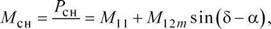 со*
со*
|
R
где а = arctg —.
X
Первое слагаемое синхронной составляющей момента Мп иногда называют собственным моментом, а второе - взаимным. При непрерывном изменении угла 5 значения Мсн и Рси будут изменяться, меняя свою величину и знак. Поэтому их называют знакопеременными составляющи-
При определении асинхронной составляющей момента, развиваемой генератором, приближенно считают, что все три обмотки ротора генератора: обмотка возбуждения, продольная и поперечная демпферные обмотки - равномерно распределены на роторе. Асинхронная составляющая момента генератора от действия трех одноосных обмоток ротора определяется как полусумма моментов от действия трех соответствующих распределенных обмоток. Средняя величина асинхронной составляющей момента при этом будет равна:

|
| М |
| При малых скольжениях полагают |
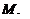
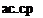 (Г
(Г
 У
У
|
V
Коэффициент Pd называют коэффициентом демпфирования.
Величины сопротивлений и постоянные времени в этих выражениях должны определяться с учетом внешнего сопротивления в цепи статора генератора. При увеличении внешнего сопротивления величина среднего асинхронного момента уменьшается. Типичные зависимости Мас ср
имеют вид, представленный на рис. 6.5.
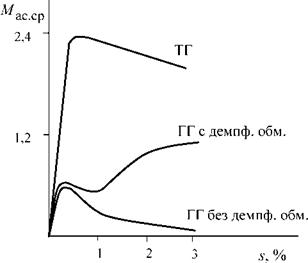 Рис. 6.5. Зависимость среднего асинхронного момента от скольжения
Рис. 6.5. Зависимость среднего асинхронного момента от скольжения
|
Наличие несимметрии (одноосная обмотка возбуждения, явнополюс- ность) приводит к тому, что мгновенная величина асинхронной мощности и момента будет пульсировать около среднего значения. Выражения для мгновенного значения асинхронного момента (и мощности) чрезвычайно громоздки.
6.5. Ресинхронизация генераторов
Рассмотрим процесс ресинхронизации генератора, работающего в асинхронном режиме при скорости больше синхронной в простейшей системе. Наличие возбуждения, а также несимметрии, приводит к тому, что мгновенная величина скольжения асинхронно работающего генератора все время изменяется от некоторого минимального до некоторого максимального значения. Если скольжение станет равным 0, то это будет означать, что генератор в этот момент работает синхронно. Останется или нет генератор в режиме синхронной работы, будет зависеть от соотношения синхронной составляющей момента генератора Мсн и момента турбины Мт в тот момент, когда скольжение стало равным 0 (рис. 6.6).
Если Мсн в момент перехода скольжения через 0 будет больше Мт, то генератор после нескольких циклов качаний станет работать синхронно. Значение угла 5СН, при котором возможно втягивание генератора в синхронизм будет тем ближе к 180°, чем меньше момент турбины по отношению к максимальному синхронному моменту генератора.
Итак, условием ресинхронизации будет:
5 = 0, мсн > мт.
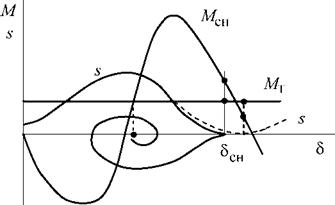 Рис. 6.6. Процесс ресинхронизации генератора
Рис. 6.6. Процесс ресинхронизации генератора
|
Добиться того, чтобы скольжение прошло через 0 можно, во-первых, путем уменьшения момента турбины, от чего уменьшится средняя величина скольжения; во-вторых, увеличивая амплитуду синхронного момента путём увеличения тока возбуждения, от чего увеличится амплитуда колебаний мгновенного скольжения около среднего значения. Необходимые воздействия на турбину оказывает регулятор скорости, а на генератор - регулятор возбуждения. Если асинхронный режим генератора допустим, то ресинхронизация генератора может произойти уже через несколько секунд.
Контрольные вопросы
6.1. Что такое асинхронный режим генератора?
6.2. Как изменяется во времени угол 8, напряжение и активная мощность на выводах генератора в асинхронном режиме? Центр качаний (в простейшей системе).
6.3. Процесс возникновения асинхронного режима в простейшей системе.
6.4. Задачи исследования асинхронных режимов.
6.5. Определение параметров переходного асинхронного режима. Основные трудности.
6.6. Синхронная и асинхронная составляющая мощности (момента) генератора в переходном режиме. Коэффициент демпфирования.
6.7. Процесс ресинхронизации генератора, работающего в простейшей системе.
6.8. Условия ресинхронизации генератора. Как заставить генератор войти в синхронизм?
7. ИЗМЕНЕНИЕ ЧАСТОТЫ И МОЩНОСТИ В ЭНЕРГОСИСТЕМАХ
7.1. Статические характеристики мощности нагрузочных узлов по частоте
Как уже отмечалось, основными потребителями электрической энергии в электроэнергетической системе являются асинхронные двигатели. Мощность, потребляемая асинхронным двигателем для вращения рабочего механизма, согласно Г-образной схеме замещения двигателя, равна
р _ Ujr s_ 0 = —л
г2 +(xs)2 r2+(xs)2
У 1 К 7 (7.1)
со со со-со
х = х0—; X =х0—/ s =------------------------,
со0 со () со
где со 0, со - синхронные угловые скорости вращения роторов генераторов
системы, соответствующие номинальной /0 и произвольной / частотам;
сор- угловая скорость вращения ротора двигателя; х0,х^0 - суммарное
сопротивление рассеяния и сопротивление ветви намагничивания двигателя при номинальной частоте соответственно.
Задавшись каким-либо значением частоты в системе и приравнивая электрическую мощность двигателя мощности механизма
ч!и =Р (s)
2 / \2 JMexVJ/’
Г + (ХЛ')
можно найти скольжение двигателя, а затем по выражению (7.1) активную и реактивную мощности двигателя. Задаваясь различными значениями частоты, можно построить зависимость мощности «асинхронной» нагрузки от частоты (рис. 7.1). Поскольку доля «асинхронной» нагрузки в каждом узле сети велика, то похожий вид имеют и статические характеристики мощности всей комплексной нагрузки в каждом узле.
P(f)
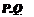
 QCf)
QCf)
/о /
Рис. 7.1. Статические характеристики мощности асинхронной нагрузки по частоте
 |
Получить аналитические выражения характеристик мощности комплексных нагрузок практически невозможно. Поэтому в качестве характеристик мощности комплексных нагрузок по частоте обычно берут уравнения касательных в рабочей точке

|
£н=£но + ^ Д/ = е„о(1-ЧЛ/),
df о
где bHp, bHq - составляющие регулирующего эффекта нагрузки по частоте. При этом Ьнр и 1 %, Ьщ «2 % на 1 % изменения частоты; Ри0, £>н0 - мощности нагрузки в исходном режиме при номинальной частоте.
7.2. Статические характеристики мощности генерирующих
узлов по частоте
Статические характеристики мощности генерирующих узлов по частоте определяются в основном характеристиками мощности турбин и их систем регулирования скорости. Как отмечалось в п. 1.5, зависимость мощности, развиваемой турбиной, при постоянном положении задвижки близка к квадратичной. Для тепловых блоков надо считаться также с тем, что при снижении частоты производительность механизмов собственных нужд будет снижаться. Поэтому результирующая зависимость мощности
турбины от частоты при постоянном положении задвижки будет более сложной (рис. 7.2). Пунктиром на рисунке показана статическая характеристика мощности тепловой турбины с учётом производительности собственных нужд блока.
 Рис. 7.2. Характеристики мощности нерегулируемой турбины:
— без учёта и--------- с учётом производительности собственных нужд
Рис. 7.2. Характеристики мощности нерегулируемой турбины:
— без учёта и--------- с учётом производительности собственных нужд
|
Для каждого положения задвижки будет своя характеристика мощности. Поэтому множество всех режимов работы турбины будет определяться семейством статических характеристик мощности (рис. 7.3).
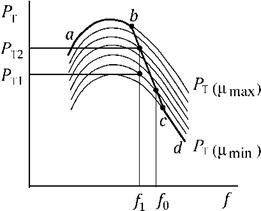 Рис. 7.3. Семейство характеристик мощности при изменении положения задвижки
Рис. 7.3. Семейство характеристик мощности при изменении положения задвижки
|
Наличие регулятора скорости турбины приводит к тому, что при изменении частоты от /0 до f\ турбина будет развивать мощность не Рт1,
а Рт 2- Поэтому эквивалентной статической характеристикой мощности
регулируемой турбины будет кривая abed. В диапазоне регулирования
(участок be) статическая характеристика мощности будет описываться выражением, аналогичным (1.84).
Рт = Рт0 - Рт ном Ьтр А/, (7.3)
где Рт0 - мощность турбины в исходном режиме; Ьтр - коэффициент усиления системы регулирования скорости.
7.3. Баланс мощности в системе при изменении частоты
 При рассмотрении вопросов, связанных с изменением частоты и балансов мощности в системе, используются зависимости, аналогичные рассмотренным выше, в которых все величины следует брать для системы в целом. Электроэнергетическую систему при этом можно представить так, как показано на рис. 7.4.
При рассмотрении вопросов, связанных с изменением частоты и балансов мощности в системе, используются зависимости, аналогичные рассмотренным выше, в которых все величины следует брать для системы в целом. Электроэнергетическую систему при этом можно представить так, как показано на рис. 7.4.
| Tv./) | ■* НС | я (/) | 1, | |
| ^ 1 | 1 |
| 0. |
| Рис. 7.4. Модель электроэнергетической системы |
Баланс мощности при произвольном значении частоты в системе будет выглядеть так:
^то — ^т ном ЬТр А/ = -Рнсо (l + bp А/"), (7-4)
, _ КрРъО + Кпо. D D
р ~ р ’ нсО — нО ^ 0 '
^нсО
Здесь Рт0, Рн0,7Г0 - суммарная генерация в системе, сумма мощностей
нагрузок и потери мощности в сети в исходном режиме соответственно; Рт ном - сумма номинальных мощностей включённых генераторов; Ьтр
- результирующий коэффициент усиления регуляторов скорости;
bHp, bn - регулирующие эффекты по частоте суммарной нагрузки и потерь мощности.
Величины Ьтр, Ьнр определяются как средневзвешенные значения соответствующих элементов системы:
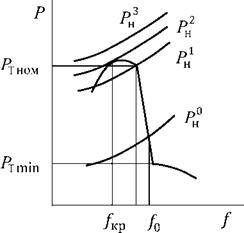
Рис. 7.5. Увеличение мощности нагрузки системы, приводящее к лавине частоты
 ГТ1 T.S / Р]
ГТ1 T.S / Р] ^АРЧ/ ном /, ^^АРЧ / ^1
^АРЧ/ ном /, ^^АРЧ / ^1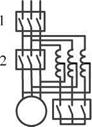

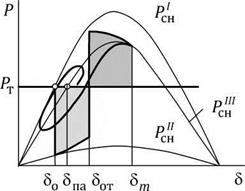 Рис. 9.2. Влияние демпферных обмоток на мощность генератора в переходном режиме
Рис. 9.2. Влияние демпферных обмоток на мощность генератора в переходном режиме
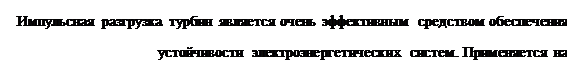
 Рис. 9.3. Импульсное регулирование турбины
Рис. 9.3. Импульсное регулирование турбины
 2
2