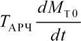КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Dt п dt п dt п dt
|
|
|
|
Здесь тп - число пар полюсов генератора.
В электрическом движении (1.23) будет выглядеть так:
J — = МТ-М, (1.24)
dt 1
где J = J/т^, Мт = Mjjm^, М = М/тп, т.е. генератор с числом пар полюсов тп и скоростью вращения Q заменён генератором с одной парой полюсов и скоростью вращения со.
При расчётах устойчивости электрических систем часто рассматривают не абсолютные движения роторов - по отношению к неподвижной системе координат, а относительные - по отношению к единой системе координат (dc,qc), вращающейся со скоростью сос (рис. 1.7). Эту систему
координат будем называть системными осями. Обычно принимается, что
® с = со о ♦ При этом ю0 = 2л/0 = 3 14 рад/с или ю0= 360°/0 = 18000 эл.град/с, где /0 =50 Гц - номинальная частота.
 Рис. 1.7. Положение ротора в относительном движении
Рис. 1.7. Положение ротора в относительном движении
|
 Очевидно, что относительная А со и абсолютная со скорости ротора, а также его ускорение а будут равны:
Очевидно, что относительная А со и абсолютная со скорости ротора, а также его ускорение а будут равны:
А со = со-со0 =
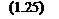 db
db
о-------------------------- = со о + Асо = со о ч;
dt
d со d Acd d2b
a =
dt dt dt2 В относительных единицах соотношения (1.25) выглядят так:
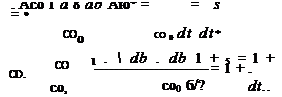 | ||||||||
| ||||||||
| ||||||||
 | ||||||||
| ||||||||
Мощность и момент связаны между собой соотношением
Р = Q М = со М.
В системе относительных единиц при указанном в п. 1.1.2 выборе базисных количеств
Р* = а>*М*. (1-27)
Уравнение абсолютного движения ротора (1.24) в относительных единицах с учетом обозначений (1.26), (1.27) примет вид:
d со*
ГЛ—= MT,-Af,. (1.28)
J 2
Здесь 7>,=<d07>. Tj=-^~, с.
о б
Величина Tj, имеющая размерность времени, называется постоянной инерции. Постоянная инерции численно равна времени разгона?разг ротора отключённого от сети генератора (М* = 0) от состояния покоя (ю * = 0) до номинальной скорости вращения (со* = 1) при приложении номинального момента турбины (Мт* =1). Это следует из (1.28).
со* =1 ^разг*
J* Рj * J* d/*.
о*—0 4=0
Отсюда, учитывая, что ю * = со/со 0, получим Tj = tpa3T.
В справочной литературе для определения Tj обычно приводится так
2 2
называемый маховый момент GD, т • м, при этом в секундах Т = 2,74 GZ)2 - я2 1Q-6
J s6
где п - скорость ротора, об/мин; S6 - базисная мощность, МВ-А. Умножив уравнение (1.28) на со*, можно перейти к мощностям
d ю*
TJ% ®* —— = РТ*~Р*. (1-29)
(Л I г;г
Уравнение относительного движения ротора получается из (1.28) путем соответствующей замены ускорения из (1.26), например,
d Лю,
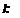 Т
Т
 d t, Tj dh
d t, Tj dh
ffln dt
Если скорость ротора в переходном режиме несущественно отличается от со 0- (менее ~ 4 %), то со* = со/ю0 «1 и, учитывая (1.27), можно принять Д = М*. Это позволяет уравнение относительного движения ротора записать в приближенной форме:
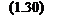 Tj dZb
Tj dZb
Р - Р
2 ± х* * •
й(1 dt
Несмотря на принятое допущение, у этого уравнения имеется широкая область применения. Его можно использовать как для анализа статической, так и для анализа синхронной динамической устойчивости, т. к. при этом скорости роторов генераторов обычно близки к со 0.
Таблица 1.1. Формы записи уравнения относительного движения ротора
|
| |||||||
| |||||||
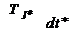 |
| ||||||
| |||||||
Уравнения напряжений обмоток статора в осях d,q: 'd\fd
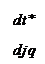
 -ud-to.\[q-idr\ = -uq +ю* \ifd -iqr.
-ud-to.\[q-idr\ = -uq +ю* \ifd -iqr.
Уравнения напряжений обмоток ротора в осях d,q\
d\\i f
—— = uf ~ifrf; dt *
 d\yD
d\yD
 lD rD ’
lD rD ’
£--j Г ~ lQrQ-
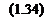 Результирующие потокосцепления обмоток статора: 'I'd' = xd hi + xad if + xad b 5
Результирующие потокосцепления обмоток статора: 'I'd' = xd hi + xad if + xad b 5
tyq — Xq Iq + Xaq Iq.
Результирующие потокосцепления обмоток ротора:
V/ = Xad ld+Xflf+XaJ < \|>D = xad ld + Xad lf + XD lD ’
 \|/^2 — Xaq lq + Xq Iq.
\|/^2 — Xaq lq + Xq Iq.
Уравнения для нулевых составляющих:
 (1.36)
(1.36)
Уравнения (1.31)-(1.36) представляют собою наиболее точную математическую модель генератора. В общей схеме замещения системы генератор в этом случае представляется источником тока (рис. 1.8). Изменение тока источника в переходном режиме определяется указанной выше системой уравнений.
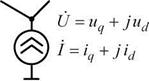 Рис. 1.8. Представление генератора в схеме замещения системы
Рис. 1.8. Представление генератора в схеме замещения системы
|
1.1.6. Модели генератора, не учитывающие электромагнитную инерцию обмоток статора
При исследовании устойчивости электрических систем уравнения Парка-Горева для генераторов, как правило, стремятся упростить, отбрасывая те факторы, которые в определённых условиях не оказывают существенного влияния на движение их роторов. Прежде всего, не учитывают электромагнитную инерцию обмоток статора генератора, пренебрегая в
d \i/ j d \|/„
уравнениях (1.32) трансформаторными ЭДС (считая ------- — = 0, ----- ^ = 0),
dt dt
а также ЭДС скольжения (полагая ю = со 0* = 1). Не учитывают также активные сопротивления обмоток статора генератора, которые довольно ма
лы. При таких допущениях уравнения напряжений обмоток статора генератора примут вид:
Ч= Vd>'
Ud=-Vq>
и в целом описание переходных электромеханических процессов в генераторе будет выглядеть в виде системы уравнений (1.37) - (1.39):
, d(£>s
MT — M;
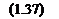
 1j* d v|//
1j* d v|//


 djQ
djQ
= -rQiQ\
|
| ~ud | X X a i | V | ||
| i X a i | Jo_ |
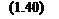
 Решим (1.38) и (1.39) относительно токов:
Решим (1.38) и (1.39) относительно токов:
| id | SX* a b | Uq | ||
| if | — | O ’.Г b | Vff | |
| Jd _ | Q О Q Q О | yD_ |
| V | " \ | b aq | ~ud | ||
| Jq_ | ~Ьад | \ _ | Vo |
Подставляя выражения токов if,iD,iQ в систему уравнений (1.37), получим
 | |||||||||
| |||||||||
| |||||||||
 | |||||||||
| |||||||||
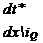 ( bfD^Vf D ^aD uq ) ^D’
( bfD^Vf D ^aD uq ) ^D’
dt ={-bQVo+baoUd)rQ-
Расчётную величину
 | |||||||
| |||||||
| |||||||
называют вынужденной составляющей ЭДС возбуждения Eq.
Величины
X"d=llbd> X"q=ybq получили название сверхпереходных сопротивлений в продольной и поперечной осях. Они не равны друг другу даже для турбогенераторов, но сами величины и их различия достаточно малы. Стремясь к симметричной модели генератора, полагают, что сверхпереходные сопротивления в продольной и поперечной осях одинаковы и равны
x"d + х"
гг _ a q
Это ещё одно допущение, влияющее на точность определения электромагнитных параметров генератора в переходном режиме.
Первые равенства (1.40), (1.41) теперь можно записать в комплексной форме, имеющей вид закона Ома:
(Eq + JE"d) = (Ч/ + JUd) + jX”(}q + j*d)>
где
 E'q = x"baf^f+X"baD^D’'
E'q = x"baf^f+X"baD^D’'
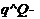 E"d = ~X"bc
E"d = ~X"bc
Величина Ё" = E"q + jE"d получила название сверхпереходной ЭДС. Электромагнитный момент генератора можно определить так
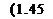
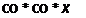 {E'dt,,-E"qud\
{E'dt,,-E"qud\
Таким образом, при принятых допущениях (не учёте трансформаторных ЭДС и ЭДС скольжения, активных сопротивлений обмоток статора и неравенства сверхпереходных сопротивлений в продольной и в поперечной осях) генератор в общей схеме замещения системы должен быть пред-
ставлен ветвью с сопротивлением jx" и приложенной за ним ЭДС Е"
(рис. 1.9). При этом переходные электромеханические процессы в генера-
торе, определяющие изменение Ё", описываются системой уравнений
(1.42) с учетом (1.44), (1.45).
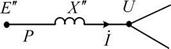 Рис. 1.9. Замещение генератора ЭДС Е"
Рис. 1.9. Замещение генератора ЭДС Е"
|
1.1.7. Модели генератора, не учитывающие электромагнитную инерцию обмоток статора и демпферные
обмотки
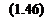 Дальнейшее упрощение уравнений синхронного генератора связано с не учётом демпферных обмоток в продольной и в поперечной осях ротора. Из уравнений (1.37) - (1.39) при этом получим:
Дальнейшее упрощение уравнений синхронного генератора связано с не учётом демпферных обмоток в продольной и в поперечной осях ротора. Из уравнений (1.37) - (1.39) при этом получим:
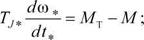 d\\if
d\\if
|
 uq Xd hi xad\f » ud ~ ~xqlq ’
uq Xd hi xad\f » ud ~ ~xqlq ’
|
'I'/ = xad 'ld + V/ '
Уравнение, описывающее переходные процессы в обмотке возбуждения (второе уравнение в (1.46)), можно представить так:
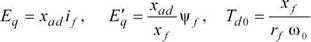 Введены величины
Введены величины
(1.47)
которые получили следующие названия:
Eq - ЭДС холостого хода или ЭДС возбуждения (пропорциональна
полному току обмотки возбуждения);
E'q - переходная ЭДС по оси q (пропорциональна результирующему потокосцеплению обмотки возбуждения по оси q);
Td0 - постоянная времени обмотки возбуждения.
С учётом введенных обозначений (1.47), а также (1.43) систему уравнений (1.46) записывают так:
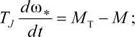
|
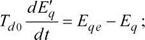
|
(1.48)
Eq — Eg ~ (xd ~ xd ) ’ Uq ~ Eq + %d *d ’
Ud ~ ~Xq lq ’

|
где x'd=xd-^- xf
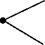
Для неявнополюсных генераторов xq ~ xd, поэтому из 4-го и 5-го
уравнений системы (1.48) вытекает схема замещения неявнополюсного генератора, приведённая на рис. 1.10.
|
| Xd I и -ГПГ\ ___ |
Рис. 1.10. Замещение неявнополюсного генератора ЭДС Е
Изменение Eq в переходном режиме при принятых допущениях описывается уравнениями:
Тг^± = Мт-М;
dt
dE'
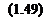 Т7 Ч — Z7 Z7.
Т7 Ч — Z7 Z7.
dQ dt ~ qe q ’
Eq = E'q-(xd-x'd)id’ M = Eqiq/(о*.
У явнополюсных генераторов xd Ф xq. Для них вводится фиктивная ЭДС Eq за сопротивлением xq (рис. 1.11).
Eg Р X I U

|
| -ППП----- |
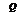 Рис. 1.11. Замещение явнополюсного генератора ЭДС Е{
Рис. 1.11. Замещение явнополюсного генератора ЭДС Е{
 Система уравнений (1.49) в связи с этим преобразуется к виду:
Система уравнений (1.49) в связи с этим преобразуется к виду:
dt

 dE'
dE'
Нужно отметить, что система уравнений (1.50) является более общей, так как при xd = xq из неё получается (1.49).
Следует отметить также, что схемы замещения, приведённые на рис. 1.10, 1.11, для установившихся режимов являются точными.
Величина ЭДС E'q, пропорциональная, как следует из (1.47), результирующему потокосцеплению обмотки возбуждения, в переходном режиме изменяется мало. В определенных условиях можно принять, что в течение всего переходного режима величина E'q остаётся постоянной и равной
своему значению E'q{) до момента нарушения режима. При этом из системы уравнений (1.50) следует:
 lL<to = p_p. dt2 Т ’
lL<to = p_p. dt2 Т ’
EQ=E'q0-(Xq-X'd)id-
Для неявнополюсного генератора в (1.51) вместо xq следует взять xd (при этом Eq будет равна Eq).
Модели генератора (1.46), (1.48)-(1.51) неудобны для расчётов переходных режимов сложных электрических системах. Мешает наличие тока id. Это является следствием одноосной обмотки возбуждения. Стремясь к симметричной модели генератора, вводят расчётную ЭДС Е' (рис. 1.12), как некоторый потенциал за сопротивлением x'd, величину которой в течение переходного режима считают постоянной.
I j
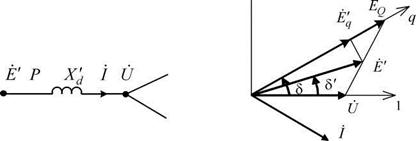 Рис. 1.12. Замещение генератора ЭДС Е'
Рис. 1.12. Замещение генератора ЭДС Е'
|
Переходные процессы в генераторе приближенно учитывают так:

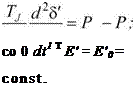 (1.52)
(1.52)
Уравнения (1.52) применяются для моделирования генераторов, удалённых от места возмущения, у которых изменения электромагнитных параметров в переходном режиме достаточно малы.
Если изменением скорости вращения ротора генератора в переходном режиме электрической системы также можно пренебречь, то генератор может быть представлен схемой замещения, приведённой на рис. 1.12, с постоянной по величине и фазе ЭДС Е' = EqZ8'0.
1.2. Описание переходных процессов в нагрузках
Нагрузки узлов электроэнергетических систем при исследовании устойчивости могут учитываться различными способами в зависимости от поставленной задачи и от требуемой точности её решения. При этом вся комплексная нагрузка какого-либо узла или её части могут замещаться эквивалентным синхронным или асинхронным двигателем, учитываться динамическими характеристиками или постоянным сопротивлением.
1.2.1. Описание переходных процессов в синхронных двигателях
Наиболее точным описанием переходных процессов в синхронном двигателе, как и для генератора, являются уравнения Парка-Fорева.
____ U
 М
Рис. 1.13. Положительное направление тока и моменты, приложенные к ротору двигателя
М
Рис. 1.13. Положительное направление тока и моменты, приложенные к ротору двигателя
|
Учитывая, что двигатель в отличие от генератора потребляет электрическую энергию и момент, развиваемый двигателем, является вращающим моментом (рис. 1.13), уравнения для двигателя записывают в виде системы (1.53)-(1.56):
- уравнения напряжений обмоток двигателя
 (1.53)
(1.53)
dyVj
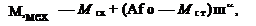 | |||
| |||
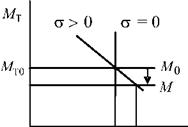
где Мст-момент сопротивления механизма при скорости со = 0 (статический момент); М0 - момент сопротивления механизма при номинальной скорости вращения со0; а - коэффициент, обычно равный 0 н- 2.
Полные уравнения Парка-Горева для описания переходных процессов в синхронных двигателях при исследовании устойчивости электрических систем применяются редко. Обычно используются упрощённые уравнения. Упрощение уравнений Парка-Горева для синхронного двигателя осуществляется точно так же, как и для синхронного генератора. При этом, как и для синхронного генератора, для синхронного двигателя имеется несколько математических моделей, характеризующихся различной степенью точности описания переходных процессов.
1.2.2. Описание переходных процессов в асинхронных двигателях
При анализе переходных процессов больших ЭЭС уравнения Парка- Горева для асинхронных двигателей обычно записываются либо в проекциях на систему координат, вращающуюся со скоростью со 0, либо в проекциях на систему координат, ось q которой совмещена с вектором напряжения узла сети, к которому подключен двигатель. В последнем случае в расчёте появляется много систем координат, вращающихся с различными скоростями сош, и возникает необходимость многократных пересчетов параметров режима из одной системы координат в другую. Здесь для асинхронного двигателя будет использоваться система координат, вращающаяся со скоростью со 0. Обычно это общая система координат для ЭЭС
в целом.
Учитывая симметрию асинхронных двигателей по продольной и поперечной осям, уравнения двигателя можно представить так:
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
|
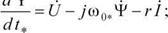

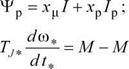

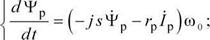

Из двух последних уравнений выразим токи обмоток двигателя:
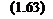 dt
dt
 dE" х„ - х" •
dE" х„ - х" •
С7-
dt хс Т"
 r ХР х" т Х^ ® 0 гр хс Р *с
r ХР х" т Х^ ® 0 гр хс Р *с
М = ту® о* = [E"qUd -E"duq)/x".
Таким образом, при принятых допущениях асинхронный двигатель в схеме замещения системы должен быть представлен ветвью с сопротивлением х" и ЭДС Ё" (рис. 1.14).
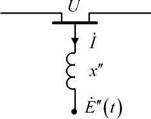 Рис. 1.14. Замещение асинхронного двигателя ЭДС Е"
Рис. 1.14. Замещение асинхронного двигателя ЭДС Е"
|
Изменение Ё" в переходном режиме описывается системой уравнений (1.63).
Модели асинхронного двигателя, не учитывающие переходные электромагнитные процессы. Дальнейшее упрощение уравнений, описывающих переходные процессы в асинхронном двигателе, связано с неучётом переходных электромагнитных процессов и в обмотках ротора. Во втором уравнении системы уравнений (1.63) для этого следует положить dE"/dt = 0. Объединив это уравнение с (1.62), после преобразований получим:
U = ZI:
 | |||||
| |||||
| |||||
Z = jxa+-
+ J'(xap +хц)
где ха, хор - сопротивления рассеяния обмоток статора и ротора.
Эквивалентное сопротивление двигателя Z соответствует схеме замещения, приведённой на рис. 1.15, которая получила название Т- образной.
*ар
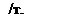 /т
/т
 rv/s
rv/s
Рис. 1.15. Т-образная схема замещения асинхронного двигателя
Таким образом, при принятых допущениях в общей схеме замещения электрической системы асинхронный двигатель должен быть представлен Т-образной схемой, а из уравнений, описывающих переходные процессы в двигателе, осталось только уравнение движения ротора:
T, — = M„PV -M:
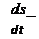
 M = P/&0tt = Re(u2/zy
M = P/&0tt = Re(u2/zy
Определять активную мощность, потребляемую двигателем, по Т- образной схеме замещения достаточно сложно. Так как сопротивление взаимоиндукции хи значительно больше сопротивления рассеяния обмот-
г1
 ки статора ха, то х ставят перед ха и приходят к Г-образной схеме замещения асинхронного двигателя, приведённой на рис. 1.16. Такая схема может быть использована при моделировании всей «асинхронной» нагрузки узла электрической сети.
ки статора ха, то х ставят перед ха и приходят к Г-образной схеме замещения асинхронного двигателя, приведённой на рис. 1.16. Такая схема может быть использована при моделировании всей «асинхронной» нагрузки узла электрической сети.
х
_TYYV
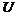
 rp/s
rp/s
Рис. 1.16. Г-образная схема замещения асинхронного двигателя
 В приведённой схеме х = хс+хор. Активная мощность, потребляемая двигателем, необходимая для (1.65), в соответствии с приведённой схемой замещения определяется выражением:
В приведённой схеме х = хс+хор. Активная мощность, потребляемая двигателем, необходимая для (1.65), в соответствии с приведённой схемой замещения определяется выражением:
Р =
rD2 + (s х)2
В переходных режимах ЭЭС напряжения в узлах сети, к которым подключены асинхронные двигатели, могут изменяться значительно. При этом значительно будут изменяться и скольжения роторов двигателей. Сопротивления двигателя хц, х, гр зависят от величины напряжения на обмотках статора и скольжения ротора лд по отношению к вектору напряжения статора, 5Д = s-sv. Изменение индуктивных сопротивлений двигателя объясняется изменением степени насыщения стали. Активное сопротивле
ние обмотки ротора гр зависит от частоты наводимого тока в обмотке ротора. Частота тока зависит от скольжения.уд. Чем больше частота, тем больше гр из-за вытеснения тока к поверхности проводников обмотки ротора.
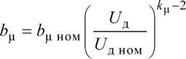 Для Г-образной схемы замещения двигателя изменение хприближённо можно учесть так
Для Г-образной схемы замещения двигателя изменение хприближённо можно учесть так
= W
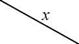
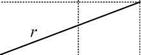
Можно принять к^= 2. При организации расчётов переходных режимов нужна именно - проводимость ветви намагничивания в схеме замещения двигателя. Зависимости х(яд) и гр(5д) представлены на рис. 1.17 в виде кусочно-линейных аппроксимаций [1].
|
X,
Гл
|
р
Рис. 1.17. Зависимости х(зд) и Гр(5д)
Расчётные схемы ЭЭС для анализа переходных режимов, как правило, включают только сети 220 кВ и выше (основная сеть ЭЭС) и насчитывают многие сотни и даже тысячи узлов. В качестве нагрузок в такой схеме фигурируют потоки мощности, уходящие с подстанций основной сети в сети более низкого напряжения, в основном в сети 110 кВ, и далее к множеству конечных потребителей. Поэтому обычно возникает необходимость моде
лировать не один какой-то двигатель (с его рабочим механизмом), а большую группу двигателей, одним эквивалентным, подключенным, например, к шинам 110 кВ основной сети. В [1] приведены следующие параметры эквивалентного асинхронного двигателя для моделирования нагрузок основной сети, о. е.: cosф = 0,8; Мтах=1,7; Мп=0,73; /п = 4,1; £ном=2%;.sр =70%; к^= 4; £3=0,7; МСТ = 0,5; Гу=0,8с-для
кратковременных возмущений; Tj = 0,6 с - если двигатели глубоко тормозятся.
Этим данным соответствуют следующие параметры Г-образной схемы замещения двигателя: х0 =0,368; х1 =0,266; г0 =0,0226;
rj =0,0424; х(Д=2,95.
В целом моделирование асинхронной нагрузки (60-70 % потребления в узле) выполнить точно невозможно. Однако требования к точности моделирования высоки. Ведь расчёты переходных режимов ЭЭС осуществляются с целью обеспечения эффективного противоаварийного управления.
1.2.3. Учёт переходных процессов в комплексных нагрузках с использованием их статических характеристик
Нагрузка в схеме замещения системы представляется ветвью (рис. 1.18) с некоторым сопротивлением хн* = 0,2 ^-0,4, за которым приложена ЭДС Е, изменяющаяся во времени.
U и
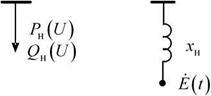 Рис. 1.18. Представление комплексной нагрузки в переходном режиме
Рис. 1.18. Представление комплексной нагрузки в переходном режиме
|
При этом переходные процессы в комплексной нагрузке приближённо учитываются так:
T„- = U-jx„^--E, н dt J н U
где SH = Рн(U) + jQH(U) - мощность нагрузки, учитываемая статическими характеристиками; Ти - постоянная времени, выбираемая из опыта расчётов.
При необходимости можно учесть и зависимость мощности, потребляемой комплексной нагрузкой от частоты:
'PB(U,s) = (l + kPs)Pa(U);
Qn(U,s) = (\-kQs)Qn(U),
дР дО
где кР = ——, к0 = - составляющие регулирующего эффекта
ds ds
нагрузки по частоте; s - скольжение вектора напряжения на шинах нагрузки по отношению к системе координат, вращающейся со скоростью
1.2.4. Учёт нагрузки постоянным сопротивлением
При исследовании устойчивости электроэнергетических систем нагрузки узлов могут замещаться постоянными сопротивлениями, определяемыми по параметрам исходного установившегося режима:
z. -"L
Н I £
/
При этом уменьшается общее количество дифференциальных уравнений, описывающих переходные процессы в системе. Это оправдано для удаленных от места возмущения нагрузок, а также для нагрузок малой мощности.
1.3. Моделирование электрической сети при расчётах устойчивости
При расчётах устойчивости ЭЭС электрическая сеть может содержать от нескольких сот до нескольких тысяч элементов (участков линий, трансформаторов, реакторов, батарей конденсаторов). Учитывая общий объем схемы, большое количество расчётов, необходимых для создания и настройки эффективного противоаварийного управления, несовершенство методов численного интегрирования и имеющийся уровень вычислительной техники, применить для расчётов переходных режимов волновые методы сейчас практически невозможно, да и надо ли? Применяемые в настоящее время программы расчёта переходных режимов основываются на представлении элементов ЭЭС уравнениями и схемами замещения с сосредоточенными параметрами.
Во время переходного режима электрическая система переходит от одного установившегося состояния к другому установившемуся состоянию. При этом изменяется количество энергии, запасённой (связанной) в отдельных элементах системы. Основное количество энергии запасается в виде энергии электромагнитных полей генераторов и двигателей, а также в виде кинетической энергии вращающихся масс. По сравнению с этим энергия, запасаемая в элементах электрической сети, оказывается значительно меньше. Поэтому электрическая сеть в целом не оказывает большого влияния на протекание переходных режимов в ЭЭС. Для учета влияния (электромагнитной инерции) электрической сети потребовалось бы включить в общую систему уравнений, описывающую переходные процессы в ЭЭС, большое количество дифференциальных уравнений с малыми постоянными времени, описывающих переходные процессы в элементах сети. Задача расчёта переходного режима большой ЭЭС значительно бы усложнилась. Исходя из того, что влияние сети на переходные режимы ЭЭС не так уж велико, при расчётах устойчивости ЭЭС электрическую сеть в целом, как правило, считают безынерционным элементом. Состояние сети при этом описывается уравнениями установившегося режима (алгебраическими уравнениями). Например, исходя из метода симметричных составляющих, уравнениями узловых напряжений.
Нужно отметить, что неучёт электромагнитной инерции электрической сети, а также электромагнитной инерции обмоток статоров генераторов и двигателей приводит к неучёту апериодических составляющих токов в элементах ЭЭС, возникающих в первый момент после нарушения режи-
При использовании метода симметричных составляющих необходимо составлять три системы уравнений в комплексных переменных - для токов прямой, обратной и нулевой последовательностей. Но, во-первых, расчёт токов нулевой последовательности при расчётах устойчивости не нужен, так как токи нулевой последовательности не участвуют в создании электромагнитных моментов генераторов и двигателей. Во-вторых, токи обратной последовательности приводят к появлению дополнительных составляющих моментов электрических машин, пульсирующих с двойной частотой. Тяжелые роторы не могут так быстро менять свою скорость и реагируют практически только на средние значения этих моментов, которые малы. Нужно учесть также, что токи обратной и нулевой последовательности возникают при появлении несимметрии в схеме, например, из-за несимметричного повреждения какого-либо её элемента. После устранения причины несимметрии (отключение поврежденного элемента) в схеме будут протекать только токи прямой последовательности.
Учитывая сказанное, при расчётах устойчивости электрическая сеть с определенными допущениями может моделироваться уравнениями узловых напряжений, составленными по комплексной схеме замещения для токов прямой последовательности. Нужно отметить, что при использовании
метода симметричных составляющих рассматривается только гармоника с частотой ю0.
1.4. Описание переходных процессов в системах возбуждения генераторов
Система возбуждения генератора состоит из возбудителя, подвозбу- дителя и автоматического регулятора (АРВ). В нормальных режимах задача регулятора состоит в поддержании требуемой величины напряжения в заданной точке схемы, а в переходных режимах действие регулятора должно также способствовать затуханию возникших колебаний.
Применяемые на генераторах в настоящее время регуляторы возбуждения в основном разделяются на регуляторы пропорционального типа и регуляторы сильного действия. Регуляторы пропорционального типа изменяют ток возбуждения генератора пропорционально отклонению регулируемого напряжения. Регуляторы сильного действия реагируют не только на отклонение регулируемого напряжения, но и на отклонения других параметров режима, а также на производные параметров режима.
1.4.1. Структурная схема и описание переходных процессов
в системах регулирования возбуждения пропорционального
типа
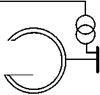 Структурная схема системы регулирования возбуждения пропорционального типа представлена на рис. 1.19.
Структурная схема системы регулирования возбуждения пропорционального типа представлена на рис. 1.19.
I ^ Т/го
| 1—* иг\ | ■ Кои | AUT | | Ае | ||
| 1 + рТи | \ + рТр | \ е0— | 1 + рТе |
| АРВ Возбудитель Генератор |
| Рис. 1.19. Структурная схема системы регулирования возбуждения пропорционального типа |
Переходные процессы в системе регулирования возбуждения пропорционального типа могут быть учтены следующим образом (учитывая
(1.43)):
-в возбудителе
J_
1+ рТе
-в регуляторе
Ае = ^ A Ur, (1.69)
(l + pTpXl + pTu)
где Те, Тр, Tjj - постоянные времени возбудителя, усилительного и измерительного элементов регулятора; A UT = Ur0 -UT - отклонение регулируемого напряжения UT от требуемого уровня Ur0; Кои - общий коэффициент усиления системы регулирования возбуждения по отклонению напряжения.
Подставляя (1.69) в (1.68), можно получить общее уравнение, отражающее переходные процессы в системе регулирования возбуждения пропорционального типа
Л J- ^0 и А тт
А Еае =------------------------------------- A UT.
(i+pTvXi + pTyXi + pTj
В установившемся режиме (р — 0)
~ Kqu ' ^ Ur,
т. е. добавка к вынужденной составляющей ЭДС холостого хода Eqe пропорциональна отклонению A UT регулируемого напряжения от требуемого уровня.
Коэффициент усиления по отклонению напряжения системы регулирования возбуждения имеет следующую размерность
v _ ^Eqe ед.возб.
0 U ~ А Тт ’ ’
А иг ед.напр. что читается как «единиц возбуждения на единицу напряжения».
В качестве единицы напряжения принимается номинальное напряжение генератора. В качестве единицы возбуждения служит величина Eqe
либо в режиме холостого хода генератора (равна номинальному напряжению генератора), либо в режиме номинальной нагрузки генератора. В первом случае размерностью коэффициента усиления по отклонению напряжения будет ед.возб.хх/ед.напр, во втором ед.возб.ном/ед.напр.
Для того чтобы величина A UT была незначительной, необходимо обеспечить очень большой коэффициент усиления по отклонению напряжения. Приближенно можно считать, что
дс/г, = _^1_* _L.
Uг ном Kqu
Таким образом, если потребовать точность поддержания напряжения А итш = (1 -г- 2) %, то необходимо иметь = (50^-100) ед.возб.хх/
ед.напр. Столь большая необходимая величина коэффициента усиления по отклонению напряжения приводит к тому, что система возбуждения генератора с регуляторами пропорционального типа оказывается неустойчивой. В системе возбуждения возникают колебания с нарастающей амплитудой. Системы возбуждения с регуляторами пропорционального типа устойчиво могут работать с Кои < 10, и поддержание напряжения генератора часто оказывается неудовлетворительным.
1.4.2. Структурная схема и описание переходных процессов
в системе регулирования возбуждения сильного действия
Поиски путей обеспечения устойчивой работы электроэнергетических систем при больших коэффициентах усиления по отклонению регулируемого напряжения привели к созданию так называемых систем возбуждения сильного действия. Оказалось необходимым вести регулирование возбуждения не по одному, а по нескольким параметрам регулирования и не только по отклонениям, но и по производным параметров регулирования, иметь практически безынерционные возбудители («0,05 с) с высоким потолком возбуждения, (2 н- 4) uf ном.
Структурная схема системы регулирования возбуждения сильного действия приведена на рис 1.20.
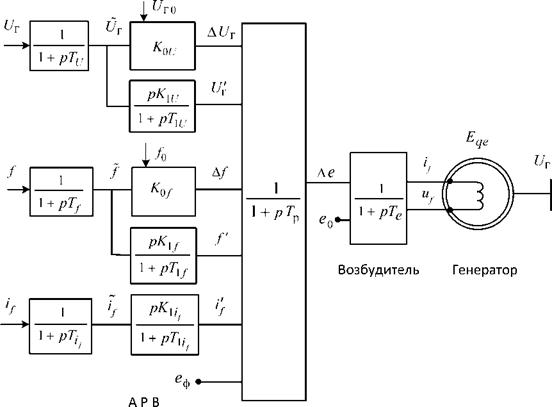 Рис. 1.20. Структурная схема системы регулирования возбуждения сильного действия
Рис. 1.20. Структурная схема системы регулирования возбуждения сильного действия
|
Переходные процессы в системе регулирования возбуждения сильного действия в общем виде можно учесть следующей системой уравнений:
- в возбудителе
Д£,е = Же(р).Де; (1.70)
- в регуляторе
Ле = 5>я.(/>)-ЛЯ./, (1.71)
nj '
где We (p) - передаточная функция возбудителя; Wn {р) - передаточная
функция регулятора по каналу параметра регулирования Я ;.
Для реальных устройств передаточные функции We (р), Wn (р)
достаточно сложны. Вид передаточных функций, которые с определенной точностью аппроксимируют истинные, как правило, рекомендуется разработчиками систем регулирования возбуждения. Обычно принимается, что передаточная функция тиристорного возбудителя
We{p) =; (1-72)
ек ’ \ + рТе
передаточная функция регулятора по каналу параметра регулирования /7/
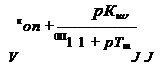 (V \
(V \
 w„Ap)
w„Ap)
(1 + рГр)(1 + ^Гя.
Здесь Коп, Кхп - коэффициенты усиления по отклонению и первой производной параметра 77; те, т тп тш - постоянные времени возбу-
J J J
дителя, усилительного, измерительного и дифференцирующего элементов регулятора соответственно.
При анализе динамической устойчивости электроэнергетических систем используется численное интегрирование. Поэтому операторные уравнения (1.70)-(1.73) приходится записывать в форме обыкновенных дифференциальных уравнений. Необходимо учитывать также важные конструктивные ограничения, проявляющиеся при больших возмущениях.
Дифференциальные уравнения переходных процессов во входных цепях АРВ:
- в канале регулируемого напряжения
dUT
т ____ L - ту _ ту ■
1Ur 7, _ Г UT’
r dt
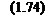 dU'Y
dU'Y
eu=Km(Un-UT) + KwU'T;
в канале частоты
гД = /»-/;
dt
 T4^7 = -f' + ^rd»-f)
T4^7 = -f' + ^rd»-f)
 dt
dt
f
ef=K4(f-f0) + K,}f;
- в канале тока возбуждения

Рис. 1.21. Система регулирования скорости ротора генератора
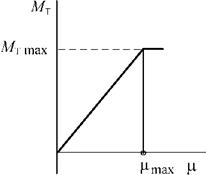 Зависимости момента турбины от положения задвижки и от скорости вращения турбины приведены на рис. 1.22.
Зависимости момента турбины от положения задвижки и от скорости вращения турбины приведены на рис. 1.22.