Рассмотрим модели надёжности невосстанавливаемых элементов. Надёжность невосстанавливаемых элементов характеризуется наработкой между отказами

Модели надёжности для элементов.

Лекция № 2.

Машина состоит из сборочных единиц и систем, которые в свою очередь состоят из элементов. Элементы с точки зрения надёжности бывают:

- восстанавливаемые после отказа

- невосстанавливаемые после отказа.

Автомобиль в целом восстанавливаемый объект, состоящий из сборочных единиц и элементов, часть из которых являются восстанавливаемыми путём ремонта, а часть невосстанавливаемыми.

1. Модели надежности для невосстанавливаемых элементов: модель нестареющих элементов и модель слабого звена

Наработка до отказа представляет собой случайную непрерывную величину.

Вероятность безотказной работы R(x).

R (x)=Р (нет отказа при наработке < х)

R (x) – функция надёжности

F (x) – вероятность отказа

F (x)=1- R (x) – противоположные события.

Если известна функция распределения случайной величины наработки на отказ F (x), то для заданной наработки можно определить вероятность безотказной работы.

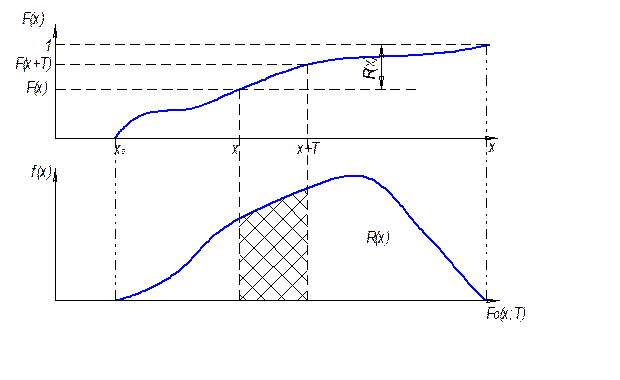
Вероятность отказа F₀ (x; T) за период Т после момента х определяется по формуле:

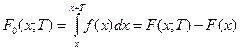
Для удобства вводится величина интенсивности отказов – условная плотность интенсивности отказа:

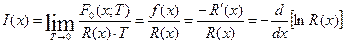
Отсюда: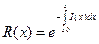- то есть, зная интенсивность отказов можно определить вероятность безотказной работы.

Если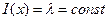

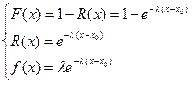
Интенсивность отказов у различных элементов формируется по-разному в зависимости от структуры элементов и физики процесса повреждений.

1. Модель «нестареющих» элементов

Если интенсивность 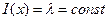- что характерно для «нестареющих» элементов, не изменяющих свои свойства при эксплуатации, вероятность безотказной работы не зависит от предшествующей наработки, а только от Δх:

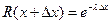
Для таких элементов случайная величина наработки на отказ распределена по экспоненциальному закону:

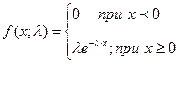
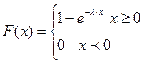
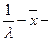средняя наработка на отказ.

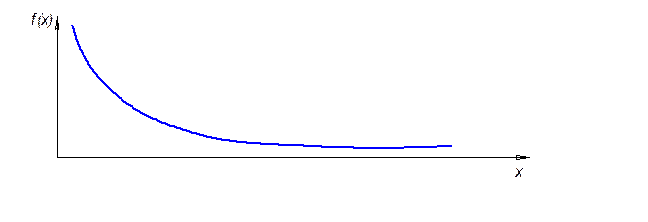
2.Модель «слабого звена»

Если сложный элемент включает группу независимых звеньев, при этом отказ любого из них приводит к отказу сложного элемента, то в такой модели распределение наработки на отказ рассматривается как распределение минимальных значений наработок отдельных звеньев:

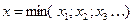
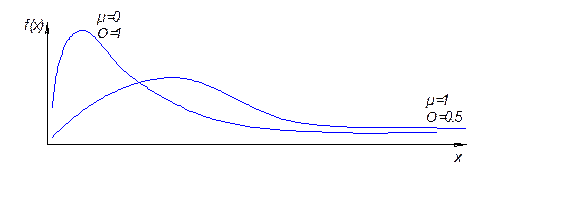
Теоретики (Фишер) доказали, что при достаточно большом числе звеньев в элементе для большинства законов распределений наработки до отказа звеньев распределение наработки элемента будет описываться распределением Вейбулла:

Плотность распределения: 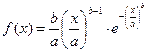, где

а и в – параметры распределения;

а – параметр масштаба;

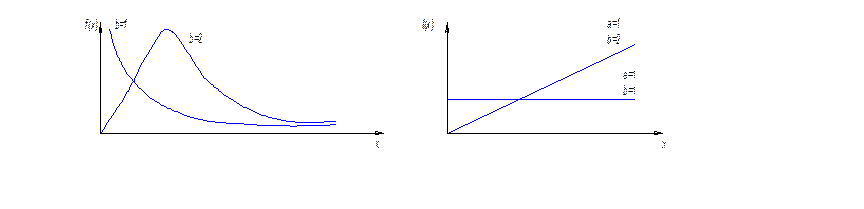
в – параметр формы.

При в=1 – экспоненциальное распределение

1. 6. Модели надежности для невосстанавливаемых элементов: модель пропорционального эффекта и модель резервирования звеньев.

. Модель резервирования звеньев.

Если сложный элемент состоит из звеньев, а отказ элемента происходит при отказе всех звеньев, то функция плотности распределения вероятности отказа сложного элемента представляет собой п-кратную свёртку функций плотного распределения для звеньев.

Если число звеньев не велико, то закон распределения вероятности отказа определить сложно. Однако если наработка для звеньев распределена по экспоненциальному закону, то закон распределения наработки элемента – это гамма-распределение:

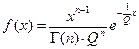, где

п – число звеньев;

Q – параметр масштаба.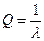

При большом числе элементов закон распределения наработки на отказ элемента асимптотически стремится к нормальному закону со средним значением nQ и дисперсией n²Q². Отсюда видно, что резервирование повышает наработку на отказ пропорционально числу резервных звеньев.

Модель пропорционального эффекта.

Если показатель работоспособности при эксплуатации изменяется от номинального значения до предельного таким образом, что изменение показателя пропорционально достигнутому уровню:

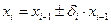
или , где

х₀ – номинальное значение;

х_п – предельное значение;

δ_i – интенсивность изменения.

Закон распределения ресурса определяется законом распределения х_п:

Если прологарифмировать, то

Согласно центральной предельной теореме случайная величина 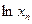имеет нормальное асимптотическое распределение, а сама величина х_п распределена по нормальному логарифмическому закону:

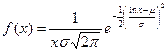
Модель элементов с несколькими видами отказов

При допущениях:

Дата добавления: 2014-01-07